多项式全家桶【长期更新】

目录

• 多项式
  • 定义（表达式）
  • 暴力全家桶
    • 加法
    • 乘法
    • 余数除法
    • 求导和积分
    • 求逆
    • 开根
    • 求对数
    • 求指数
    • 求三角函数
  • 快速傅里叶变换FFT，快速多项式
    • 前置内容
  • FFT
    • 核心思路
    • 具体做法
    • 常数优化：非递归FFT

多项式

定义（表达式）

定义一个 \(n\) 次的多项式为：

\[F(x) = \sum^n_{i=0}f_ix^i \]

注意 :

1. \(i=0\) 的那一项是常数项。
2. 易得\(F(0) = f_0\)
3. 在OI中，多项式一般在同余条件下讨论\(（mod\ p）\)，在下文中会省略 "$\huge\equiv $" 符号。
4. 求多项式\(F(x)\)，实际上就是把每一个\(f_i\)求出来。

暴力全家桶

加法

给定两个多项式 $ F(x) $ 和 $G(x) $，求它们的和 $ H(x) $。
即： $ H(x) = F(x) + G(x) \( \) h_i = f_i + g_i $
（类比高精度加法）
复杂度 $ O(n) $

乘法

即：\(H(x) = F(x)G(x)\)

\[h_i = \sum^i_{j=0}f_jg_{i-j} \]

就是合并同类项

复杂度 \(O(n^2)\)

余数除法

已知F和H，求G和R

即：\(H(x) = F(x)G(x) + R(x)\)

就是小学奥数里的大除法。

\(O(n^2)\)

求导和积分

若：\(G(x) = F'(x)\)
则：\(g_i = (i+1)\times f_{i+1}\)
若：\(H(x) = \int F(x)dx\)
则：\(h_i = \frac{f_{i-1}}{i}\)

求逆

F已知求G。

即：\(F(x)G(x) = 1(mod\ p)\)

\[g_0 = f_0^{-1} (带入x = 0,f_0^{-1}用普通的求逆元的方法即可) \\ \sum^i_{j=0}f_jg_{i-j} = [i=0]\\ f_0g_i = [i=0] - \sum^{i}_{j=1}f_jg_{i-j} \ \text{把第i项单独拿出来}\\ g_i = \frac{[i=0] - \sum^{i}_{j=1}f_jg_{i-j}}{f_0} \]

递推求即可。

\(O(n^2)\)

开根

\(G^2(x) = F(x)\)，已知F求G

\[\sum_{0 \le j \le i} g_jg_{i-j} = f_i\\ 2 g_ig_0 = f_i - \sum_{0 \le j \le i} g_jg_{i-j} \\ \text{就是把第一项和最后一项提出来，类比求逆} g_i = {f_i - \sum_{0 \le j \le i} g_jg_{i-j} \over 2g_0} \]

还是用递推，\(O(n^2)\)

特别的，\(g_0^2 = f_0\) 作为边界情况。

• 若 \(f_0\neq0\)，则 \(G\) 的解数，取决于 \(f_0\) 的平方根数量。（具体参见二次剩余）

• 若 \(f_0=0\)，令 \(F(x)=x^kH(x)\)，满足 \(h(0)\neq0\)，那么若 \(k\) 为奇数，则 \(G\) 无解；若 \(k\) 为偶数，记 \(P^2(x)=H(x)\)，那么 \(G(x)=x^{\frac k2}P(x)\)。

这是因为开跟运算本身不一定有解。

求对数

给定多项式 $ F(x) $，求 $ G(x) \equiv \ln F(x) \pmod{x^n} $，保证 $ f_0 = 1 $。

解：对原等式两边求导，得：

\[G'(x) \equiv F'(x) F^{-1}(x) \pmod{x^n} （复合函数求导）\\ 令 H(x) \equiv F^{-1}(x) \pmod{x^n} （多项式求逆）\\\therefore G'(x) \equiv F'(x) H(x) \pmod{x^n} \\\therefore (i+1)g_{i+1} = \sum_{j=0}^{i} (j+1)f_{j+1}h_{i-j}, g_0 = \ln(f_0) = 0\\\therefore g_i = \frac{\sum_{j=0}^{i-1} (j+1)f_{j+1}h_{i-j-1}}{i} \]

\(O(n^2)\)

求指数

给定多项式 $ F(x) $，求 $ G(x) \equiv e^{F(x)} \pmod{x^n} $，保证 $ f_0 = 0 $。

对原等式两边求导，得：

$ g_0 = e^{f_0} = e^0 = 1 $

\[G'(x) \equiv F'(x)e^{F(x)} \quad \text{(复合函数求导)} \equiv F'(x)G(x) \pmod{x^n} \]

\[\therefore (i+1)g_{i+1} = \sum_{j=0}^{i} (j+1)f_{j+1}g_{i-j} \]

此式子也可看成求对数的第三步和第四步，把F换成G，把G换成F

求 $ g_{i+1} $ 时已求出 $ g_0 $ 到 $ g_i $， 故可以递推求出 $ G(x) $

\(O(n^2)\)

求三角函数

前置知识：[欧拉公式（\(e^{ix}的代换\)）](https://www.cnblogs.com/water-flower/p/18651768#- 定义五：在复数中的定义(欧拉公式)-) ，泰勒展开

由欧拉公式：

\[e^{ix} = \cos x + i\sin x \]

\[e^{-ix} = \cos x - i\sin x \]

两式相加得

\[\cos x = \frac{e^{ix} + e^{-ix}}{2} \]

两式相减得

\[\sin x = \frac{e^{ix} - e^{-ix}}{2i} \]

现在我们把三角函数换成了指数函数，用指数的方法来推导三角函数。

\(O(n^2)\)

快速傅里叶变换FFT，快速多项式

终于进入正题了。

前置内容

1. 多项式插值：n + 1 个点值可确定一个 n 次多项式。

   很好理解。用待定系数法高斯消元。

   系数矩阵满秩，所以不会是无数解。

   有如果无解，说明有两行的系数，上面的系数都是下面的系数的k倍。但是对于不同的x，\(\{x^i\}\) 的集合不会是这种比例关系。

2. 复数运算：参见数学书

3. 单位根
   P.S. 以下为了方便书写，均将 \(\omega\) 简写为 \(w\)，且将 \(\omega_n^i\) 表示为 \(w_i\)。

   定理：任何复系数一元n次多项式方程在复数域上至少有一个根。

   大多数数学家都认为这是对的。

   推论：任何复系数一元 \(n\) 次多项式方程在复数域上恰好有 \(n\) 个根。

   设现有一根 \(x_i\)。

   若将原 n 次多项式因式分解，必定存在一项形如 \((x - x_i)\)。把这一项去掉，得到一个 n-1 次的多项式。而这个新的多项式必有一根。再把这个根去掉。重复这个操作。因为可以降幂 n 次，所以有 n 个根。

   单位根定义：\(x^n−1=0\) 的 \(n\) 个根，记作 \(w_0,w_1...w_{n-1}\)。

   单位根几何意义：建立复数域的坐标系。做单位圆。运算用向量的运算。这里以 \(n=6\) 为例。

   

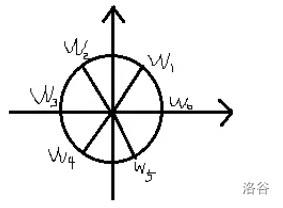
   用三角函数来表达这些单位根可得： \(w_i = \cos{2i\pi\over n} + i\sin{2i\pi\over n}\)

   首先显然有：\(w_{kn+i} = w_i\)，这相当与多转 k 圈。

   通过化简，\((w_i)^2 = (\cos{2i\pi\over n} + i\sin{2i\pi\over n})^2= \cos2{2i\pi\over n} + i\sin2{2i\pi\over n} = w_{2i}\)，这个可以看为把和x轴的夹角翻倍。

   同理（大概是用一些二项式定理和欧拉定理展开后乱搞），\((w_i)^n = w_{in} = w_0\)

   所以一个单位根的 \(n\) 次方都是 \(1 + 0i\)

   下面给出一些关于单位根的运算性质 ：

   • \(w_{i+n}=w_i\)

   • \(w_iw_j=w_{i+j}\)

   • \((w_{i})^j=w_{ij}\) 次方转下标

   • \(-w_i=w_{-i}\)

   • \(w^{ki}_{kn} = w^{i}_{n}\)

     单位根反演

     （应该只在IDFT的证明中有用到）

     这里用 \(w_i\) 代表 \(w_i^n\)

     \[\sum\limits_{i=0}^{n-1}{w_i^k}=n[n\mid k] \]

     证明：

     \[\sum\limits_{i=0}^{n-1}{w_i^k} = \sum\limits_{i=0}^{n-1}{w_k^i} \]

     该式为等比数列，所以：

     \[\sum\limits_{i=0}^{n-1}{w_k^i} = \begin{cases}&n \text{ if } w_k = 1 \\&{1 - w_k^n \over 1 - w_k} \text{ if } w_k != 1 \end{cases} \]

     观察到，\(w_k^n = w_{nk} = 1\)，并且 \(w_k = 1 \Leftrightarrow n|k\)

     所以上式化简为：\(\sum\limits_{i=0}^{n-1}{w_i^k}=n[n\mid k]\)

FFT

这玩意可以做到 \(O(n\log n)\) 的多项式乘法。老牛逼了。

核心思路

根据多项式插值，我们根据 \(F(x)G(x)\) 的 n + 1 个点值，然后用插值法，可以插出这个多项式。

通过优秀的选点（单位根），可以做到 \(O(nlogn)\)。

现在我们有两个要做的事情：

1. DFT：输入一个 \(n-1\) 次多项式的系数列，快速得到其在 \(n\) 次单位根处的点值列，也就是求 \(F(w_i)\)。
2. IDFT：在优秀的时间复杂度内插值出多项式，也就是用 \(H(x_i)\) 去求 \(h_i\)（点值求系数）。

具体做法

先来解决DFT：

\[\begin{align} F(w_i) &= \sum\limits_{i=0}^{n-1}{f_iw_k^i}\\ &= \sum^{\frac n2-1}_{i=0}f_{2i}w_k^{2i} + \sum^{\frac n2-1}_{i=0}f_{2i+1}w_k^{2i+1} \text{把i按照奇偶分组}\\ &= \sum^{\frac n2-1}_{i=0}f_{2i}w_k^{2i} + w_k^1\sum^{\frac n2-1}_{i=0}f_{2i+1}w_k^{2i} \end{align} \]

\[\therefore DFT(F) = \mathrm{DFT}(\{f_0,f_2\dots f_{n-2}\})_k+w_k\mathrm{DFT}(\{f_1,f_3\dots f_{n-1}\})_k\\ F(x) = F1(x) + xF2(x) \]

带入 \(w_k(k < {n \over 2})\)，\(F(w_k) = F1(w_k) + w_kF2(w_k)\)

带入 \(w_{k + {n\over 2}}(k<{n\over 2})\)，\(F(w_k) = \sum\limits^{\frac n2-1}_{i=0}f_{2i}w_{k}^{2i} + w_{k+{n\over 2}}^1\sum\limits^{\frac n2-1}_{i=0}f_{2i+1}w_k^{2i}\)

\(w_{k + {n\over 2}}^{2i} = w_{2k + n}^{i} = w_{2k}^{i} = w_{k}^{2i}\)，\(w_{k+{n\over 2}} = w'_{k}\) 这里 \(w_{k+{n\over 2}}\) 以 \({n\over 2}\) 为底， \(w'_k\) 以 n 为底。

所以带入 \(w_{k + {n\over 2}}(k<{n\over 2})\)，\(F(w_k) = F1(w_k) - w_kF2(w_k)\)

于是可以递归求解。

复杂度是 \(T(n)=2T(\frac n2)+O(n)\) ，是 \(O(n\log n)\) 的

可以发现，DFT能做到高效的原理实际上是利用的单位根的运算性质。

再来看IDTF：

根据单位根反演可以推到出这个公式：

\[nh_k=\sum\limits_{i=0}^{n-1}w_{-k}^iH(x_i) \]

证明：

\[\begin{align} \sum\limits_{i=0}^{n-1}w_{-k}^iH(x_i) &=\sum\limits_{i=0}^{n-1}w_{-k}^i\sum\limits_{j=0}^{n-1}w_{i}^jh_j\\ &=\sum\limits_{j=0}^{n-1}h_j\sum\limits_{i=0}^{n-1}w_{-k}^iw_{i}^j\\ &=\sum\limits_{j=0}^{n-1}h_j\sum\limits_{i=0}^{n-1}w_i^{j-k}\\ &=\sum\limits_{j=0}^{n-1}h_jn[n|j-k]\\ &=nh_k \text{(只有 $j = k$ 的那一项有值)} \end{align} \]

这个公式与DTF相比，左边多一个 n ，右边的 k 变成了 -k，其余一致。

常数优化：非递归FFT

注意到，第 k 个点和第 k + len / 2 个点 由 第 k 个点和第 k + len/2 共同转移来，并且每次len除2。

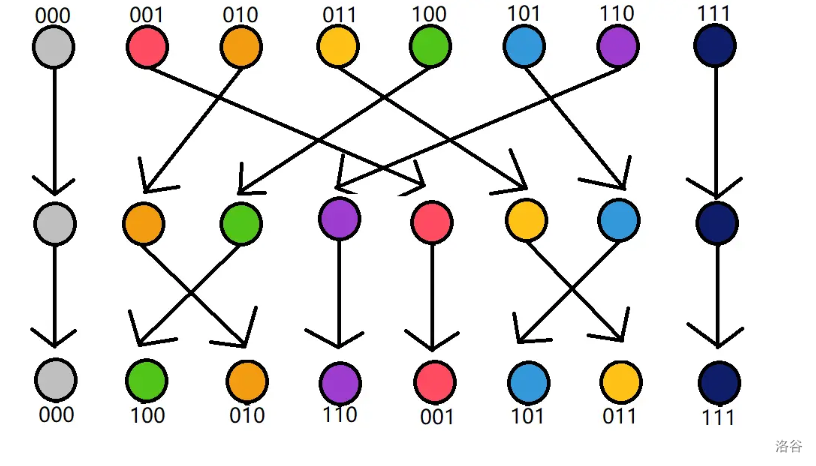
若执行到了第 k 次，那么把从右往左数第 k 位是 0 的数往前提。

所以对于最后一排，最后一位是 0 的排在前面，如果最后一位都是 0，那么倒数第二排是 0 的排在前面...以此类推。

容易发现，这相当于倒着比较二进制数的大小。

考虑最后一行的初始化：第 i 位就应该为 \(f_ {\sim i}\)，$\sim $表示二进制取反。

写成代码是这样的：

  for (int i = 0; i < len; ++i) {rev[i] = rev[i >> 1] >> 1;if (i & 1) rev[i] |= len >> 1;\\变换最高位从左往右第一位？神秘}for (int i = 0; i < len; ++i) if (i < rev[i]) swap(y[i], y[rev[i]]); \\这样才能刚好交换一次

之后就可以从低位向高位递推了。

附上代码：

typedef complex<double > com;
const int N=(1e6+6) * 4;
const double PI = acos(-1);
int n,m,rev[N];
com f[N],g[N];void change(int n) { int L = log2(n);for(int i=0;i<n;++i)rev[i] = (rev[i>>1]>>1) | ((i&1) << (L-1));
}
void FFT(com *f, int n,int op) {change(n)for(int i=0;i<n;++i) if(rev[i] < i) swap(f[i], f[rev[i] ]);for(int mid = 1;mid < n;mid <<= 1){int j = mid << 1; com nxt(cos(PI / mid), sin(PI / mid) * op);for(int st = 0;st < n; st += j){com w(1.0, 0.0);for(int i = st;i < st + (j>>1); ++i, w *= nxt){com tmp1 = f[i],tmp2 = w * f[i + mid];f[i] = tmp1 + tmp2;f[i + mid] = tmp1 - tmp2;}}}
}

参考资料：上课的课件，大佬的博客。