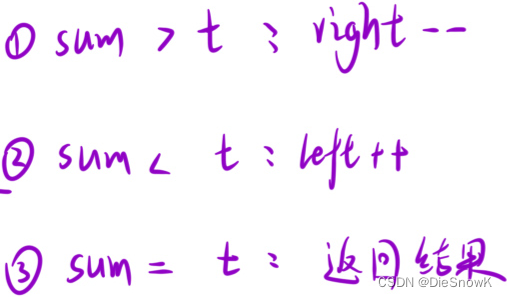目录
- 1.查找总价格为目标值的两个商品
-
- 2.三数之和
-
- 3.四数之和
-
1.查找总价格为目标值的两个商品
1.题目链接
2.算法原理讲解
- 由于本题数据有序,可以利用单调性,用「对撞指针」优化时间复杂度
- 初始化
left,right分别指向数组的左右两端 if (nums[left] + nums[right] == target) if (nums[left] + nums[right] < target) - 对于
nums[left]⽽⾔,此时nums[right]相当于是nums[left]能碰到的最⼤值 - 如果此时不符合要求,说明在这个数组⾥⾯, 没有别的数符合
nums[left]的要求了 - 因此,可以舍去这个数,
left++,去⽐较下⼀组数据
- 那对于
nums[right]⽽⾔,由于此时两数之和是⼩于⽬标值的 nums[right]还可以选择⽐nums[left]⼤的值继续努⼒达到⽬标值- 因此
right指针先不动
if (nums[left] + nums[right] > target) - 同理可以舍去
nums[right],让right--,继续⽐较下⼀ 组数据 - ⽽
left指针不变
3.代码实现
vector<int> TwoSum(vector<int>& price, int target)
{int left = 0, right = price.size() - 1;while (left < right){int sum = price[left] + price[right];if (sum > target){right--;}else if (sum < target){left++;}else{break;}}return { price[left], price[right] };
}
2.三数之和
1.题目链接
2.算法原理讲解
- 思路:
- 排序使数有序,以便简化比较模型,减少比较次数
- 固定一个数
src - 固定一个数之后,剩下两个数就可以用「双指针算法」了
- 在这个数后⾯的区间内,使⽤「双指针算法」快速找到两个数之和等于 − a -a −a即可
- 本题需要去重,有两种思路,本题实现用第二种实现
- 去重:同时要避免越界
- 找到⼀个结果之后,
left和right指针要「跳过重复」的元素 - 当使⽤完⼀次双指针算法之后,固定的
src也要「跳过重复」的元素
- 不漏组合:
- 并非一轮找到一个组合就可以了,可能一轮中可以找到多个组合
- 找到一种结果后,不要停,缩小区间,继续寻找
3.代码实现
vector<vector<int>> ThreeSum(vector<int>& nums)
{sort(nums.begin(), nums.end());vector<vector<int>> ret;int n = nums.size();for(int src = 0; src < n - 2; ){if(nums[src] > 0){break;}int left = src + 1;int right = n - 1;while(left < right){int sum = nums[left] + nums[right];if(sum + nums[src] > 0){right--;}else if(sum + nums[src] < 0){left++;}else{ret.push_back({nums[src], nums[left++], nums[right--]}); while(left < right && nums[left] == nums[left - 1]){left++;}while(left < right && nums[right] == nums[right + 1]){right--;}}}src++;while(src < n && nums[src] == nums[src - 1]){src++;}} return ret;
}
3.四数之和
1.题目链接
2.算法原理讲解
- 基本原理和细节处理与三数之和一模一样
- 只需要在三数之和的基础上多固定一个数就好了
- 也可以理解为:「固定一个数」 + 「三数之和」
- 本题收获->算数转换:
long long sum = (long long)nums[left] + nums[right] + nums[src1] + nums[src2]可能会溢出 - 如果不将等号右边任一数强转为
long long,右边的数之和任然是int类型 - 当算术溢出时,此中间结果由于是int类型,也必然会溢出,无法正常赋值给
long long sum
3.代码实现
vector<vector<int>> FourSum(vector<int>& nums, int target)
{int n = nums.size();vector<vector<int>> ret;sort(nums.begin(), nums.end());int src1 = 0;while(src1 < n -3) {int src2 = src1 + 1;while(src2 < n - 2) {int left = src2 + 1;int right = n - 1;while(left < right){long long sum = (long long)nums[left] + nums[right] + nums[src1] + nums[src2];if(sum > target){right--;}else if(sum < target){left++;}else{ret.push_back({nums[src1], nums[src2], nums[left++], nums[right--]});while(left < right && nums[left] == nums[left - 1]){left++;}while(left < right && nums[right] == nums[right + 1]){right--;}}} src2++;while(src2 < n && nums[src2] == nums[src2 - 1]){src2++;}} src1++;while(src1 < n && nums[src1] == nums[src1 - 1]){src1++;}} return ret;
}