手指计数
我们在数字出现之前,人们怎么计数呢?如何统计人口,统计今天打到了多少猎物?
最开始,人们曾尝试过用手指和脚趾,一指/趾就是 1,双手就是 10,一人就是 20,为此史上有诸多民族曾使用二十进制。藏文中,「人」字有 20 的意思;法语中,80 为 quatre-vingts(4 个 20)。
除了计数,人们也用手指来计算。古代秦晋商人发明了一种数值计算方法,配合口诀,十个手指就是一把算盘,。过去人们为了谋生不会轻易将这种算法的秘笈外传,计算时只见两手在袖中进行,故叫袖里吞金,也叫一掌金。当时还有歌谣曰:
袖里吞金妙如仙,灵指一动数目全。无价之宝学到手,不遇知音不与传。
有关「一掌金」的记述最早见于明代数学家徐心鲁 1573 年《盘珠算法》一书,此书乃我国史上第一部珠算算法专著,只可惜仅在日本内阁文库藏有原本,国内买不到也下载不到。
明代数学家程大位在其《算法统宗》也详细记录了「一掌金」算法 ,靠右手指点左手各指关节完成计算

石子计数
手指计数的缺点:不能存储。例如用 4 个手指表示今天打了 4 个猎物,总不能手一直保持 4 个姿势吧!如何存储呢?
人类最早借助的外物是大自然中随处可见的石子、贝壳、小木棍、玉米粒、豆粒、甚至兽骨。
在英语中,calc 就是小石子的意思,而计算的英文单词,就是 calc 开头的,可见石子与计算有很深的渊源。

到上世纪五十年代为止,我国云南贡山的傈(lì)僳(sù)族 在选举村长时,村民用在候选人面前的碗或竹筒中投放豆子或玉米粒的方式进行投票,最后统计票数(跟我们现在的投票方式本质上是一样的);处理纠纷时,也是以同样的方式,每陈述一条理由就投放一颗玉米粒。
结绳计数
但用石子计数也有缺点:当数量多了,难免会很重,移动起来很困难。聪明的先人想到在绳子上打结。一个绳结可以表示一个数量 1,如果展开来说,根据绳结的大小,位置,花式,材质,颜色等不同,可以表示不同的含义。
结绳不光能用来计数,还有了许多其他用途,结绳记事:
- 《周易郑康成注》一书中有言:「事大,大结其绳;事小,小结其绳。」
- 《贵州苗民概况》一书中提到:「苗人识字甚少,犹保持上古结绳记事遗风。遇事暗中以草记之,简单实例,日久尚能忆之。」
- 在英语中,cord 正是 record 的词根,「记录」源于「绳子」。
结绳通讯:我国普米族将结绳形象地称作「羊毛疙瘩」,即打着一个个结的羊毛绳子。战时,普米族用羊毛疙瘩联络、集合队伍,在一条主绳上系若干细绳,每条细绳代表一个村,一个个的「疙瘩」则表示时间、人物、事件等,此外还附上鸡毛、辣椒、木炭、骨头,分别表示「迅速」、「激烈」、「炽热」、「坚硬」等附加信息。
印加帝国曾设称为 chasqui 的邮差,日行 240 公里,在国内和国际传递「公文」——即结绳。

带着结绳、吹着海螺的 chasqui(图片来自维基「Chasqui」词条)
结绳为约:口说无凭,结绳还常被用做契约,任何时代人们都需要一件契据。《九家易》曰:「古者无文字,其有约誓之事,事大大其绳,事小小其绳,结之多少,随物众寡,各执以相考,亦足以相治也。」
契刻计数
除了结绳,人们还可以用刻痕来计数。远古部落、古代文明,以及近现代的一些少数民族,选用石、木、竹、玉、野兽的牙、角、骨等材料,削成棍、片、圆等形状,也有直接在洞壁上,用坚硬的石器或刀具刻出道道痕迹,用以记录各种数目。我们不妨称之为—— 。

瑞士阿尔卑斯博物馆一瞥——来自阿尔卑斯山脉的契刻(图片来自维基「Tally stick」)词条
契刻的也可用作计数、记事、契约、书信等多种用途。
算筹
你可能没听说过算筹,但「运筹帷幄」、「觥筹交错」这些朗朗上口的成语皆出于此。
算筹本质上只是一根根小小的棍子(长约十几厘米)。棍子的材料多样,竹子、木头、象牙、兽骨、金属、玉器应有尽有。
算筹最早出现于商周,在算盘被发明之前,堪称世界上最先进的计算工具而这所谓先进的计算工具:

像我们随身携带手机一样,懂数学的古人通常会随身佩戴丝布制成的 ,里头放着一把算筹。

传说秦始皇也经常佩带丝质的算袋。一次东游,他把算袋扔进了海里,变化成乌贼,因此乌贼也有算袋鱼之称。明代官员何乔远在万历四十八年(一五二〇年)出版的著作《闽书》中,已整理出自古以来对乌贼的各种名称和传说如下:

到了唐朝,更有法律规定文武百官必须佩带算袋。可见在彼时,算筹不单单是一种计算工具,更是文化和身份的象征。
那么,算筹是如何计算的呢?我们先讲讲算筹是如何表示数的:
算筹用红棍表示正数,黑棍表示负数,有纵横两种「布棍」摆放方法,纵式摆放用竖棍表示 1、横棍表示 5,0 比较特殊,用留空表示。横式摆放指将纵式打横着放:

也就是说,对于不同的数位,纵式、横式是相间使用的,《孙子算经》如是描述:
凡算之法,先识其位。一纵十横,百立千僵,千十相望,万百相当。
举例:个位上的数字用纵式摆放,十位上的用横式摆放,百位上再用纵式摆放,千位再用横式摆放,以此类推。这样奇怪的做法是考虑到 0 的存在,比如 2018:

在实际使用中,空位很容易被忽略,有了纵横交错的做法,即使没有空位,2 和 1 挨在一起,也不会把 2018 当成 218。
那么有了算筹,如何计算呢?例如这是最基本的加法运算:

算筹还能进行很多计算,例如进行乘方和开方,甚至能解线性方程(组)、求最大公约数和最小公倍数、解同余式组、造高阶查分表等等,这里不展开来讲。其所用到的负数、小数、分数等较为抽象的数字概念,比西方早出一百年甚至好几百年。能做如此复杂的计算,得益于古人一代代智慧积累下来的算法口诀,包括沿用至今的九九乘法表。
公元 480 年左右,南北朝数学家祖冲之使用筹算将圆周率精确到小数点后 7 位(3.1415926~3.1415927 之间),这一精度领先世界近千年,直到 15 世纪初才被打破。这一计算涉及包括开方在内的 130 次运算,放到今天,如果不用电子计算设备给你一沓草稿纸,恐怕也很难算准。
算筹的缺点:小木棍的摆放并不方便,但可谓孰能生巧,厉害的筹算者有着相当可观的计算速度,沈括在《梦溪笔谈》中描述:运筹如飞,人眼不能逐。
起初的算筹长约 14 厘米,摆个 6 就要占 200 平方厘米,可以想象,做稍微复杂一点的运算时得放多大一块面积。即使到宋元间改良至寸(3~10cm),面对大计算量的问题依然不好使。宋代马永卿《懒真子》一书就有言:卜者出算子约百余,布地上,几长丈余。
算筹,终被算盘取代。
算盘
算盘的种类有很多,经典的算盘样子如下:

算盘以上珠代表 5,下珠代表 1。按理说,每一个数位从 0~9 只需上一下四,为什么会有上二下五的冗余呢?原因是我国古代十六进制的重量计法,「半斤八两」,1 斤正是 16 两,上二下五正可以用来表示 0~15。
至于算盘的用法,十分简单,将相应数目的算珠推向横梁以表示加上相应数字,推离横梁则表示减去相应数字:

「三下五除二」,一个司空见惯的成语,其实是算盘加法中的一条基本规律:当下档有两颗或多于两颗算珠时,+3 就需要拨下一颗表示 5 的上珠、去除两颗表示 1 的下珠,即 +3 = +5-2。
关于算盘的更多算法,可以参考视频:珠算算法集锦简要,https://www.bilibili.com/video/BV1h741117j5
纳皮尔筹
纳皮尔筹是由纳皮尔发明的算筹,他还发明过对数。纳皮尔筹共有 10 个,序号从 0 到 9,样子如下:

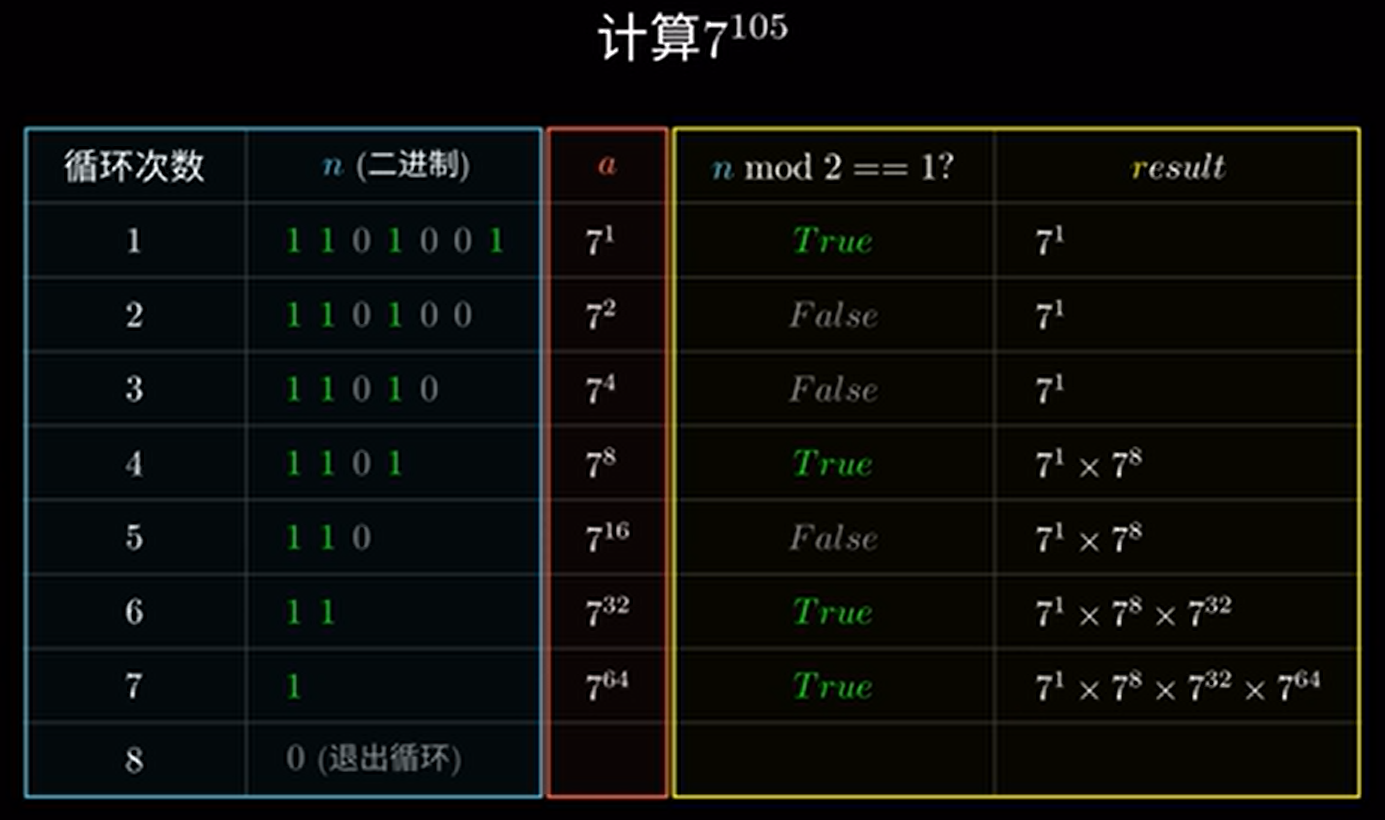
其本质就是一个九九乘法表。例如对于 7 这个算筹,7 × 1 = 1, 7 × 2 = 14 ………… 提前将算好的结果,写在了算筹上。
当我们计算 6785 * 84 的时候:取用被乘数 6、7、8、5 四根筹,而后把目光投到第 8 行上:(因为第 8 行是指 6、7、8、5 每个数字和 8 的乘积)

以斜线为界,对每一位进行相加,超过 9 时通过心算进行进位:

结果一目了然:54280
其本质和我们计算时一样:先得到 8 和每个数字的乘积,然后将他们加起来
6 7 8 5× 8———————————————————————————————————————————————————————————— 4 0 = 8 * 56 4 = 8 * 805 6 = 8 * 7004 8 = 8 * 6000——————————————————————————————————————————————————————————————5 4 2 8 0
这是最简单的乘法,除法的步骤稍微复杂一些,开方运算则更加繁复,还需要引入一种专用的新筹,具体算法在此展开的意义不大,感兴趣的朋友可自行移步维基:https://en.wikipedia.org/wiki/Napier's_bones。
纳皮尔提出对数的概念,引起了计算上的一场革命,极大地促进了天文学、航海学的发展,也为以后物理学的发展奠定了基础。他发明纳皮尔算筹,使用这个计算工具人们可以轻松地计算乘法、除法、平方根以及立方根。纳皮尔算筹广受欢迎,身影遍及整个欧洲。
感兴趣的话可以参考视频:【对数表发明者的计算器:纳皮尔算筹 Napier's Bones】https://www.bilibili.com/video/BV1o54y137ZN
滑尺计算
计算通常是很花时间的,如果能将常用的计算结果存储起来,需要计算的时候,直接去查询,相对能节省很多时间。有了对数后,更是如此。我们讲讲对数的一个基本概念:
loga(M × N) = logaM + logaN
loga(M ÷ N) = logaM - logaN
比如要计算 100 X 1000,查询对数表可知 log100 = 2,log1000 = 3,因此 log100+log1000 = 5,再查逆对数表找到 5 的逆对数 100000,这就是 100 X 1000 的结果。
类似地,除法也可以通过公式 log m/n = log m - log n 转换为减法。幂运算和开方运算也可以使用对数来简化。
更多关于对数的原理,可以参考知乎文章:【延长了天文学家寿命的对数函数】https://zhuanlan.zhihu.com/p/26653057
有了对数,乘除就能化简为加减,大大减轻了当时科学界的计算量。
虽然对数表实现了计算降维,但查阅起来毕竟眼花缭乱,厚厚的书册也不便携带。
不多久,一位叫甘特的英国数学家想到:既然对数表是把两个数的求积问题转换为两个对数的求和,那么,如果把一个对数视为一段可以用直尺丈量的长度,对数之和不就可以利用直尺直接量出来了吗?
1620 年,甘特将对数表刻到一把尺上,借助圆规一类的辅助工具,实现了这种想法。仍以 16×64 为例,先将圆规两脚分别指向和的位置,此时圆规脚的跨度代表着 lg16 的值,而后保持圆规张角不变,平移使其左脚指向乘数 64 的位置,此时右脚所指便是计算结果。

1622 年,另一位英国数学家威廉·奥特雷德觉得圆规有点累赘,不如直接将两把对数尺并排放置,通过相对滑动就可以实现尺上示数的相加,形成了计算尺的雏形:

2 × 3 = 6,对数尺本身可以代替圆规一类的辅助工具(图片来自维基「Slide rule」词条,下同。)
邓稼先、郭永怀、于敏攻克「两弹一星」,离不开计算尺;
黄旭华研制核潜艇,离不开计算尺;
阿波罗登月,飞船上备着计算尺以防不时之需;
冷战期间,美国的冯•布劳恩和前苏联科罗廖夫两位「学科带头人」战功赫赫,用的竟是同一家公司的计算尺……
小结
手动时期是漫长的,几乎从人类出现开始一直贯穿至 17 世纪。
借助外物,人们的计算大大提高,正所谓:假舆马者,非利足也,而致千里;假舟楫者,非能水也,而绝江河。君子生非异也,善假于物也。
但手动时期是蛮荒的,这一时期的工具完全没有自动计算的能力,人们既要动手又要动脑才能得到计算结果。即使有了对数表,也仅仅是预置了答案,并没有计算。
 我们在数字出现之前,人们怎么计数呢?
我们在数字出现之前,人们怎么计数呢?