扫描线
引入
扫描线一般运用在图形上面,它和它的字面意思十分相似,就是一条线在整个图上扫来扫去,它一般被用来解决图形面积、周长,以及二维数点等问题。
面积问题
例题1:【模板】扫描线
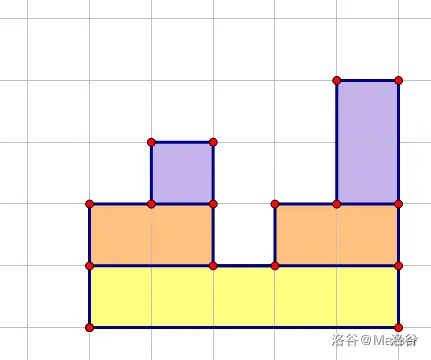
想象有一条线从下往上扫,会将整个图像依次扫描。我们只需要计算出每一条矩形(即图中同一颜色的小矩形)的面积,加起来就是整个图形的面积。
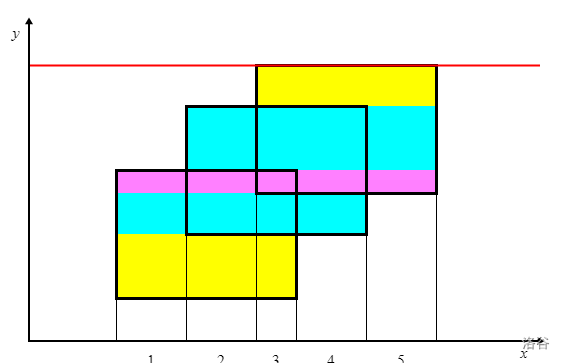
我们将每一条横边存下来并排序。将每个大矩形的下边标记为1,上边标记为-1,这样在扫描中只需要判断标记之和是否大于0即可知道当前扫描线上是否有图形覆盖。
每个大矩形的竖边延长交在x轴上(即图中的虚线),离散化后共有\(tot\)条直线,将有图形覆盖的地方分成\(tot-1\)个部分,我们使用线段树来维护每部分。
从下往上每扫描到一条横边,求出扫描线被图形覆盖的长度(即小矩形的长,\(len\)),乘以该条横边到下一条横边的距离(即小矩形的宽),就是这一条小矩形的面积了。
在\(pushup\)函数中,如果当前节点对应的部分被完全覆盖,那么就可以直接用右竖边坐标减去左竖边坐标算出该部分长度,直接返回,不必继续往下递归。而如果当前节点没有被完全覆盖,那么向下递归求出左右儿子对应部分的长度,加起来作为自己的长度。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
#define ls rt << 1
#define rs rt << 1 | 1
using namespace std;
const int N = 1e6 + 3;
int n;
ll x, y, xx, yy, X[N << 1];
struct ScanLine {ll l, r, h;int flag;bool operator < (const ScanLine& ret) const { return h < ret.h; }
} line[N << 1];
struct SegmentTree {int l, r;int sum; //是否被完全覆盖,不用bool是因为可能在-1前又有其它区间被完全覆盖ll len; //扫描线在当前区间内被覆盖的长度
} t[N << 2];
inline void build(int rt, int l, int r) {t[rt].l = l;t[rt].r = r;if (l == r) return ;rg int mid = (l + r) >> 1;build(ls, l, mid);build(rs, mid + 1, r);
}
inline void pushup(int rt) {if (t[rt].sum) { //被完全覆盖,可以直接相减得出长度 t[rt].len = X[t[rt].r + 1] - X[t[rt].l];} else { //无法通过直接相减得出长度,便将左右子树的长度之和作为自己的长度t[rt].len = t[ls].len + t[rs].len; }
}
inline void add(int rt, ll ql, ll qr, int val) {rg int l = t[rt].l, r = t[rt].r; //该节点管辖的下标范围if (X[r + 1] <= ql || qr <= X[l]) return ;if (ql <= X[l] && X[r + 1] <= qr) { //如果被完全覆盖,直接算 t[rt].sum += val;pushup(rt);return ;}add(ls, ql, qr, val); //否则,先递归再加起来 add(rs, ql, qr, val);pushup(rt);
}
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n;for (rg int i = 1; i <= n; i++) {cin >> x >> y >> xx >> yy;X[(i << 1) - 1] = x;X[i << 1] = xx;line[(i << 1) - 1] = {x, xx, y, 1};line[i << 1] = {x, xx, yy, -1};}n <<= 1;sort(line + 1, line + n + 1);sort(X + 1, X + n + 1);rg int tot = unique(X + 1, X + n + 1) - (X + 1);build(1, 1, tot - 1);rg ll ans = 0;for (rg int i = 1; i < n; i++) { //最后一条边不用管,因为h为0add(1, line[i].l, line[i].r, line[i].flag);ans += t[1].len * (line[i + 1].h - line[i].h); //统计面积}cout << ans << "\n";return qwq;
}
例题2:[poj1151]亚特兰蒂斯
同样是面积的并。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define db double
using namespace std;
const int N = 1e4 + 3;
int n, cnt;
db x, y, xx, yy;
db X[N];
struct ScanLine {db l, r, h;int flag;bool operator < (const ScanLine& ret) { return h < ret.h; }
} line[N << 1];
#define ls rt << 1
#define rs rt << 1 | 1
struct SegmentTree {int l, r;int sum;db len;
} t[N << 2];
inline void build(int rt, int l, int r) {t[rt].l = l;t[rt].r = r;t[rt].sum = 0; //这里记得要清空t[rt].len = 0;if (l == r) return ;rg int mid = (l + r) >> 1;build(ls, l, mid);build(rs, mid + 1, r);
}
inline void pushup(int rt) {if (t[rt].sum) {t[rt].len = X[t[rt].r + 1] - X[t[rt].l];} else {t[rt].len = t[ls].len + t[rs].len;}
}
inline void add(int rt, db ql, db qr, int val) {rg int l = t[rt].l, r = t[rt].r;if (X[r + 1] <= ql || qr <= X[l]) return ;if (ql <= X[l] && X[r + 1] <= qr) {t[rt].sum += val;pushup(rt);return ;}add(ls, ql, qr, val);add(rs, ql, qr, val);pushup(rt);
}
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);while (cin >> n && n) {for (rg int i = 1; i <= n; i++) {cin >> x >> y >> xx >> yy;X[(i << 1) - 1] = x;X[i << 1] = xx;line[(i << 1) - 1] = {x, xx, y, 1};line[i << 1] = {x, xx, yy, -1};}n <<= 1;sort(line + 1, line + n + 1);sort(X + 1, X + n + 1);rg int tot = unique(X + 1, X + n + 1) - (X + 1);build(1, 1, tot - 1);rg db ans = 0;for (rg int i = 1; i < n; i++) {add(1, line[i].l, line[i].r, line[i].flag);ans += t[1].len * (line[i + 1].h - line[i].h);}cout << "Test case #" << ++cnt << "\n";cout << "Total explored area: " << fixed << setprecision(2) << ans << "\n";}return qwq;
}
周长问题
例题3:[IOI1998] [USACO5.5] 矩形周长Picture
将图形周长分为两部分:横边和竖边。
先说竖边:
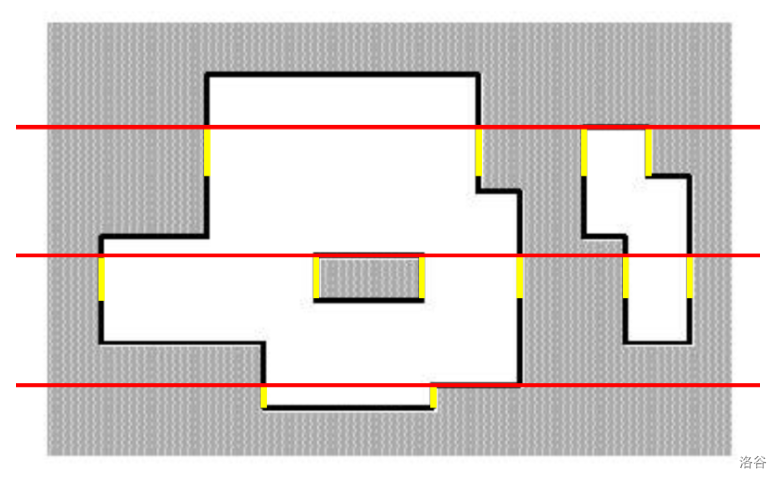
观察扫描线扫过的竖边,总结一下有这样一个结论:竖边总长度\(=\displaystyle\sum2\times\)被当前扫描线截得的整块数\(\times\)扫过的高度。(整块:第一条线上有1个块,第二条线上有3个块,第3条线上有2个块)
注意:如果出现两个高度相同的扫描线,也就是两矩形相邻,那么需要先扫底边再扫顶边,否则会多算。
对于横边:
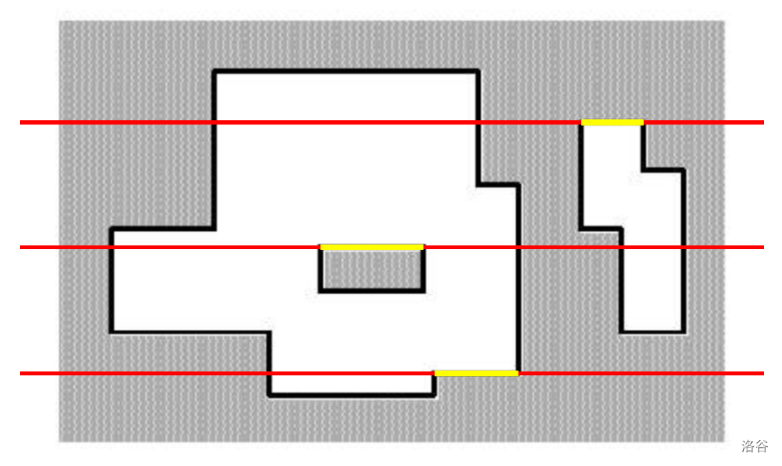
可以得出结论:横边总长度\(=\displaystyle\sum |\)上次截得的总长\(-\)现在截得的总长\(|\)。
所以和面积比起来,周长并中的线段树还要维护线段的条数。另外,横边和竖边需要分别计算。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ls rt << 1
#define rs rt << 1 | 1
using namespace std;
const int N = 1e4 + 3;
int n;
int x, y, xx, yy, pre;
int X[N << 1];
struct ScanLine {int l, r, h, flag;bool operator < (const ScanLine& ret) {if (h == ret.h) return flag > ret.flag; //先扫底边再扫顶边return h < ret.h;}
} line[N << 1];
struct SegmentTree {int l, r;int sum, len;int c; //区间整块数 bool lf, rf; //分别表示左、右端点是否被覆盖
} t[N << 2];
inline void build(int rt, int l, int r) {t[rt].l = l;t[rt].r = r;if (l == r) return ;rg int mid = (l + r) >> 1;build(ls, l, mid);build(rs, mid + 1, r);
}
inline void pushup(int rt) {rg int l = t[rt].l, r = t[rt].r;if (t[rt].sum) {t[rt].len = X[r + 1] - X[l];t[rt].lf = t[rt].rf = true;t[rt].c = 1;} else {t[rt].len = t[ls].len + t[rs].len;t[rt].lf = t[ls].lf; //如果左儿子左端点被覆盖,那么自己的左端点也肯定被覆盖 t[rt].rf = t[rs].rf;t[rt].c = t[ls].c + t[rs].c;if (t[ls].rf && t[rs].lf) t[rt].c -= 1; //如果左儿子右端点和右儿子左端点都被覆盖,那么这是连续的一段,所以要-1}
}
inline void add(int rt, int ql, int qr, int flag) {rg int l = t[rt].l, r = t[rt].r;if (X[l] >= qr || X[r + 1] <= ql) return ;if (ql <= X[l] && X[r + 1] <= qr) {t[rt].sum += flag;pushup(rt);return ;}add(ls, ql, qr, flag);add(rs, ql, qr, flag);pushup(rt);
}
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> n;for (rg int i = 1; i <= n; i++) {cin >> x >> y >> xx >> yy;X[(i << 1) - 1] = x;X[i << 1] = xx;line[(i << 1) - 1] = {x, xx, y, 1};line[i << 1] = {x, xx, yy, -1};}n <<= 1;sort(line + 1, line + n + 1);sort(X + 1, X + n + 1);rg int tot = unique(X + 1, X + n + 1) - (X + 1);build(1, 1, tot - 1);rg int ans = 0;for (rg int i = 1; i < n; i++) {add(1, line[i].l, line[i].r, line[i].flag);ans += abs(pre - t[1].len); //统计横边pre = t[1].len;ans += 2 * t[1].c * (line[i + 1].h - line[i].h); //统计竖边 }ans += line[n].r - line[n].l;cout << ans << "\n";return qwq;
}
二维数点问题
例题4:窗口的星星
设某颗星星的坐标为\((x,y)\),则当窗户的右上角端点的坐标出现在\((x\sim x+w,y\sim y+h)\)这个范围内时,星星就会出现在窗户里。
因为题目中说出现在窗户边框的星星不算,我们不妨将框的长宽都减小0.5,所以坐标边界要-1,即\((x+w-1,y+h-1)\)。但我的写法本就没有竖边上的重合,因此为\((x+w,y+h-1)\)。
于是我们可以将每个星星都扩展成一个矩形,这时我们注意到,若两个矩形之间有交集,它们便可以放在同一个窗户中。
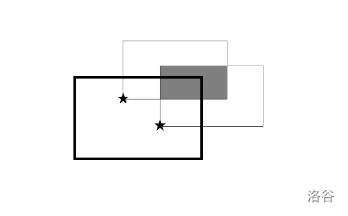
图中灰色部分就是两个星星构成的矩形的交集,只要窗户的右上角端点在灰色区域内,就能同时框住两个星星。
此时我们可以将问题转化为:平面上有若干个矩形,每个矩形都带有一个权值,求在哪个坐标上权值的总和最大。
我们直接将横边的权值设为星星的亮度,此时只需要求出扫描线上的区间最大值即可。
注意:对于上下两横边重合的情况,应先加入新边再删除旧边(同例题3)。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define ll long long
#define ls rt << 1
#define rs rt << 1 | 1
using namespace std;
const int N = 2e4 + 3;
int T, n, W, H;
int x, y, l;
int X[N << 1];
struct ScanLine {int l, r, h;ll val;bool operator < (const ScanLine& ret) const {if (h == ret.h) return val > ret.val;return h < ret.h;}
} line[N << 1];
struct SegmentTree {int l, r;ll lazy;ll maxx;
} t[N << 2];
inline void build(int rt, int l, int r) {t[rt].l = l;t[rt].r = r;t[rt].lazy = t[rt].maxx = 0;if (l == r) return ;rg int mid = (l + r) >> 1;build(ls, l, mid);build(rs, mid + 1, r);
}
inline void pushup(int rt) {t[rt].maxx = max(t[ls].maxx, t[rs].maxx);
}
inline void pushdown(int rt) {t[ls].maxx += t[rt].lazy;t[rs].maxx += t[rt].lazy;t[ls].lazy += t[rt].lazy;t[rs].lazy += t[rt].lazy;t[rt].lazy = 0;
}
inline void add(int rt, int ql, int qr, int val) {rg int l = t[rt].l, r = t[rt].r;if (X[r + 1] <= ql || qr <= X[l]) return ;if (ql <= X[l] && X[r + 1] <= qr) {t[rt].lazy += val;t[rt].maxx += val;return ;}pushdown(rt);add(ls, ql, qr, val);add(rs, ql, qr, val);pushup(rt);
}
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);cin >> T;while (T--) {cin >> n >> W >> H;for (rg int i = 1; i <= n; i++) {cin >> x >> y >> l;X[(i << 1) - 1] = x;X[i << 1] = x + W;line[(i << 1) - 1] = {x, x + W, y, l};line[i << 1] = {x, x + W, y + H - 1, -l};}n <<= 1;sort(line + 1, line + n + 1);sort(X + 1, X + n + 1);rg int tot = unique(X + 1, X + n + 1) - (X + 1);build(1, 1, tot - 1);rg int ans = 0;for (rg int i = 1; i < n; i++) {add(1, line[i].l, line[i].r, line[i].val);ans = max(ans, t[1].maxx);}cout << ans << "\n";}return qwq;
}