link:https://acm.hdu.edu.cn/showproblem.php?pid=7458
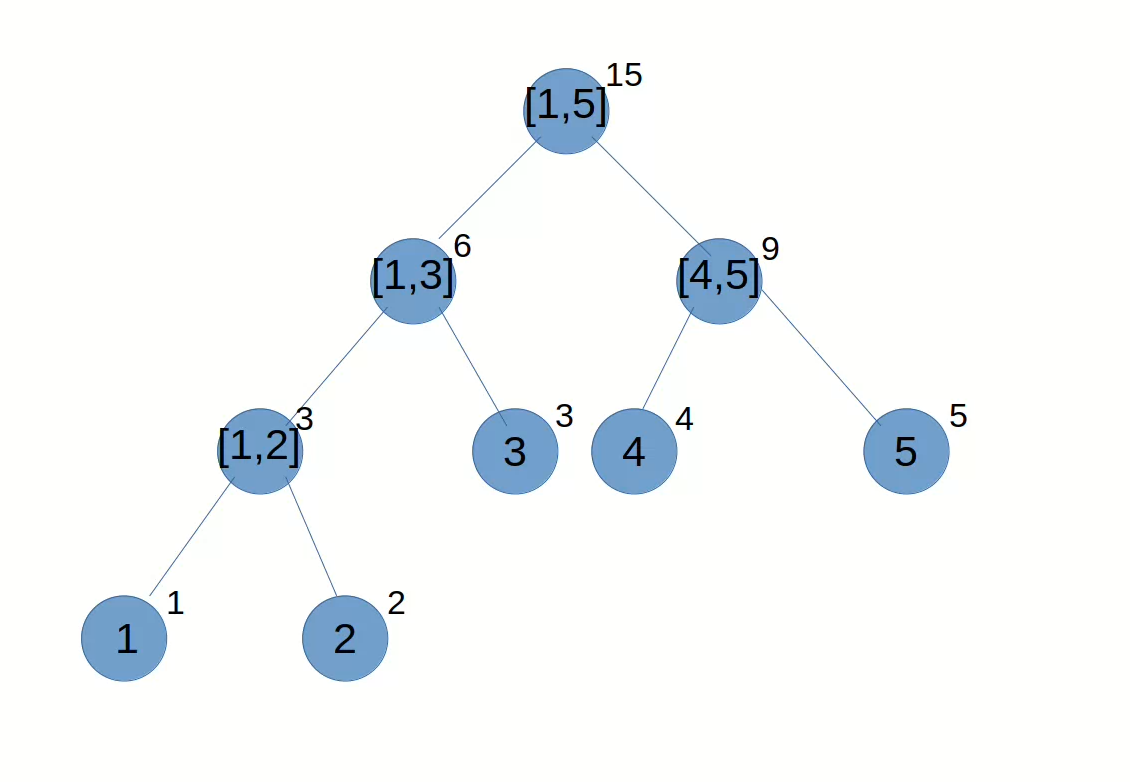
题意:给一棵树,每个点有点权 \(w\) 和颜色 \(c\),选择若干条不相交的路径,每条路径的起始点颜色相同,权值为起始点的权值之和,最大化权值之和。
对每条路径 \((u,v)\) 可以放到LCA上考虑,即我们对每个子树考虑,设 \(f(i,0/1)\) 分别表示在 \(i\) 的子树内,强制选/不选 \(i\) 号点,在子树内能获得的最大收益,\(g(i)=\max(f(i,0),f(i,1))\),记 \(S_u\) 表示 \(u\) 的所有子节点好了,那么:
\[f(x,0)=\sum_{v\in S_x}g(v)
\]
\(f(x,1)\)有几种情情况:从某两个不同的子节点中的某两个同色点连上来的,或者是直接从 \(x\) 作为一个端点连到某个孩子节点的,第一种情况是:

算答案的时候刚好多减去一个 \(g\),所以我们直接对每个子树中每个颜色,维护 \(w_{u1}+\sum (f(u_i,0)-g(u_i))\) 的最大值,因为对每个颜色只关心最大值,可以用一个 map (甚至可以是unordered的)维护,每跳一层就给这个子树做一个全局加 \(f(u,0)-g(u)\) 的操作,用树上启发式合并的办法,同时维护一个加法标记即可。
对于直接从 \(x\) 连下去的情况类似
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define endl '\n'
#define fastio ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
const int N=2e5+5;
int n,c[N];
ll f[N][2],g[N],w[N];
vector<vector<int>> G;int bl[N];
ll tag[N];
map<int,ll> mp[N];
void upd(ll &x,ll y){x=max(x,y);}
void dfs(int x,int fa){f[x][0]=f[x][1]=g[x]=0;for(auto to:G[x])if(to!=fa){dfs(to,x);f[x][0]+=g[to];}for(auto v:G[x])if(v!=fa){if(mp[bl[v]].count(c[x]))upd(f[x][1],(mp[bl[v]][c[x]]+tag[bl[v]])+f[x][0]+w[x]);//merge v to x;if(mp[bl[v]].size()>mp[bl[x]].size())swap(bl[v],bl[x]);//calcfor(auto [col,val]:mp[bl[v]]){if(mp[bl[x]].count(col))upd(f[x][1],(val+tag[bl[v]])+(mp[bl[x]][col]+tag[bl[x]])+f[x][0]);}//mergefor(auto [c,val]:mp[bl[v]]){if(mp[bl[x]].count(c))upd(mp[bl[x]][c],val+tag[bl[v]]-tag[bl[x]]);else mp[bl[x]][c]=val+tag[bl[v]]-tag[bl[x]];}}if(mp[bl[x]].count(c[x]))upd(mp[bl[x]][c[x]],w[x]-tag[bl[x]]);else mp[bl[x]][c[x]]=w[x]-tag[bl[x]];g[x]=max(f[x][0],f[x][1]);tag[bl[x]]+=f[x][0]-g[x];
}void solve(){cin>>n;rep(i,1,n)cin>>c[i];rep(i,1,n)cin>>w[i];G=vector<vector<int>> (n+1);rep(i,1,n)bl[i]=i,tag[i]=0,mp[i].clear();rep(i,1,n-1){int u,v;cin>>u>>v;G[u].push_back(v);G[v].push_back(u);}dfs(1,-1);// rep(i,1,n)cout<<f[i][0]<<' '<<f[i][1]<<' '<<g[i]<<endl;cout<<g[1]<<endl;
}
int main(){fastio;int tc;cin>>tc;while(tc--)solve();return 0;
}