Pinely Round 4 (Div. 1 + Div. 2)-编程知识

Pinely Round 4 (Div. 1 + Div. 2)

news/2024/9/8 19:20:45/文章来源:https://www.cnblogs.com/luckyblock/p/18329250

写在前面
A
B
C
D
E
F
写在最后

写在前面

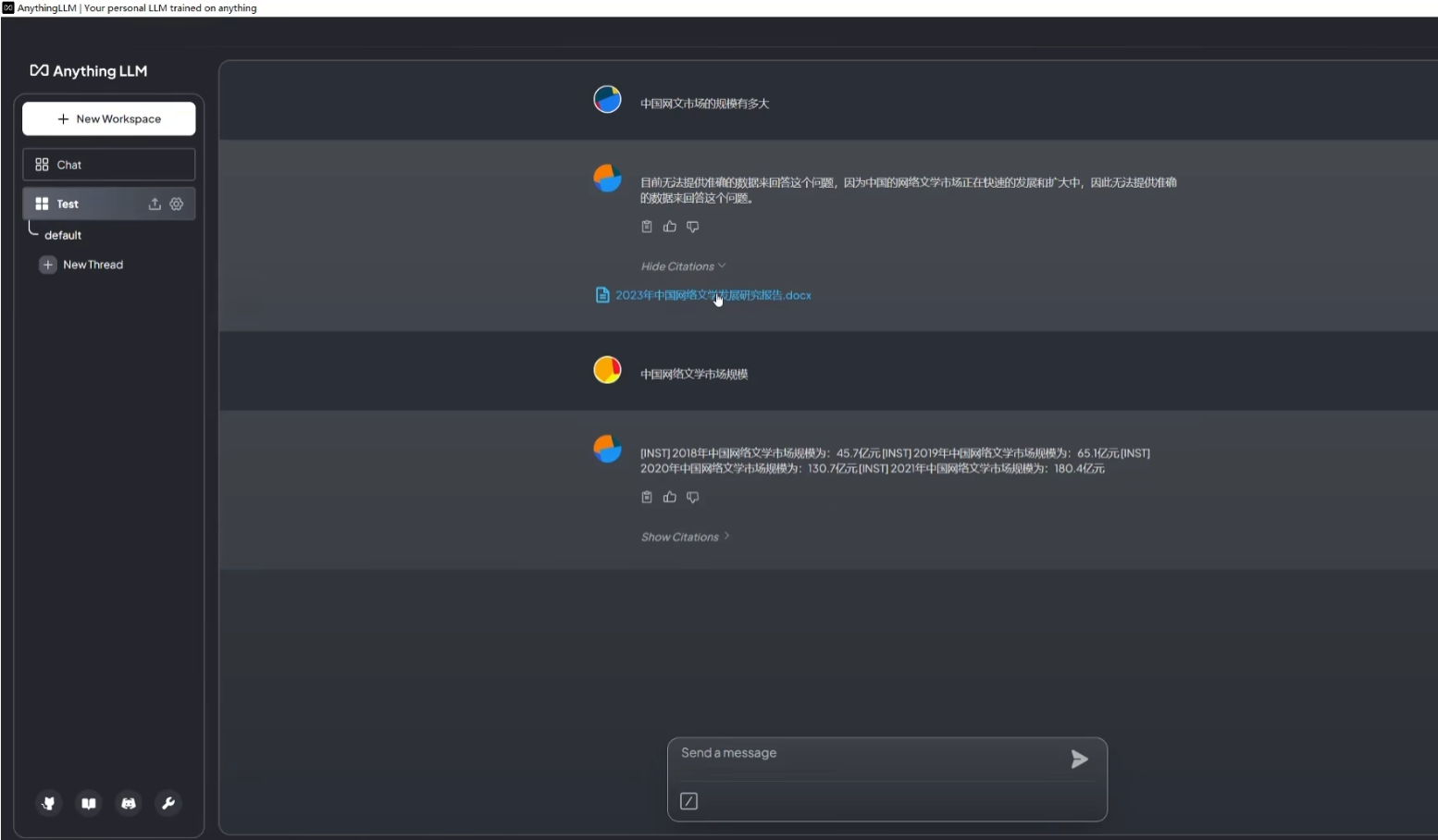
比赛地址：https://codeforces.com/contest/1991

离上紫一步之遥了这场打完又掉下去了哈哈真是太搞

A

签到。

对于每个位置检查两侧数的数量是否为奇数，若为奇数则无法删的只剩这个位置。

//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
//=============================================================
int a[1000];
//=============================================================
//=============================================================
int main() {//freopen("1.txt", "r", stdin);std::ios::sync_with_stdio(0), std::cin.tie(0);int T; std::cin >> T;while (T --) {int n; std::cin >> n;for (int i = 1; i <= n; ++ i) std::cin >> a[i];int ans = 0;for (int i = 1; i <= n; ++ i) {if ((i - 1) % 2 == 1 || (n - i) % 2 == 1) continue;ans = std::max(ans, a[i]);}std::cout << ans << "\n";}return 0;
}

B

构造。

考虑到 AND 运算等价于取两个操作数二进制位的公共 1 部分，一个显然的想法是先构造 \(a_i = b_{i} \operatorname{OR} b_{i + 1}\) 然后如何分别取出其中的公共部分得到 \(b_i\) 和 \(b_{i + 1}\)。上述构造已经可以满足 \(b_2\sim b_{n - 2}\) 的要求，仅需再令 \(a_1 = b_1, a_{n} = b_{n - 1}\)，检查下是否合法即可。

上述构造的原理是下列两式：

\[x\operatorname{AND}y = x\operatorname{OR} y \operatorname{AND} x = x\operatorname{OR} y \operatorname{AND} y \]

\[(x\operatorname{OR} y) \operatorname{AND} (y \operatorname{OR} z)= y \]

//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
//=============================================================
int n, a[100010], b[100010];
//=============================================================
//=============================================================
int main() {// freopen("1.txt", "r", stdin);std::ios::sync_with_stdio(0), std::cin.tie(0);int T; std::cin >> T;while (T --) {std::cin >> n;for (int i = 1; i < n; ++ i) std::cin >> b[i];for (int i = 1; i <= n; ++ i) a[i] = 0;int flag = 1;a[1] = b[1], a[n] = b[n - 1];for (int i = 2; i < n; ++ i) a[i] = b[i - 1] | b[i];for (int i = 1; i < n; ++ i) {if ((a[i] & a[i + 1]) != b[i]) flag = 0;}if (!flag) std::cout << -1 << "\n";else {for (int i = 1; i <= n; ++ i) std::cout << a[i] << " ";std::cout << "\n";}}return 0;
}

C

模拟，构造

赛时手玩了下发现每次找到最大值 \(M\)，并取 \(x=\frac{M}{2}\) 进行操作可保证每次值域缩小一半，一定在四十次内可行，写了发交上去就过了呃呃。

一种更好写的做法是依次取 \(x=2^{30}, 2^{29}, 2^{28}, \cdots, 2^0\)。可以保证每次操作后所有数均不大于这次操作的值，则值域是每次缩小至少一半的，保证最后会缩小到 0。

//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
const int kN = 2e5 + 10;
//=============================================================
int n, a[kN];
//=============================================================
//=============================================================
int main() {// freopen("1.txt", "r", stdin);std::ios::sync_with_stdio(0), std::cin.tie(0);int T; std::cin >> T;while (T --) {std::cin >> n;std::priority_queue<int> q;std::vector<int> ans;for (int i = 1; i <= n; ++ i) std::cin >> a[i];for (int i = 1; i <= n; ++ i) q.push(a[i]);int flag = 0;for (int i = 1; i <= 40; ++ i) {if (q.top() == 0) {flag = 1;break;}int x = ((q.top() + 1) / 2);ans.push_back(x);std::queue<int> temp;while (!q.empty()) temp.push(abs(q.top() - x)), q.pop();while (!temp.empty()) q.push(temp.front()), temp.pop();}if (!flag) {std::cout << -1 << "\n";continue;} std::cout << ans.size() << "\n";for (auto x: ans) std::cout << x << " ";std::cout << "\n";}return 0;
}

D

构造，异或

样例好有病妈的骗我去用 mex 构造糖丸了，给个大点的 \(n\) 答案立刻就出来了呃呃

众所周知有四色定理：平面图相邻点颜色不同染色至多四色。于是猜测至多使用四种颜色就能搞定。

发现若不考虑质数 2，则所有边 \((u, v)\) 的两端点一定一奇一偶，仅需按照奇偶性染色就搞定了欧耶；再考虑上质数 2 的影响，则满足有连边的点 \(u, v\) 一定为下列情况之一：

\(u, v\) 奇偶性不同，即二进制位最后一位不同。
\(u, v\) 奇偶性相同，但 \(u \oplus v = 2\)，即二进制位最后一位相同，倒数第二位不同。

发现仅需将所有点按照二进制位最后两位的取值情况（也即 \(\bmod 4\) 的值）分成四个点集，即可保证仅有四个点集之间有边，点集内部没有边相连，则令着四个点集分别染色 1~4 即可。

另外一个思考的方向是差值为 4 的两个数二进制倒数后两位一定相同，且倒数第三位上肯定是一方为 0 一方为 1，即异或值一定是 4 的倍数，一定不是质数则它们之间一定没有边。

特判下 \(n\le 5\) 的情况，对于 \(n\ge 6\) 按照 \(\bmod 4\) 取值染色即可。

//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
//=============================================================
int n;
//=============================================================
//=============================================================
int main() {// freopen("1.txt", "w", stdout);std::ios::sync_with_stdio(0), std::cin.tie(0);int T; std::cin >> T;while (T --) {std::cin >> n;if (n == 1) {std::cout << "1\n1";} else if (n == 2) {std::cout << "2\n1 2";} else if (n == 3) {std::cout << "2\n1 2 2";} else if (n == 4) {std::cout << "3\n1 2 2 3";} else if (n == 5) {std::cout << "3\n1 2 2 3 3";} else if (n >= 6) {std::cout << 4 << "\n";for (int i = 1; i <= n; ++ i) {std::cout << ((i % 4 == 0) ? 4 : (i % 4)) << " ";}}std::cout << "\n";}return 0;
}
/*
int n = 100;for (int i = 1; i <= n; ++ i) {std::cout << i << ":(";std::vector<int> ans;for (int j = 1; j < i; ++ j) ans.push_back(i ^ j);std::sort(ans.begin(), ans.end());for (auto x: ans) if (x < i) std::cout << x << " ";std::cout << ")\n";}
*/

E

二分图，构造

妈的怎么又是构造做了四道构造了都就没点传统题让我玩玩吗还剩两分钟才发现 Bob 的操作没法那么简单于是寄呃呃呃呃

发现 Alice 需要让相邻两个点染上相同颜色才能获胜，又至多用三种颜色，想到是不是与二分图有关。手玩下容易发现 Alice 能够获胜当且仅当给定图不为二分图，Bob 能获胜当且仅当给定图为二分图。于是先 dfs 黑白染色判定下是否为二分图。

对于 Alice 的获胜策略，非二分图无法黑白染色，于是仅需不断输出 1 2 即可。

对于 Bob 的获胜策略需要动点脑子，不能直接在 dfs 枚举点过程中，仅考虑上一个染色的点，按照每轮次的输入进行染色，可能会被如下数据卡掉：

上述数据会卡掉错误做法，是因为 1 2 两个同色点在与他们相连的不同色点还未被染完之前就被染上了不同的颜色。容易想到染完色之后一定是一种颜色与原图上黑点对应，另外两种颜色与原图上白点对应。考虑到 Alice 给定的两个数中一定含有 1 2 两者中至少一个，于是想到令 1 对应黑点，令 2 对应白点，先仅使用 1 2 进行染色直至原图上黑点白点中一方被染完，在此之后使用 3 和另一方对应数字将剩余的点染色即可。这样即可保证一定可以染完。

由上述必胜策略也可以证明是否为二分图即为 Alice/Bob 获胜的充要条件。

赛后写了 5min 一发过了太搞了哈哈我草

//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
const int kN = 1e4 + 10;
//=============================================================
int n, m, edgenum;
int head[kN], v[kN << 1], ne[kN << 1];
int vis[kN], color[kN];
//=============================================================
void init() {edgenum = 0;for (int i = 1; i <= n; ++ i) head[i] = vis[i] = 0;
}
void addedge(int u_, int v_) {v[++ edgenum] = v_;ne[edgenum] = head[u_];head[u_] = edgenum;
}
bool dfs(int u_, int color_) {vis[u_] = 1, color[u_] = color_;for (int i = head[u_]; i; i = ne[i]) {int v_ = v[i];if (vis[v_]) {if (color[v_] == color_) return false;  } else {if (!dfs(v_, color_ ^ 1)) return false;}}return true;
}
void alice() {std::cout << "Alice\n";std::cout.flush();for (int i = 1; i <= n; ++ i) {std::cout << "1 2\n";std::cout.flush();int x, y; std::cin >> x;if (x == -1) exit(0);std::cin >> y;}
}
void bob() {std::cout << "Bob\n";std::cout.flush();std::vector<int> node[3];for (int i = 1; i <= n; ++ i) {node[color[i] + 1].push_back(i);}for (int i = 1; i <= n; ++ i) {int x, y; std::cin >> x;if (x == -1) exit(0);std::cin >> y;    if (x == 3) std::swap(x, y);if (node[1].empty() || node[2].empty()) {int p = (node[1].empty() ? 2 : 1);if (x == p || y == p) std::cout << node[p].back() << " " << p << "\n";else std::cout << node[p].back() << " " << 3 << "\n";node[p].pop_back();} else {if (x != 3 && y != 3 && node[x].size() > node[y].size()) std::swap(x, y);std::cout << node[x].back() << " " << x << "\n";std::cout.flush();node[x].pop_back();}}
}
//=============================================================
int main() {// freopen("1.txt", "r", stdin);// std::ios::sync_with_stdio(0), std::cin.tie(0);int T; std::cin >> T;while (T --) {std::cin >> n;if (n == -1) exit(0);std::cin >> m;init();for (int i = 1; i <= m; ++ i) {int u_, v_; std::cin >> u_ >> v_;addedge(u_, v_), addedge(v_, u_);}if (dfs(1, 0)) bob();else alice();}return 0;
}