CF1264E
你有一张竞赛图,给你竞赛图中 \(m\) 条边的方向,让你对于没有给定的边确定方向使得整张图的三元环个数最多
\(n \leq 50, m \leq \frac{(n-1)n}{2}\)
-
费用流好题
-
三元环是一个非常难考虑的东西,我们考虑求他的补集:不是三元环的个数最少
-
我们发现不是三元环的情况是存在 \((u,x), (u,y)\) 两条边
-
因此我们可以得到整张图中不是三元环的计算方法:
-
\[\sum_{i=1}^n \binom{out_i}{2} \]
-
其中 \(out_i\) 为 \(i\) 点的出度
-
现在的问题变为:有一个数组 \(out_i\),你可以执行 \(\frac{n(n-1)}{2} - m\) 次操作,形如从选择 \(out_u\) 或 \(out_v\) 进行 \(+1\) 操作,最小化上述式子
-
如果最终要求的式子形如 \(\sum out_i\) 的话固然是一个费用流的板子,但是这并不是
-
我们考虑 \(+1\) 后对答案产生的贡献,我们发现 \(+1\) 后答案增加了 \(out_i\),因此我们有一个连边方案:
-
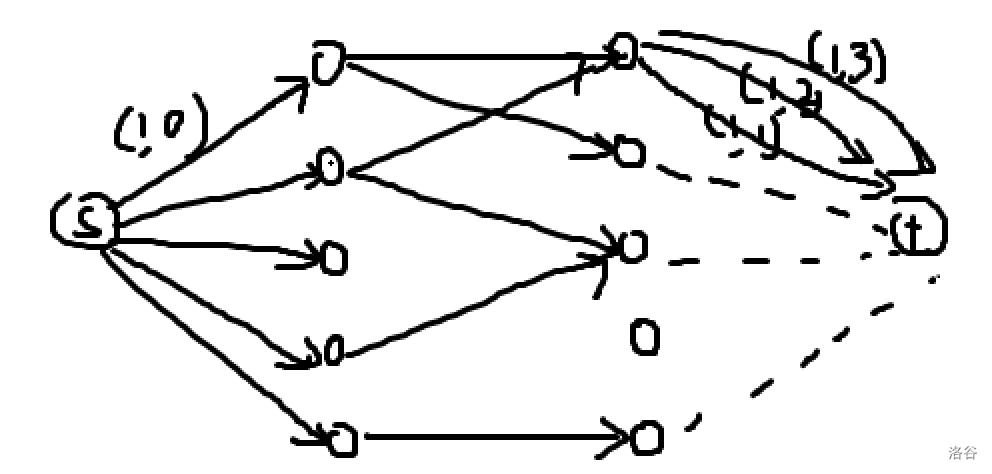
-
如图,我们从超级源点连向 \(\frac{n(n-1)}{2} -m\) 个点流量为 \(1\),费用为 \(0\) 的边表示操作数量,第 \(i\) 个操作对应的点连向 \(u\) 和 \(v\) 一条流量为 \(1\),费用为 \(0\) 的边表示这次操作选择 \(u\) 或 \(v\)
-
而最神奇的操作在于从每一个节点连向超级汇点流量为 \(1\),费用为 \(out_i \sim n\) 的边
-
可以发现,每当某个节点的流量 \(+1\),费用就会增加 \(out_i\)
-
最终复杂度 \(O(n^6m)\),虽然看起来很大,但是这个上界是远远取不到的,可以通过