排列组合:公式及推导
引入
定义:
排列:从指定个数的元素中取出指定个数的元素进行排序;(考虑元素的顺序)
组合:从给定个数的元素中仅仅取出指定个数的元素;(不考虑元素的顺序)
加法&乘法原理
加法原理:
完成一个工程可以有 \(n\) 类办法, \(a_i(i\in[1,n])\) 代表第\(i\) 类方法的数目。则完成这件事共有 \(S=a_1+a_2+a_3+···+a_n\) 种不同的方法。
乘法原理:
完成一个工程需要 \(n\) 个步骤,\(a_i(i\in[1,n])\) 代表第 \(i\) 个步骤的不同方法的数目。那么完成这个工程共有 \(S=a_1 \times a_2 \times a_3 \times ··· \times a_n\) 种不同的方法。
排列与组合基础
排列数:
从 \(n\) 个不同的元素中,任取 \(m(m \leqslant n,m与n均为自然数,下同)\) 个元素按照一定的顺序排成一列,叫做从 \(n\) 个不同元素中 \(m\) 个元素的一个排列;从 \(n\) 个不同元素中取出 \(m(m \le n)\) 个元素的所有排列个数,叫做从 \(n\) 个元素中取出 \(m\) 个元素的排列数,用符号 \(A^m_n\) (或者是 \(P^m_n\) )表示。
排列的计算公式如下:
\(A^m_n =n(n-1)(n-2)..(n-m+1)=\frac{n!}{(n-m)!}\)
\(n!\) 代表 \(n\) 的阶乘,即 \(6!=1 \times 2 \times 3 \times 4 \times 5 \times 6\) 。
公式可以这样理解: \(n\) 个人选 \(m\) 个来排队,队长为 \(n\) ( \(m \leqslant n\) ),第一个位置可以选的人为 \(n\) 个,第二个位置可以选的人为 \(n-1\) 个,以此类推,第 \(m\) 个(最后一个)可以选 \(n-m+1\) 个,得:
全排列: \(n\) 个人来排队,队长为 \(n\) 。第一个位置 可以选 \(n\) 个,第二个位置可以选 \(n-1\) 个,依此类推得:
全排列是排列数的一个特殊情况。
组合数:
从 \(n\) 个不同元素中,任取 \(m(m \leqslant n)\) 个元素组成一个集合,叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的一个组合;从 \(n\) 个不同元素中q取出 \(m(m \leqslant n)\) 个元素组成的所有组合的个数,叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的组合数,用符号 \((^n_m)\) 来表示,读作 $\left\lceil n选m \right\rfloor $ 。
组合数计算公式:
如何理解上述公式?考虑 \(n\) 个人选 \(m\) 个出来 \((m \leqslant n)\) ,不排队,不在乎顺序。如果关心顺序,则为 \(A^m_n\) ,若不关心那么就要除掉重复,那么重复了多少?同样 \(m\) 个人,还要 $\left\lceil 全排列 \right\rfloor $ 得 \(m!\) ,所以得:
组合数也常用 \(\complement^m_n\) 表示,即 \(\complement^m_n=(^n_m)\) 。
组合数也被称为 $\left\lceil 二项式系数 \right\rfloor $ ,下文会阐述其联系。
特别的,当 \(m>n\) 时,\(A^m_n=(^n_m)=0\) 。
插板法
插板法是用于求一类给相同元素分组的方案数的一种技巧,也可用于求一类线性方程组的解的组数。
正整数和的题目
\(Q_1\) :现有 \(n\) 个完全相同的元素,要求将其分为 \(k\) 组,保证每组至少有一个元素,共有多少种分法?
对于这个问题我们可以抽象理解为在 \(n-1\) 个空隙中插入 \(k-1\) 块隔板,将 整个长队分为 \(n\) 部分,两块隔板不能相邻。这样就变成了经典的组合数问题。可得
其本质是求 \(x_1+x_2+x_3+...+x_k=n\) 的正整数解的组数。
非负整数和的题目
\(Q_2\) :若允许为空呢?
此时没法插板了,因为可能会出现很多板子插到一个空的情况,非常不好计算。因此,我们考虑加以约束,使其转化为有限制的 \(Q_1\) 。先借 \(k\) 个元素,平均分配到 \(k\) 组,在 \(n+k\) 个元素形成的 \(n+k-1\) 个空里插板,则
由于元素是完全相同的,在分完组后,从每一组中都拿走一个,对结果是完全没有影响的,也就是结果相等。
其本质是求 \(x_1+x_2+x_3+...+x_k=n(x_i\geqslant 0)\) 的非负整数解的组数。
不同下界整数和的题目
\(Q_3\) :若每组至少有 \(t\) 个元素呢?
此时,对于插板法,会导致版的间隔增大,不好计算。同 \(Q_2\) ,看看如何转化为 \(Q_1\) 。先将 \(t-1\) 个元素压入各组,则转化为在 \(n-k(t-1)-1 (特别的,定义n-1>k(t-1))\) 个空隙中插板。
不相邻的排列
在 \([1,n]\) 中选 \(k\) 个,这 \(k\) 个数中任何两个数都不相邻的组合由有 \(\complement^{k}_{n-k-1}\) 种。
二项式定理
二项式定理阐明了一个展开式的系数:
采用数学归纳法:
手演一遍,会发现对于 \({(a+b)}^n\) 当 \(n=0\) 时,此时等于 \(1\) ,以此类推,分别为
为一时: \({(a+b)^1}=a+b\)
为二时: \({(a+b)}^2=(a+b)(a+b)=a^2+2ab+b^2\)
为三时: \({(a+b)^3}=(a+b){(a+b)}^2=a^3+3a^2b+3ab^3+b^3\)
现在可以找一下规律。
我们将其写作一个塔的样子:
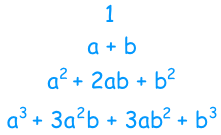
现在只看系数:
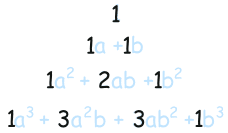
是不是非常熟悉?
是的,这便是杨辉三角:
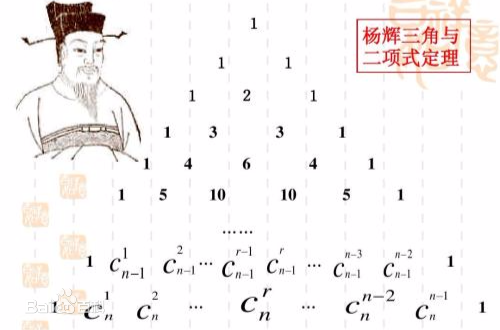
杨辉三角是二项式定理的一种图形上的显式呈现,杨辉三角向我们呈现了组合的一个性质,即:
不仅如此,对于 \((a+b)^n\) 的展开式来说,其中的各项系数依次对应杨辉三角的第 \(n+1\) 行中的每一项 (二项式定理)。
二项式系数
二项式系数可以排列成帕斯卡三角形(杨辉三角形)。若将二项式系数排成一行,在从上向下排列,则构成帕斯卡三角形。
二项式系数常见于各数学领域中,尤其是组合数学。事实上,其可以理解为从 \(n\) 个相异的的元素中选出 \(k\) 个元素的方法数。二项式系数的定义可以推广至 \(n\) 是复数的情况,而且仍被称为二项式系数。