2-梯度下降算法

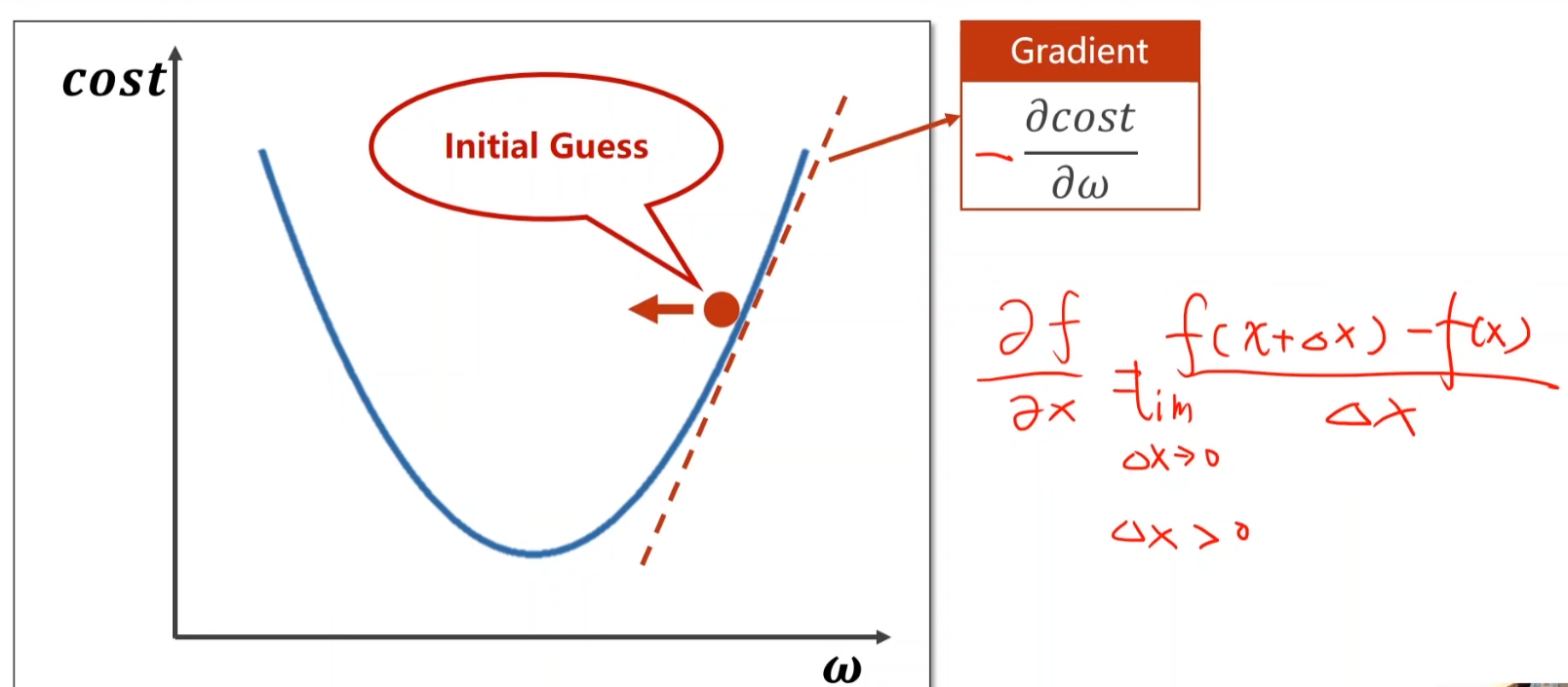
梯度下降算法只能保证找到的是局部最优，不是全局最优

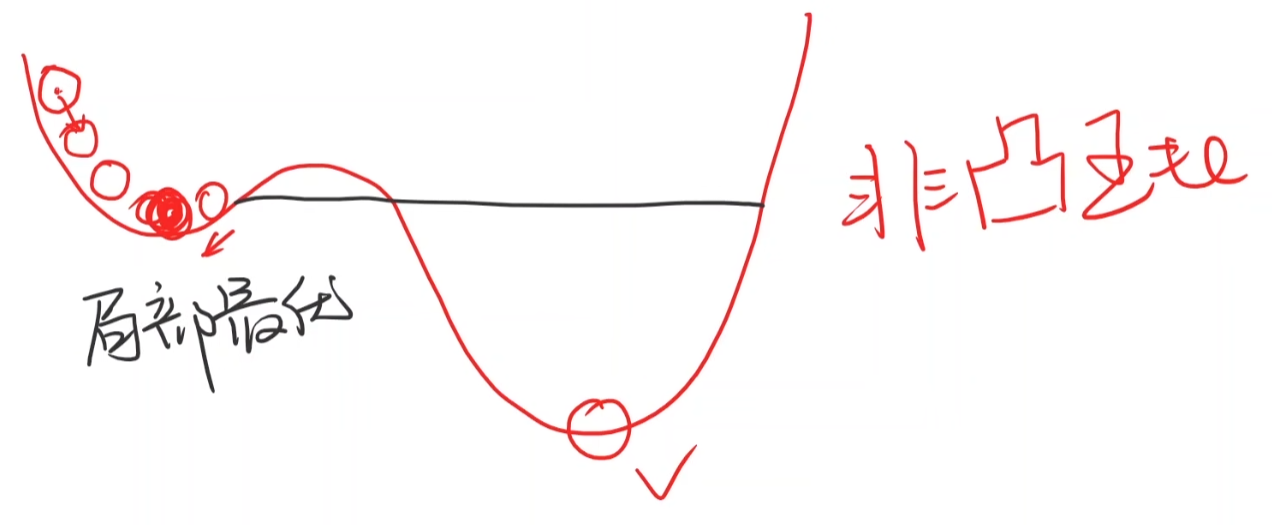
平常我们经过大量实验，发现局部最优点不是很多，所以可以使用梯度下降算法。
但是还要提防鞍点

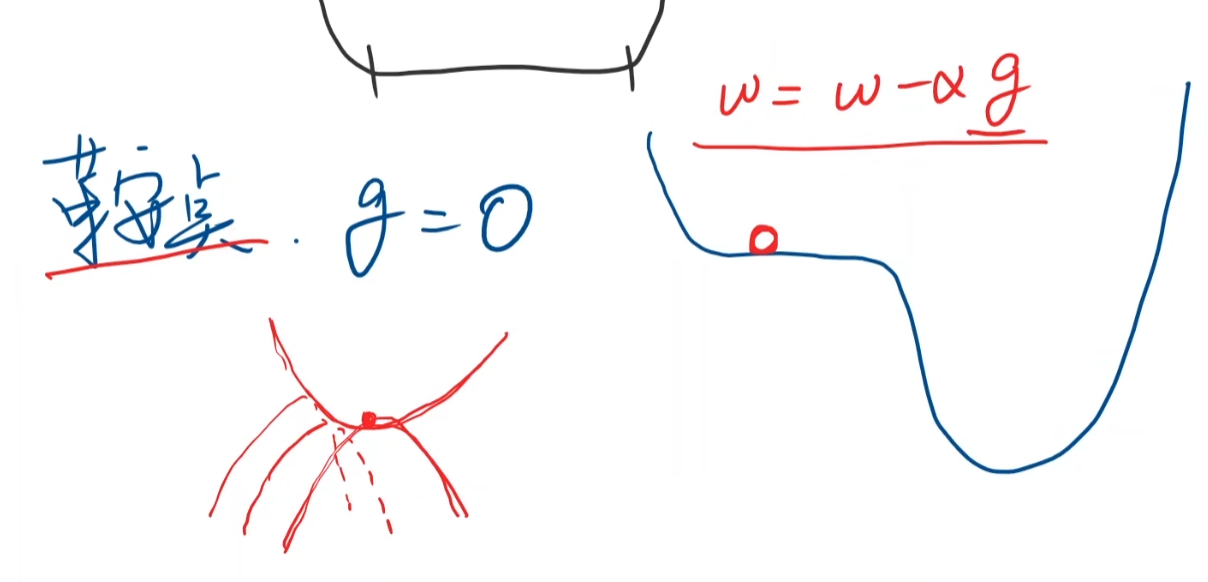
下面进行实现梯度下降算法

点击查看代码

import numpy as np
import matplotlib.pyplot as pltx_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]w = 1.0  # 初始化wdef forward(x):return w * xdef cost(x_data, y_data):cost = 0for x, y in zip(x_data, y_data):y_pred = forward(x)cost += (y_pred - y) ** 2return  cost/len(x_data)def gradient(x_data, y_data):grad = 0for x, y in zip(x_data, y_data):grad += 2 * x * (x * w - y)return grad/len(x_data)epoch_list = []
cost_list = []for epoch in range(100): # 进行100轮训练cost_val = cost(x_data, y_data) # 记录每轮训练的损失值grad_val = gradient(x_data, y_data)w -= 0.01 * grad_val # 梯度下降算法epoch_list.append(epoch)cost_list.append(cost_val)print('Epoch: ', epoch, 'loss: ', cost_val, 'w: ', w)print('After training:', forward(4))plt.plot(epoch_list, cost_list)
plt.show()

有时候cost会不平滑

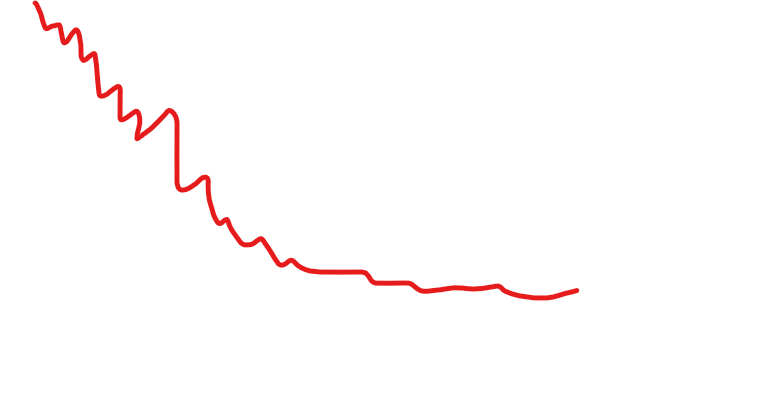
为了绘图的时候更加平滑，可以对cost做指数加权平均