Java数组07：稀疏数组

1. 线性结构

• 线性结构是最常用的数据结构，其特点是数据元素之间存在一对一的线性关系。
• 线性结构有两种不同存储结构，即顺序存储结构和链式存储结构。
• 顺序存储的线性表称为顺序表，顺序表中的存储元素是连续的,即在内存中是连续的，例如数组。
• 链式存储的线性表称为链表，链表中的存储元素不一定是连续的，元素节点中存放数据元素以及相邻元素的地址信息，但好处是可以充分利用碎片地址。
• 线性结构常见的有：数组、队列、链表和栈，后面我们会详细讲解。

---

2. 非线性结构

非线性结构不是一对一的关系， 非线性结构包括：二维数组，多维数组，广义表，树结构，图结构

---

3. 稀疏数组

先看一个需求，在编写五子棋程序时，有存盘退出和续上盘的功能。

因为该二维数组的很多值是默认值 0, 因此记录了很多没有意义的数据，因此，在这里，我们需要引入一个新的概念——稀疏数组

当一个数组中大部分元素为０，或者为同一个值的数组时，可以使用稀疏数组来保存该数组，稀疏数组的处理方法是：

• 记录数组一共有几行几列，有多少个不同的值
• 把具有不同值的元素的行列及值记录在一个小规模的数组中，从而缩小程序的规模

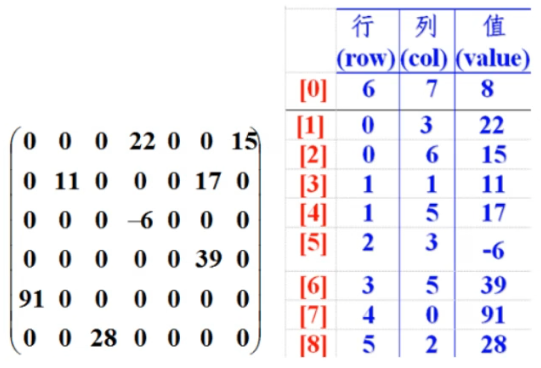
即第一行第一列记录记录原始数组行数，第一行第二列记录原始数组列数，第一行第三列总共有多少个值，第二行记录第一个有效数据，第三行记录第二个有效数据

代码实现

public class SparseArr {public static void main(String[] args) {//创建一个二维数组 11*11//0表示没有棋子，1表示黑棋，2表示蓝棋int[][] chessArr = new int[11][11];chessArr[1][2] = 1;chessArr[2][3] = 2;//输出原始的二维数组System.out.println("原始的二维数组：");for (int i = 0; i < chessArr.length; i++) {for (int j = 0; j < chessArr[i].length; j++) {System.out.print(chessArr[i][j]+"\t");}System.out.println();}//将二维数组转换为稀疏数组//1.先遍历二维数组得到非零数据的个数int sum = 0;for (int i = 0; i < 11; i++) {for (int j = 0; j < 11; j++) {if (chessArr[i][j] != 0){sum++;}}}//2.创建对应的系数数组int[][] sparseArr = new int[sum+1][3];//给系数数组赋值sparseArr[0][0] = 11;sparseArr[0][1] = 11;sparseArr[0][2] = sum;//遍历二维数组将非零的值存放到稀疏数组int count = 0;for (int i = 0; i < chessArr.length; i++) {for (int j = 0; j < chessArr[i].length; j++) {if (chessArr[i][j] != 0){count++;sparseArr[count][0] = i;sparseArr[count][1] = j;sparseArr[count][2] = chessArr[i][j];}}}//输出稀疏数组System.out.println();System.out.println("稀疏数组：");for (int i = 0; i < sparseArr.length; i++) {System.out.println(sparseArr[i][0]+"\t"+sparseArr[i][1]+"\t"+sparseArr[i][2]);}//将稀疏数组恢复成二维数组//1.先读取稀疏数组的第一行，根据第一行创建二维数组int[][] chessArr2 = new int[sparseArr[0][0]][sparseArr[0][1]];//2.读取稀疏数组后几行赋值给二维数组//注意这里是从第二行开始for (int i = 1; i < sparseArr.length; i++) {chessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];}System.out.println();System.out.println("恢复后的二维数组：");for (int[] row : chessArr2) {for (int data : row) {System.out.print(data+"\t");}System.out.println();}}
}

---