非线性规划的经典例题--选址问题

本章会介绍如何利用非线性规划解决选址问题，这个问题是文章线性规划在数学建模中的两道例题中第二道投料问题的第二小题，本章为基于这道题的基础上进行介绍，建议读者返回去看一看

目录

• 一、问题提出
• 二、问题分析
• 三、模型建立
• 四、代码实现
  • 1.输入目标函数
  • 2.输入线性约束

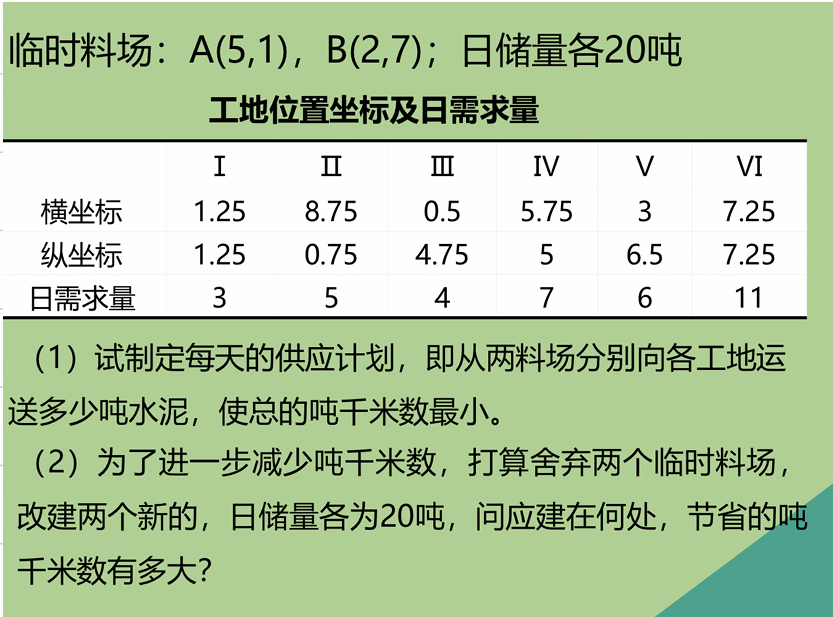
一、问题提出

二、问题分析

第二小问的目标函数其实与第一小问的一样，都是求吨千米数最小。但不同的是，在第一小问的背景下，目标函数仅仅是一个一个ax+bx+....的求和形式，是一个线性规划。
但第二小问把ai与bi的变成了一个目标变量，就成了一个非线性规划

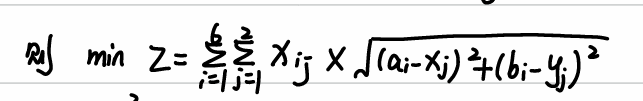
三、模型建立

第二小问的模型在第一小问的基础上添加了4个决策变量，为两个工地的横纵坐标，此外变成了一个非线性规划

四、代码实现

1.输入目标函数

相对第一问直接输入系数向量，输入目标函数更麻烦，这里需要把新料场的坐标当作目标变量给写进函数里。这里也可以用pdist2函数计算两个坐标的距离，但要求都处理成横向量（也就是说pdist2函数也是可以在函数中处理非数值型的参数）

function f = fun5(xx)  % 注意为了避免和下面的x同号，我们把决策变量的向量符号用xx表示（注意xx的长度为16）a=[1.25  8.75  0.5  5.75  3  7.25];  % 工地的横坐标b=[1.25  0.75  4.75	5  6.5  7.25];   % 工地的纵坐标x = [xx(13)  xx(15)];  % 新料场的横坐标y = [xx(14)  xx(16)];  % 新料场的纵坐标c = [];  % 初始化用来保存工地和料场距离的向量 (这个向量就是我们的系数向量）for  j =1:2for i = 1:6c = [c;  sqrt( (a(i)-x(j))^2 + (b(i)-y(j))^2)];  % 每循环一次就在c的末尾插入新的元素endend% 下面我们要求吨千米数，注意c是列向量，我们计算非线性规划时给定的初始值x0是行向量f = xx(1:12) * c;
end

2.输入线性约束

format long g   %可以将Matlab的计算结果显示为一般的长数字格式（默认会保留四位小数，或使用科学计数法）
% 不等式约束
A =zeros(2,16);  % 注意这里要改成16
A(1,1:6) = 1;
A(2,7:12) = 1;
b = [20,20]';
% 等式约束
Aeq = zeros(6,16);  % 注意这里要改成16
for i = 1:6Aeq(i,i) = 1;  Aeq(i,i+6) = 1;
end
beq = [3 5 4 7 6 11]';  % 每个工地的日需求量
% 上下界
lb = zeros(16,1);
% lb = [zeros(12,1); -inf*ones(4,1)];  两个新料场坐标的下界可以设为-inf% 进行求解
% 注意哦，这里我们只尝试了这一个初始值，大家可以试试其他的初始值，有可能能够找到更好的解。
% 未来我会在遗传算法中再来看这个例题。
x0 = [3 5 0 7 0 1 0 0 4 0 6 10 5 1 2 7];  % 用第一问的结果作为初始值
[x,fval] = fmincon(@funpp,x0,A,b,Aeq,beq,lb)  % 注意没有非线性约束，所以这里可以用[]替代，或者干脆不写
reshape(x(1:12),6,2)