一些定理的总结和应用, 仅个人复习使用.
Laurent 展开: \(f(z)=\sum_{l=-\infty}^{\infty}a_l(z-b)^l\).
留数: \(f(z)\) 在某个孤立奇点的去心邻域内 Laurent 展开的 \(-1\) 次方系数, 记为 \(\left.\operatorname{res}f(z)\right|_{z=b}\).
注意 \(f(z)\) 在 \(z=\infty\) 处留数为 \(t=1/z\) 在 \(t=0\) 处 \(1\) 次项系数的相反数, 即 \(\left.\operatorname{res}f(z)\right|_{z=\infty}=\left.-\operatorname{res}\frac{1}{z^2}f(\frac{1}{z})\right|_{z=0}\).
留数定理: \(f(z)\) 在正向闭合路径 \(C\) 内除有限个孤立奇点 \(b_1,\cdots,b_k\) 处处解析, 则 \(\oint_C f(z)\mathrm d z=\left.2\pi i\sum_{k=1}^{n}\operatorname{res} f(z)\right|_{z=b_k}\).
极点: 若 \(f(z)\) 在 \(b\) 的 Laurent 展开的负幂项最高次为 \(-m\) 次, 称 \(b\) 为 \(f(z)\) 的 \(m\) 阶极点.
欲求其留数, 只要令 \(g(z)=(z-b)^mf(z)\). 利用 Taylor 级数 \(\operatorname{res}f(z)|_{z=b}=[(z-b)^{-1}]f(z)=[(z-b)^{m-1}]g(z)=\frac{g^{(m-1)}(b)}{(m-1)!}\).
部分分式分解: 用留数的办法求部分分式分解的系数.
例如 \(f(z)=\frac{1}{(z-1)^2(z-2)(z-3)}=\frac{A}{(z-1)^2}+\frac{B}{z-1}+\frac{C}{z-2}+\frac{D}{z-3}\).
\(A=\left.\operatorname{res}(z-1)f(z)\right|_{z=b}=\left.\frac{1}{(z-2)(z-3)}\right|_{z=1}=\frac{1}{2}\), \(B=\left.\operatorname{res}f(z)\right|_{z=1}=\left.\frac{\mathrm d}{\mathrm dz}\frac{1}{(z-2)(z-3)}\right|_{z=1}=\frac{3}{4}\), \(C=\left.\operatorname{res}f(z)\right|_{z=2}=\left.\frac{1}{(z-1)^2(z-3)}\right|_{z=2}=-1\), \(D=\left.\operatorname{res}f(z)\right|_{z=3}=\left.\frac{1}{(z-1)^2(z-2)}\right|_{z=3}=\frac{1}{4}\).
小圆弧引理: \(f(z)\) 在 \(z=b\) 空心领域上连续, \(\theta_1\le \arg(z-b)\le \theta_2\), 当 \(|z-b|\to 0\) 时 \((z-b)f(z)\) 一致趋于 \(k\). \(C_\delta\) 是以 \(b\) 为圆心 \(\delta\) 为半径, \(\theta_1\le \arg(z-b)\le \theta_2\) 构成的弧, 则 \(\lim_{\delta\to 0}\int_{C_\delta}f(z)\mathrm d z=ik(\theta_1-\theta_2)\).
大圆弧引理: \(f(z)\) 在 \(\infty\) 点邻域内连续, \(\theta_1\le \arg z\le \theta_2\), 当 \(|z|\to \infty\) 时 \(zf(z)\) 一致趋于 \(K\). \(C_R\) 是以 \(O\) 为圆心 \(R\) 为半径, \(\theta_1\le \arg z\le \theta_2\) 构成的弧. 则 \(\lim_{R\to \infty}\int_{C_R}f(z)\mathrm d z=iK(\theta_2-\theta_1)\).
Jordan 引理: \(0\le \arg z \le \pi\), \(|z|\to \infty\) 时 \(Q(z)\to 0, p>0\), \(C_R\) 是以 \(O\) 为圆心 \(R\) 为半径的上半圆弧. 则 \(\lim_{R\to \infty}\int_{C_R}Q(z)e^{ipz}\mathrm d z=0\).
证明: 设 \(z=Re^{i\theta}\), \(\forall \epsilon>0,\exist M,\forall R>M,|Q(z)|<\epsilon\). 看作对 \(\theta\) 积分, 直接使用三角不等式估计其模长后扔掉形如 \(e^{ic}\) 的结构, 可放缩为 \(2\epsilon R\int_{0}^{\frac{\pi}{2}}e^{-pR\sin \theta}\mathrm d \theta\le 2\epsilon R\int_{0}^{\frac{\pi}{2}}e^{-pR\frac{2\theta}{\pi}}\mathrm d \theta=\frac{\epsilon \pi}{p}(1-e^{-Rp})<\frac{\epsilon \pi}{p}\).
补充引理: \(Q(z)\) 只有有限个奇点, 下半平面中 \(|z|\to \infty\) 时 \(Q(z)\to 0\), \(p>0\), \(C_R\) 是以 \(O\) 为圆心 \(R\) 为半径的上半圆弧. 则 \(\lim_{R\to \infty}\int_{C_R}Q(z)e^{-ipz}\mathrm d z=2\pi i\sum_{\text{全平面}}\operatorname{res}\{Q(z)e^{-ipz}\}=\left.-2\pi i\operatorname{res}\{Q(z)e^{-ipz}\}\right|_{z=\infty}\).
证明考虑下半圆弧对应的积分由 Jordan 引理为 \(0\), 再结合留数定理即证.
例题: 求积分 (1) \(\int_{-\infty}^{\infty}\frac{\mathrm dx}{x(1+x+x^2)}\). (2) \(\int_{-\infty}^{\infty}\frac{\cos x}{x}\mathrm d x\). (3) \(\int_{-\infty}^{\infty}\frac{\sin x}{x}\mathrm d x\).
解: (1) 用小圆弧绕过实数轴上的奇点. 构造如下围道
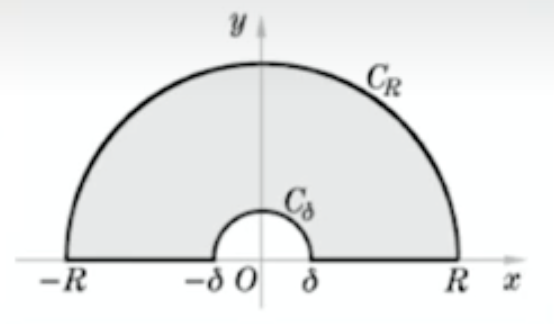
令 \(\omega=e^{\frac{2\pi i}{3}}\), \(f(z)=\frac{1}{z(1+z+z^2)}=\frac{1}{z(z-\omega)(z-\omega^2)}\) 在 \(C\) 内仅有奇点 \(\omega\).
由留数定理, \(\int_{-R}^{-\delta} f(x)\mathrm dx+\int_{\delta}^{R} f(x)\mathrm dx+\int_{C_\delta}f(z)\mathrm dz+\int_{C_R}f(z)\mathrm dz=\oint_C f(z)\mathrm dz=\left.2\pi i\operatorname{res}f(z)\right|_{z=\omega}=\left.2\pi i\frac{1}{z(z-\omega^2)}\right|_{z=\omega}=\frac{2\pi i(\omega-1)}{3}\).
\(\lim_{z\to 0}zf(z)=1\), 由小圆弧引理, \(\lim_{\delta\to 0}\int_{C_\delta}f(z)\mathrm d z=i(0-\pi)=-i\pi\).
\(\lim_{z\to \infty}zf(z)=0\), 由大圆弧引理, \(\lim_{R\to \infty}\int_{C_R}f(z)\mathrm d z=0\).
取极限 \(\delta \to 0,R\to \infty\), 则 \(\int_{-\infty}^{\infty}f(x)\mathrm d x=\int_{-R}^{-\delta} f(x)\mathrm dx+\int_{\delta}^{R} f(x)\mathrm dx=\frac{2\pi i(\omega-1)}{3}+i\pi=-\frac{\pi}{\sqrt{3}}\).
(2), (3) 一起计算, 取 \(f(x)=\frac{e^{i x}}{x}\). 考虑积分 \(\int_{-\infty}^{\infty}f(x)\mathrm d x\). 其实部和虚部分别为 (2) 和 (3) 的答案.
仍然利用 (1) 中的围道, 而 \(f(z)\) 在 \(C\) 内无奇点.
由留数定理, \(\int_{-R}^{-\delta} f(x)\mathrm dx+\int_{\delta}^{R} f(x)\mathrm dx+\int_{C_\delta}f(z)\mathrm dz+\int_{C_R}f(z)\mathrm dz=\oint_C f(z)\mathrm dz=0\).
\(\lim_{z\to 0}zf(z)=1\), 由小圆弧引理, \(\lim_{\delta\to 0}\int_{C_\delta}f(z)\mathrm d z=i(0-\pi)=-i\pi\).
\(|z|\to \infty\) 时, \(\frac{1}{z}\to 0\), 由 Jordan 引理, \(\lim_{R\to \infty}\int_{C_R}\frac{1}{z}e^{iz}\mathrm d z=0\).
取极限 \(\delta\to 0,R\to \infty\), 则 \(\int_{-\infty}^{\infty}f(x)\mathrm d x=\int_{-R}^{-\delta} f(x)\mathrm dx+\int_{\delta}^{R} f(x)\mathrm dx=i\pi\). 故 \(\int_{-\infty}^{\infty}\frac{\cos x}{x}=0, \int_{-\infty}^{\infty}\frac{\sin x}{x}=\pi\).
多值函数积分:
(1) 含幂函数的积分: \(I=\int_{0}^{\infty}x^{s-1}Q(x)\mathrm dx\), 其中 \(s\) 是实数, \(Q(z)\) 单值, 在正实轴上无奇点, 要求 \(\lim_{x\to 0}x^sQ(x)=\lim_{x\to \infty}x^sQ(x)=0\).
考虑相应的复变积分 \(\oint_C z^{s-1}Q(z)\mathrm d z\). 构造如下围道, 规定割线上岸 \(\arg z=0\), 则下岸 \(\arg z=2\pi\).
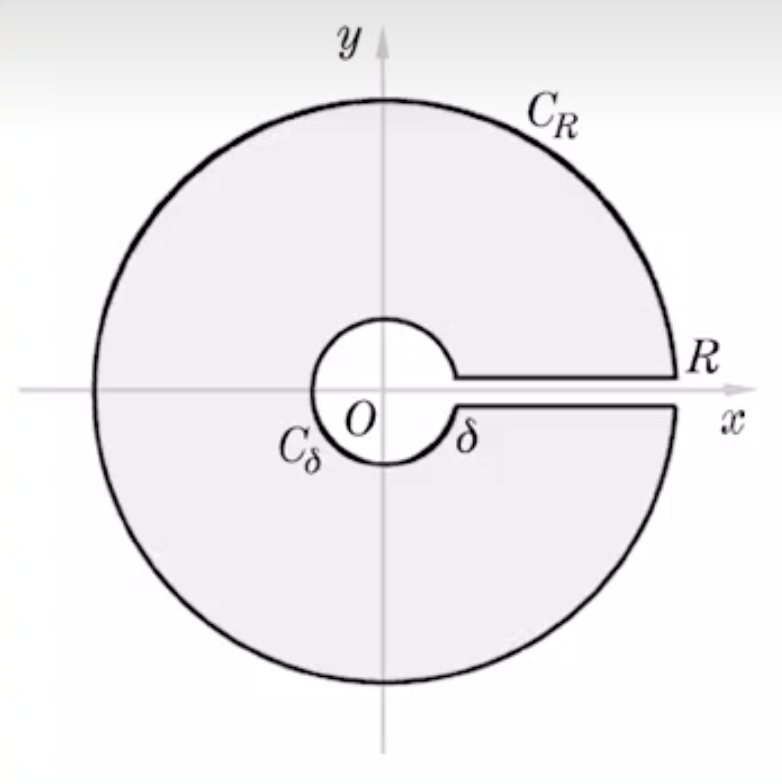
\(2\pi i\sum_{\text{全平面}}\operatorname{res}\{z^{s-1}Q(z)\}=\oint_Cz^{s-1}Q(z)\mathrm d z=\int_{\delta}^{R}x^{s-1}Q(x)\mathrm d x+\int_{C_R}z^{s-1}Q(z)\mathrm d z+\int_{R}^{\delta}(xe^{2\pi i})^{s-1}Q(x)\mathrm d x+\int_{C_\delta}z^{s-1}Q(z)\mathrm d z.\)
由大圆弧引理和小圆弧引理可知 \(\lim_{\delta\to 0}\int_{C_\delta}f(z)\mathrm d z=\lim_{R\to \infty}\int_{C_R}f(z)\mathrm d z=0\).
取极限 \(\delta\to 0,R\to \infty\), 得到 \(I=\frac{2\pi i}{1-e^{2\pi i s}}\sum_{\text{全平面}}\operatorname{res}\{z^{s-1}Q(z)\}\). (注意在计算留数时要保证 \(0\le \arg z\le 2\pi\))
例: \(I=\int_0^{\infty}\frac{x^{\alpha-1}}{1+x}\mathrm dx,0<\alpha<1\). 此时奇点应该理解为 \(z=e^{i\pi}\), 留数为 \(e^{i\pi(\alpha-1)}\), 故 \(I=\frac{2\pi i}{1-e^{2\pi i \alpha}}e^{i\pi(\alpha-1)}=\frac{2\pi i}{e^{\pi i\alpha}-e^{-\pi i\alpha}}=\frac{\pi}{\sin(\pi \alpha)}\).
(2) 含对数函数的积分: \(I=\int_{0}^{\infty}Q(x)\ln x\mathrm d x\). \(Q(z)\) 单值, 在正实轴上没有奇点, 要求 \(\lim_{x\to 0}xQ(x)\ln x=\lim_{x\to \infty}xQ(x)\ln x=0\).
此时应考虑复变积分 \(\oint_C Q(z)\ln^2 z\mathrm d z\), 围道和 (1) 相同. 下岸的 \((\ln x+2\pi i)^2\) 在展开后平方项和上岸抵消, 留下一次项和常数项, 若 \(\lim_{z\to 0}zQ(z)\ln^2 z=\lim_{z\to \infty}zQ(z)\ln^2 z=0\), 根据大圆弧引理和小圆弧引理, 取极限 \(\delta\to 0,R\to \infty\), 最终可以得到 \(-4\pi i\int_{0}^{\infty}Q(x)\ln x\mathrm d x+4\pi^2\int_{0}^{\infty}Q(x)\mathrm d x=2\pi i\sum_{\text{全平面}}\operatorname{res}\{Q(z)\ln^2z\}\), 比较实部和虚部即可.
例: \(\int_{0}^{\infty}\frac{\ln x}{1+x+x^2}\mathrm d x\).
\(\Gamma\) 函数和 \(\Beta\) 函数:
\(\Gamma(z)=\int_{0}^{\infty}e^{-t}t^{z-1}\mathrm d t\), 定义域为 \(\Re(z)>0\).
\(\Beta(p,q)=\int_{0}^{1}t^{p-1}(1-t)^{q-1}\mathrm dt\), 定义域为 \(\Re(p),\Re(q)>0\), 三角换元 \(t=\sin^2\theta\), 则 \(\Beta(p,q)=2\int_{0}^{\frac{\pi}{2}}\sin^{2p-1}\theta\cos^{2q-1}\theta \mathrm d \theta\).
(1) 对 \(\Gamma\) 分布积分可得当 \(z\in \N_{+}\) 时 \(\Gamma(z)=(z-1)!\).
(2) \(\Beta(p,q)=\frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)}\).
证: 将 \(\Gamma(p)=2\int_{0}^{\infty}e^{-x^2}x^{2p-1}\mathrm dx\) 带入得 \(\Gamma(p)\Gamma(q)=4\int_{0}^{\infty}\int_{0}^{\infty}e^{-(x^2+y^2)}x^{2p-1}y^{2q-1}\mathrm d x\mathrm d y =4\int_{0}^{\frac{\pi}{2}}\int_{0}^{\infty}e^{-r^2}(r\cos\theta)^{2p-1}(r\sin \theta)^{2q-1}r\mathrm d r\mathrm d \theta =\Gamma(p+q)\Beta(p,q).\)
(3) 余元公式: \(\Gamma(z)\Gamma(1-z)=\frac{\pi}{\sin(\pi z)}\).
(4) 倍乘公式: \(\Gamma(2z)=2^{2z-1}\pi^{-1/2}\Gamma(z)\Gamma(z+1/2)\).
证明: \(\Gamma(z)\Gamma(1-z)=\Beta(z,1-z)=\int_0^1t^{z-1}(1-t)^{-z}\mathrm d t\xlongequal{x=\frac{t}{1-t}}\int_{0}^{\infty}\frac{x^{z-1}}{x+1}\), 在多值函数积分中我们计算过这就是 \(\frac{\pi}{\sin(\pi z)}\).
参考:《数学物理方法》吴崇试 高春媛.