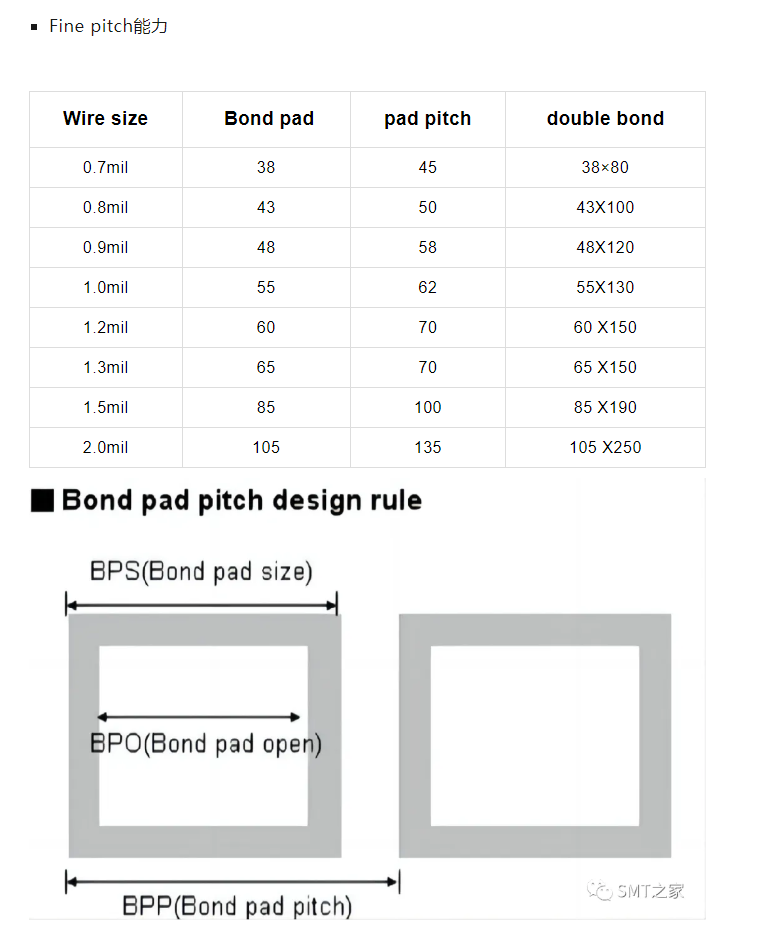
性质
1.
百度百科给的

最主要的性质就是归零和结合,其他的就都是拓展了。
例题:P1469
2.
\(a \bigoplus b<=a+b\)
关于这个不等式比较好的理解为异或就是不进位的加法
例题:luoguP5514
应用
异或哈希
异或跟hash一样,也是会发生冲突的
例如:$1 \bigoplus 2 = 5 \bigoplus 6 $
那我们要怎么去避免冲突呢,我们就可以借助hash的思想,对异或值做一个映射,或基于一个base来达成。
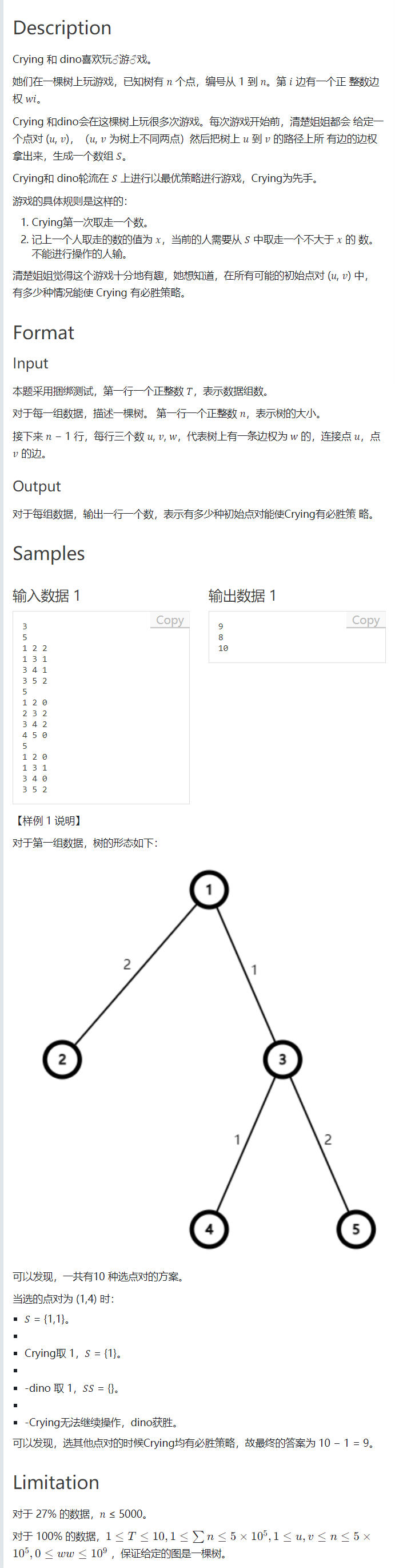
来看这道题,我们先来分析Crying的必胜策略:
假设Crying首先拿最小的数,如果最小的数有奇数个,那Crying会赢,如果为偶数个,那Crying肯定不会上来就拿最小的数,而是先去考虑拿第二小的数,那同样如果第二小的数为奇数个,Crying胜,如果为偶数个,那就接着考虑第三小的数,以此类推……
那转化一下题意就是求保证路径上每个数字不会出现偶数次的路径,再转化一下那这就是要保证路径的异或和不为 \(0\) (异或的归零性质,相同的数两两相抵消)。
但是,这样就会出现一个问题:异或冲突
我们就可以用上面的方法来避免这个问题,那这题就好办了,我们加边的时候给边权乘一个base,然后dfs跑一遍每个点到根节点的异或和,最后统计一下。这个时间限制不支持\(O(n^2)\)的操作,我们就可以开个map存一下dis相同的个数,最后减去即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;#define int long long
const int N=5e6+107;
int n;int read()
{int f=1,s=0;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){s=(s<<1)+(s<<3)+(ch^48);ch=getchar();}return f*s;
}unsigned long long qpow(unsigned long long a,int b)
{unsigned long long ans=1;while(b){if(b&1) ans=ans*a;a=a*a;b=b>>1;}return ans;
}int h[N],to[N],nxt[N],w[N],tot;
void add(int x,int y,int dt)
{to[++tot]=y;nxt[tot]=h[x];w[tot]=dt;h[x]=tot;
}
unordered_map<int,int>mp,vis;int dis[N];
void dfs(int u,int fa)
{for(int i=h[u];i;i=nxt[i]){int v=to[i];if(v==fa) continue;dis[v]=dis[u]^w[i];dfs(v,u);}mp[dis[u]]++;
}void clear()
{memset(h,0,sizeof h);mp.clear(); vis.clear();tot=0;
}signed main()
{int T=read();while(T--){clear();n=read();for(int i=1;i<=n-1;i++){int x=read(),y=read(),dt=qpow(237,read()+1);add(x,y,dt); add(y,x,dt);}dfs(1,0);int ans=n*(n-1)/2;for(int i=1;i<=n;i++){if(vis[dis[i]]) continue;ans-=mp[dis[i]]*(mp[dis[i]]-1)/2;vis[dis[i]]=1;}printf("%lld\n",ans);}
}