问题描述
使用 Lettuce 客户端,在AKS环境中连接Azure Redis服务,出现超时错误。
错误消息:
Redis command timed out , command timed out after 1 minute(s).
错误截图:
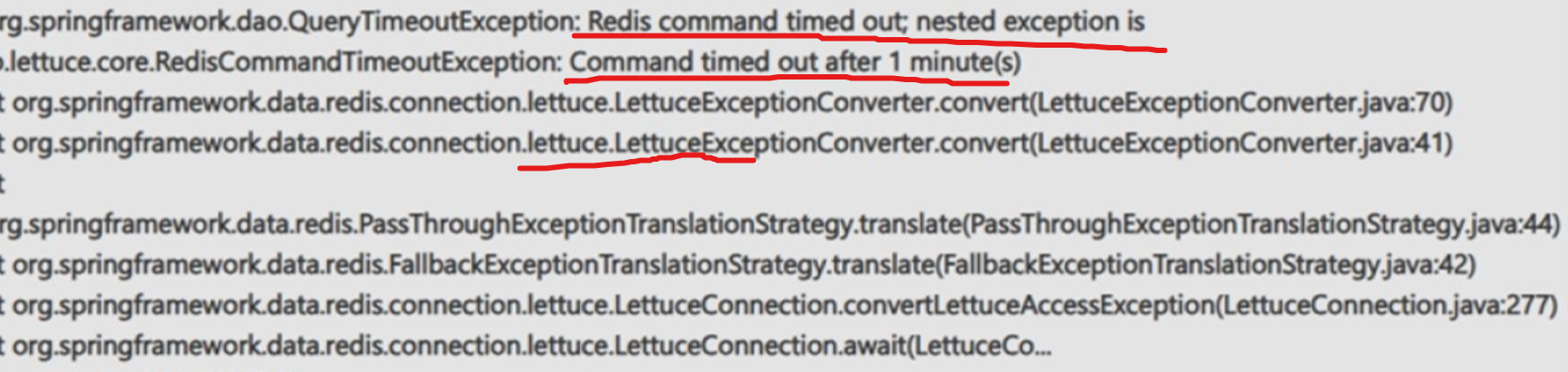
解决思路
当出现Redis客户端连接不上时,需要先排查Redis服务器的状态,比如Server Load是否处于高位(90%以上),CPU是否处于高位,然后查看连接数的情况(Connections)。
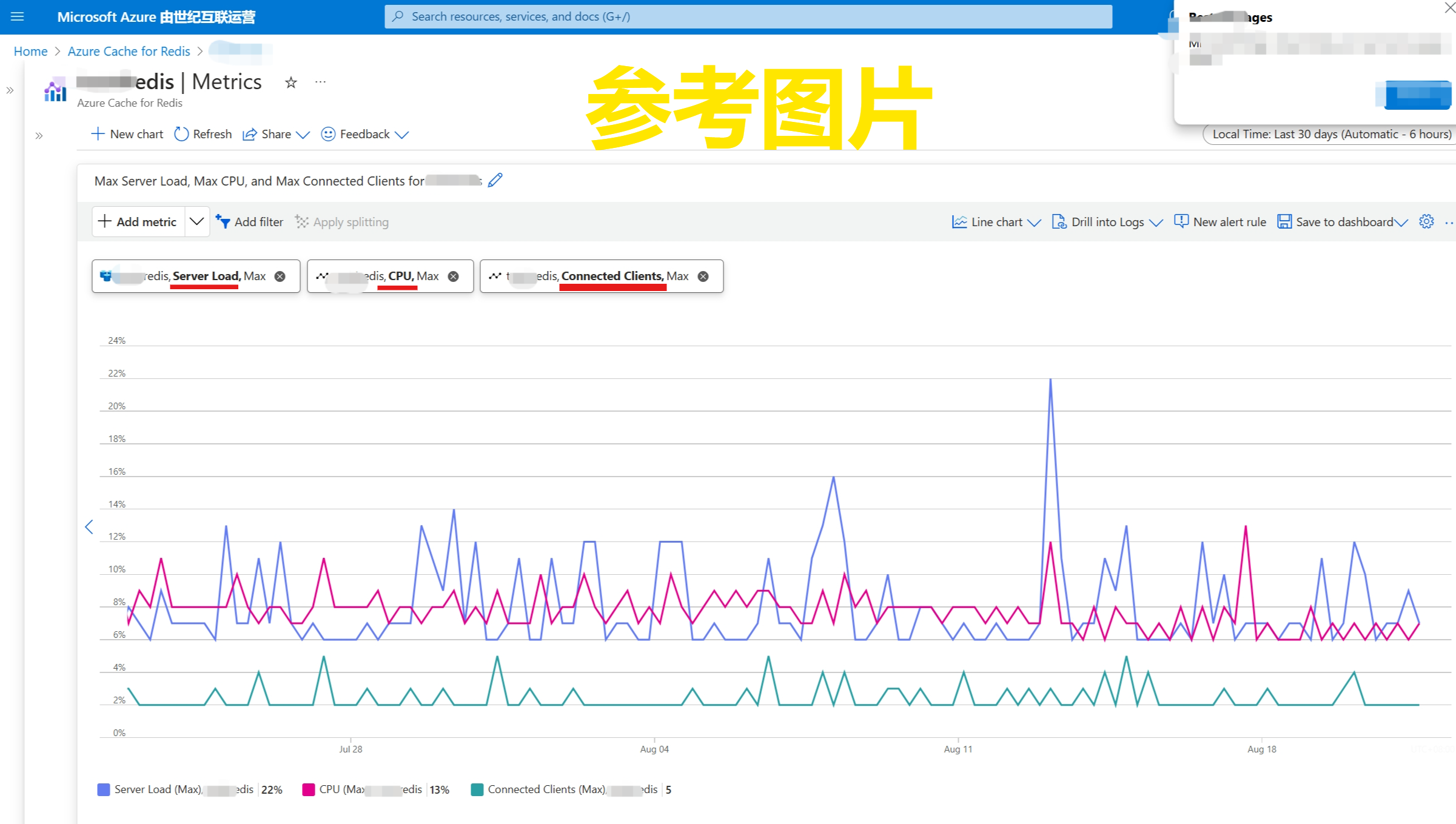
如果查看指标,并没有发现Redis服务的异常情况后,可以从一下几个方面来分析问题:
1)Azure Redis Cache的默认超时时间是10分钟,如果当前已经与Azure Redis Cache建立的连接超过10分钟没有使用,Azure Redis Cache服务端将会自动清理该连接,如果后续客户端尝试使用该已经断掉的连接去访问Azure Redis Cache,就需要重新建立连接。 详情请见:https://docs.azure.cn/zh-cn/azure-cache-for-redis/cache-best-practices-connection#idle-timeout
2)Lettuce 客户端连接Redis服务,当与服务之间的网络连接出现异常时,会导致客户端15分钟左右时间的Timeout 的已知问题
Lettuce开源社区中的相关问题讨论( https://github.com/lettuce-io/lettuce-core/issues/2082 ),当Lettuce底层TCP连接与Redis Server实际断开但客户端依然保持socket端口开放的时候,底层KeepAlive 以及Lettuce本身的保活机制不会生效,从而导致底层TCP连接成为orphan connection,进而导致Socket 依靠OS 底层tcp_retries 机制完成探测,在TCP重传15次后(大致15分钟)进行Redis连接的重新建立。
优化建议:在6.2.7.RELEASE 后 可以通过 SocketOptions 中的TCP_USER_TIMEOUT参数设置业务最大接收的timeout时间。具体配置可以参照: https://github.com/lettuce-io/lettuce-core/issues/2082#issuecomment-1702782618
// Config TCP KeepAliveSocketOptions socketOptions = SocketOptions.builder().keepAlive(KeepAliveOptions.builder().enable().idle(Duration.ofSeconds(TCP_KEEPALIVE_IDLE)).interval(Duration.ofSeconds(TCP_KEEPALIVE_IDLE/3)).count(3).build()).tcpUserTimeout(TcpUserTimeoutOptions.builder().enable().tcpUserTimeout(Duration.ofSeconds(TCP_USER_TIMEOUT)).build()).build();
3)对于偶发性的 timed out , 常见的原因有:应用使用的连接池中的连接长时间空闲,在复用连接池中的连接时。因为平台底层的TCP Socket 已经Close,而连接池中的连接依旧保持空闲状态,进而导致客户端请求超时。
- 使用客户端重试以及keep-alive 机制,可以使得连接池中的连接保活,达到尽量减少问题的发生的可能性。
- 对于使用连接池的情况,建议把TCP keep-alive 的间隔减小到3min 以下。
参考资料
- https://github.com/lettuce-io/lettuce-core/issues/2082
- https://github.com/lettuce-io/lettuce-core/issues/2082#issuecomment-1702782618
- https://docs.azure.cn/zh-cn/azure-cache-for-redis/cache-best-practices-connection#idle-timeout