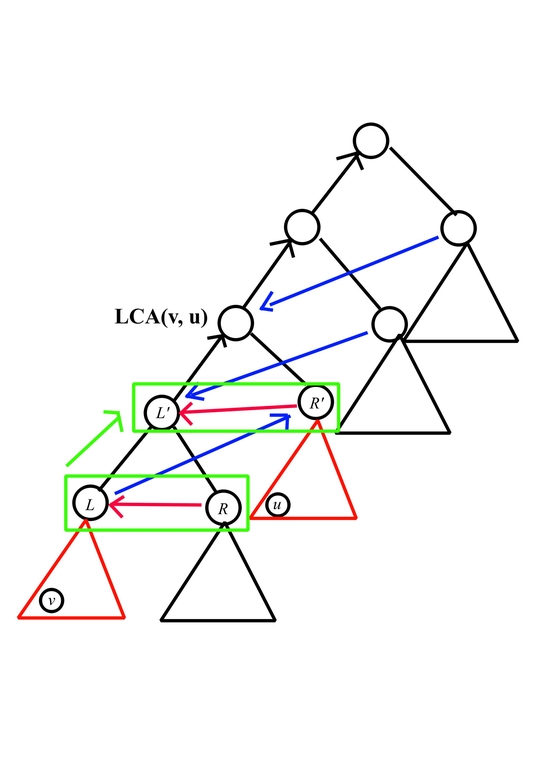
非常好的一道理解LCS本质的题目
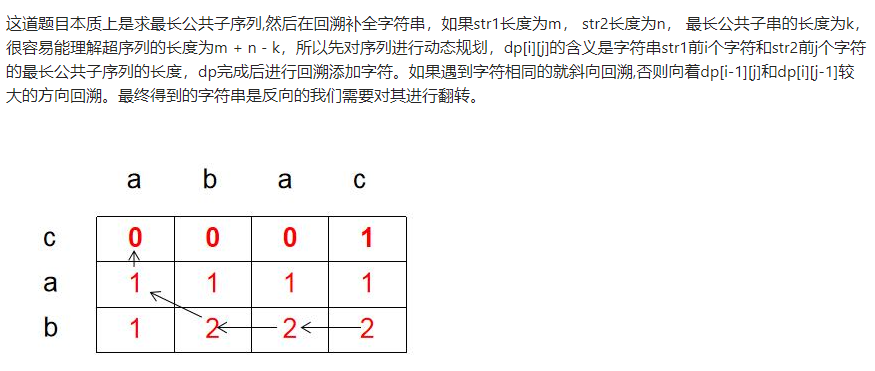
class Solution {
public:string longestCommonSubsequence(const string str1, const string str2) {int m = str1.length();int n = str2.length();// 创建一个二维数组来存储LCS的长度vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));// 填充dp数组for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {if (str1[i - 1] == str2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}// 从dp数组中构建LCSint i = m, j = n;string lcs;while (i > 0 && j > 0) {if (str1[i - 1] == str2[j - 1]) {lcs.push_back(str1[i - 1]);--i;--j;} else if (dp[i - 1][j] > dp[i][j - 1]) {lcs.push_back(str1[i - 1]);--i;} else {lcs.push_back(str2[j- 1]);--j;}}while(j>0){lcs.push_back(str2[j- 1]);--j;}while(i>0){lcs.push_back(str1[i- 1]);--i;}// 由于我们是从后往前构建LCS,所以需要反转字符串reverse(lcs.begin(), lcs.end());return lcs;}string shortestCommonSupersequence(string str1, string str2) {return longestCommonSubsequence(str1,str2); }
};