扫描线是线段树的典型应用。这玩意不难,用途也比较狭窄,重点在理解思想。
例 0 【模板】扫描线
题意
求 \(n\) 个四边平行于坐标轴的矩形的面积并。
对于 \(100\%\) 的数据,\(1 \le n \le {10}^5\),\(0 \le x_1 < x_2 \le {10}^9\),\(0 \le y_1 < y_2 \le {10}^9\)。
解析
如果用暴力法求,先单独求出每个矩形的面积,然后把所有矩形的面积加起来减去任意两个矩形的交集,时间复杂度为 \(O(n^2)\),无法通过本题。
下面用新的方法求,也就是我们要讲的 扫描线。
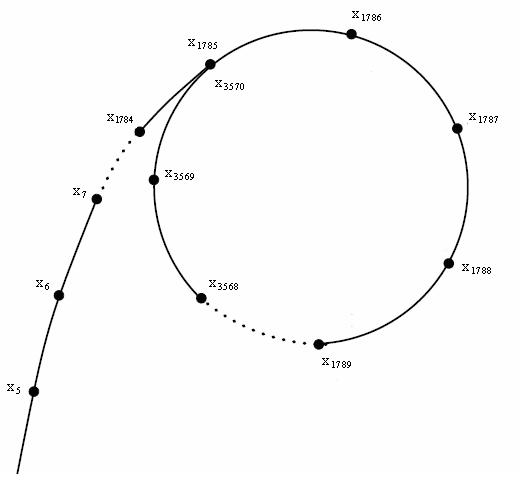
现在假设我们有一根线,从下往上开始扫描:
如图所示,我们可以把整个矩形分成如图各个颜色不同的小矩形,那么这个小矩形的高就是我们扫过的距离,只需相邻矩形纵坐标相减即可求出。那么就只剩下了一个变量,那就是矩形的长一直在变化。
我们为了维护矩形的长,我们给每一个矩形的上下边进行标记,定义下面的边为 “入边”,上面的边为 “出边”。入边标记为 \(1\),出边标记为 \(-1\)。每遇到一个入边,证明进入了一个矩形,每遇到一个出边,就证明离开了一个矩形。利用 \(1\) 和 \(-1\) 可以轻松达到这种状态。
那么这个算法如何用线段树实现?如图,我们将矩形的宽划分为了一段段小宽,遇到假如现在遇到一条入边 \([x_1,x_2]\),我们就相当于给 \([x_1,x_2]\) 这个区间 \(+1\),遇到出边则同理 \(-1\),相当于是区间和。
所以我们对读入的所有边按照纵坐标从小到大进行排序,然后一个个扫描,最后答案加上线段树根节点的值 * 矩形高度。时间复杂度 \(O(n\log n)\)。
坑点
- 每个矩形有一个入边和一个出边,所以存储边的数组要开 2 倍。
- 可见线段树维护的值域等于矩形横坐标的值域,但本题值域迭勾个 \(10^9\),所以需要离散化。
- 离散化后值域依然在 \(2\times10^5\)(别忘了有 \(2n\) 条边),再加上线段树本身需要 4 倍空间,所以线段树数组要开 8 倍。
- 如果你只是这样它依然还是个炸,需要在
pushup时特判s == t时就不要再合并左右儿子的答案了,因为它已经是叶子节点。或者,你也可以把数组再开大一点。 - 别忘了开 long long。
- 细节挺多的,一定一定要分清楚点和区间的关系,注意各种 +1-1。
实现
#include <bits/stdc++.h>
#define int long long
#define lp p << 1
#define rp p << 1 | 1
using namespace std;constexpr int MAXN = 1e5 + 5;
struct ScanLine {int y, lx, rx, io;ScanLine() {}ScanLine(int y, int lx, int rx, int io): y(y), lx(lx), rx(rx), io(io) {}friend bool operator < (ScanLine a, ScanLine b) {return a.y < b.y;}
} line[MAXN << 1];
int xx[MAXN << 1];
struct SegTree {int l, r;int tag, len;
} st[MAXN << 3];void build(int s, int t, int p) {st[p].l = s, st[p].r = t;if (s == t) return;int mid = (s + t) >> 1;build(s, mid, lp);build(mid + 1, t, rp);
}void pushup(int p) {int s = st[p].l, t = st[p].r;if (st[p].tag) st[p].len = xx[t + 1] - xx[s];else if (s == t) st[p].len = 0;else st[p].len = st[lp].len + st[rp].len;
}void update(int l, int r, int k, int p = 1) {int s = st[p].l, t = st[p].r;if (l <= s && t <= r) {st[p].tag += k;pushup(p);return;}int mid = (s + t) >> 1;if (l <= mid) update(l, r, k, lp);if (mid < r) update(l, r, k, rp);pushup(p);
}signed main() {int n, cnt = 0;int X1, X2, Y1, Y2, ans = 0;scanf("%lld", &n);while (n--) {scanf("%lld%lld%lld%lld", &X1, &Y1, &X2, &Y2);line[++cnt] = ScanLine(Y1, X1, X2, 1);xx[cnt] = X1;line[++cnt] = ScanLine(Y2, X1, X2, -1);xx[cnt] = X2;}sort(xx + 1, xx + cnt + 1);sort(line + 1, line + cnt + 1);int num = unique(xx + 1, xx + cnt + 1) - xx - 1;build(1, num, 1);for (int i = 1, l, r; i <= cnt; i++) {ans += st[1].len * (line[i].y - line[i - 1].y);l = lower_bound(xx + 1, xx + num + 1, line[i].lx) - xx;r = lower_bound(xx + 1, xx + num + 1, line[i].rx) - xx;update(l, r - 1, line[i].io);}cout << ans << '\n';return 0;
}
例 1 Atlantis
题意与例 0 相同,增加两点:坐标为小数、多测。
针对坐标为小数的情况,只需把所有和坐标有关的变量改为 double 类型即可。
针对多测,别忘清空。似乎结构体线段树在多测时建树很麻烦,换种写法就行。
例 2 [IOI1998] [USACO5.5] 矩形周长Picture
题意
给定 \(N\) 个矩形,求这些矩形的并集的周长。保证 \(1\le N<5000\),坐标值域 \(\left[-10^4,10^4\right]\)。
解析
求矩形周长并是扫描线的又一典型应用。思路相仿,但是要复杂一些,有两种方法:
- 做两次扫描。易得周长 = 横线总长 + 竖线总长,所以跑两遍扫描线即可。这种方法码量较大,我没有采用。
- 做一次扫描。其实在计算横线的同时就可以计算竖线。
把所有横线按纵坐标从小到大排序,每扫描一条横线,都计算两种值:横线和竖线。
横线的计算方法和例 0 是一样的。每次扫描,新增横线的长度 = 当前小矩形长 - 上次小矩形长。
如何计算竖线?首先,一个矩形的一条入边会有两条竖线,出边不会产生竖线;其次,如果两个矩形相邻或重叠,那么也只会产生两条竖线,而不是四条。这些竖线的长度 = 下一条横线的高度 - 当前横线的高度。
总而言之,线段树中需维护更多信息:一是当前独立线段的条数,也就是不重合的竖线条数,记为 \(\textit{num}\);而是两个布尔变量 \(\textit{lbd},\textit{rbd}\),表示当前线段的左右端点是否是独立的,目的是为了维护 \(\textit{num}\)。理解了思想后,代码容易。
坑点
- 这次的值域小,无需离散化,但开线段树的时候需要把握一下横坐标的最小值和最大值。
- 周长不同于面积,相邻的矩形会对答案产生影响。所以在排序的时候,如果两条边纵坐标相同,入边应排在出边之前,否则 WA 80pts。
实现
#include <bits/stdc++.h>
#define int long long
#define lp p << 1
#define rp p << 1 | 1
#define INF (0x3f3f3f3f)
using namespace std;constexpr int MAXN = 5005;
struct ScanLine {int y, lx, rx, io;ScanLine() {}ScanLine(int y, int lx, int rx, int io): y(y), lx(lx), rx(rx), io(io) {}friend bool operator < (ScanLine a, ScanLine b) {if (a.y == b.y) return a.io > b.io; // 精辟 return a.y < b.y;}
} line[MAXN << 1];
struct SegTree {int l, r;bool lbd, rbd;int num, tag, len;
} st[MAXN << 4];void build(int s, int t, int p) {st[p].l = s, st[p].r = t;if (s == t) return;int mid = (s + t) >> 1;build(s, mid, lp);build(mid + 1, t, rp);
}void pushup(int p) {int s = st[p].l, t = st[p].r;if (st[p].tag) {st[p].lbd = st[p].rbd = 1;st[p].len = t - s + 1;st[p].num = 1;} else if (s == t) {st[p].lbd = st[p].rbd = st[p].len = st[p].num = 0;} else {st[p].lbd = st[lp].lbd;st[p].rbd = st[rp].rbd;st[p].len = st[lp].len + st[rp].len;st[p].num = st[lp].num + st[rp].num;if (st[rp].lbd && st[lp].rbd) --st[p].num;}
}void update(int l, int r, int k, int p = 1) {int s = st[p].l, t = st[p].r;if (l <= s && t <= r) {st[p].tag += k;pushup(p);return;}int mid = (s + t) >> 1;if (l <= mid) update(l, r, k, lp);if (mid < r) update(l, r, k, rp);pushup(p);
}signed main() {int n, cnt = 0, lbd = INF, rbd = -INF;int X1, Y1, X2, Y2;scanf("%lld", &n);for (int i = 1; i <= n; i++) {scanf("%lld%lld%lld%lld", &X1, &Y1, &X2, &Y2);lbd = min(lbd, X1);rbd = max(rbd, X2);line[++cnt] = ScanLine(Y1, X1, X2, 1);line[++cnt] = ScanLine(Y2, X1, X2, -1);}sort(line + 1, line + cnt + 1);int ans = 0, last = 0;build(lbd, rbd, 1);for (int i = 1; i <= cnt; i++) {if (line[i].lx < line[i].rx) update(line[i].lx, line[i].rx - 1, line[i].io);ans += st[1].num * 2 * (line[i + 1].y - line[i].y);ans += abs(st[1].len - last);last = st[1].len;}cout << ans << '\n';return 0;
}
例 3 窗口的星星
Fleeting time does not blur my memory of you. Can it really be 4 years since I first saw you? I still remember, vividly, on the beautiful Zhuhai Campus, 4 years ago, from the moment I saw you smile, as you were walking out of the classroom and turned your head back, with the soft sunset glow shining on your rosy cheek, I knew, I knew that I was already drunk on you. Then, after several months’ observation and prying, your grace and your wisdom, your attitude to life and your aspiration for future were all strongly impressed on my memory. You were the glamorous and sunny girl whom I always dream of to share the rest of my life with. Alas, actually you were far beyond my wildest dreams and I had no idea about how to bridge that gulf between you and me. So I schemed nothing but to wait, to wait for an appropriate opportunity. Till now — the arrival of graduation, I realize I am such an idiot that one should create the opportunity and seize it instead of just waiting.
These days, having parted with friends, roommates and classmates one after another, I still cannot believe the fact that after waving hands, these familiar faces will soon vanish from our life and become no more than a memory. I will move out from school tomorrow. And you are planning to fly far far away, to pursue your future and fulfill your dreams. Perhaps we will not meet each other any more if without fate and luck. So tonight, I was wandering around your dormitory building hoping to meet you there by chance. But contradictorily, your appearance must quicken my heartbeat and my clumsy tongue might be not able to belch out a word. I cannot remember how many times I have passed your dormitory building both in Zhuhai and Guangzhou, and each time aspired to see you appear in the balcony or your silhouette that cast on the window. I cannot remember how many times this idea comes to my mind: call her out to have dinner or at least a conversation. But each time, thinking of your excellence and my commonness, the predominance of timidity over courage drove me leave silently.
Graduation, means the end of life in university, the end of these glorious, romantic years. Your lovely smile which is my original incentive to work hard and this unrequited love will be both sealed as a memory in the deep of my heart and my mind. Graduation, also means a start of new life, a footprint on the way to bright prospect. I truly hope you will be happy everyday abroad and everything goes well. Meanwhile, I will try to get out from puerility and become more sophisticated. To pursue my own love and happiness here in reality will be my ideal I never desert.
Farewell, my princess!
If someday, somewhere, we have a chance to gather, even as gray-haired man and woman, at that time, I hope we can be good friends to share this memory proudly to relight the youthful and joyful emotions. If this chance never comes, I wish I were the stars in the sky and twinkling in your window, to bless you far away, as friends, to accompany you every night, sharing the sweet dreams or going through the nightmares together.
题意
天空中有很多星星(看作平面直角坐标系),已知每个星星的坐标和亮度(都是整数)。求用宽为 \(w\)、高为 \(h\) 的矩形(\(w,h\) 为正整数)能围住的星星的亮度总和最大是多少(矩形边界上的星星不算)。
解析
截原题的题目背景是有原因的。
将星星转化为矩形,问题转化为:平面上有若干个区域,每个区域都有一个权值,求在哪个坐标上重叠的区域权值和最大。
但由于 “矩形边界上的星星不算”,为了处理边界,我们作以下假设:将所有星星的坐标向左、向下各移动 \(0.5\) 的距离,坐标从 \((x,y)\) 变为 \((x-0.5,y-0.5)\)。不妨设圈住星星的矩形顶点坐标都是整数,于是每个区域的左下角可看作 \((x,y)\),右上角可看作 \((x+w-1,y+h-1)\),边界也算在内。易证这些假设不会影响答案。
于是我们用扫描线算法,维护区间最大值即可。剩下的内容不是难点,看代码即可理解。
AC Code