语言模型与神经网络
语言模型（Language Model）
Chat GPT 流畅的语言生成能力
自然语言是一种上下文相关的信息表达和信息传递方式。
定义：语言模型是衡量一句话出现在自然语言中的概率的模型。
数学形式上，给定一句话 \(s=\{w_1,\dots,w_n\}\) ，它对应的概率为：
\[\begin{align}
\mathrm{P}(s) &= \mathrm{P}(w_1,\dots,w_n) \\
&= \mathrm{P}(w_1)\times \mathrm{P}(w_2|w_1) \times \dots \times \mathrm{P}(w_n|w_1,\dots ,w_{n-1}) \\
&= \prod_{i=1}^n\mathrm{P}(w_i|w_1,\dots,w_{i-1})
\end{align}
\]
语言模型的核心在于根据前文预测下一个词出现的概率。
如何计算语言模型的概率？
统计语言模型
马尔科夫假设：当前词出现的概率之和它前面的k个词相关。
\[\begin{align}
\mathrm{P}(w_i|w_1,\dots,w_{i-1})
&= \mathrm{P}(w_i|w_{i-k},\dots,w_{i-1}) \tag{马尔可夫假设}\\
&= \mathrm{P}(w_i) \tag{k=0, Unigram Model}\\
&= \mathrm{P}(w_i|w_{i-1}) \tag{k=1, Bigram Model}\\
&= \mathrm{P}(w_i|w_{i-2},w_{i-1}) \tag{k=2, Trigram Model}
\end{align}
\]
用频率估计概率
\[\begin{align}
\mathrm{P}(w_i|w_1,\dots,w_{i-1})
&= \mathrm{P}(w_i|w_{i-k},\dots,w_{i-1}) \tag{马尔可夫假设}\\
&= \frac{\mathrm{P}(w_{i-k},\dots,w_{i-1},w_i)}{\mathrm{P}(w_{i-k},\dots,w_{i-1})} \tag{条件概率}\\
&\approx \frac{\mathrm{count}(w_{i-k},\dots,w_{i-1},w_i)/\mathrm{count}(all~grams)}{\mathrm{count}(w_{i-k},\dots,w_{i-1})/\mathrm{count}(all~grams)} \\
&= \frac{\mathrm{count}(w_{i-k},\dots,w_{i-1},w_i)}{\mathrm{count}(w_{i-k},\dots,w_{i-1})} \tag{概率估计, N gram Model}
\end{align}
\]
语言模型评价方法
-
困惑度(Perplexity)
- 用来度量一个概率分布或概率模型预测样本的好坏程度；
- 可以用来比较两个概率模型，低困惑度的概率模型能更好地预测样本。
在测试数据上
\[\begin{align}
\mathrm{Perplexity}(s)
&=2^{H(s)} \\
&=2^{-\frac{1}{n}\log_2\mathrm{P}(w_1,\dots,w_n)} \\
&=2^{\log_2\mathrm{P}(w_1,\dots,w_n)^{-\frac{1}{n}}} \\
&=\mathrm{P}(w_1,\dots,w_n)^{-\frac{1}{n}} \\
&=\sqrt[n]{1/\mathrm{P}(w_1,\dots,w_n)}
\end{align}
\]
参数规模问题：随着k的增大，参数数目呈指数增长，无法储存。
神经网络（Neural Network）
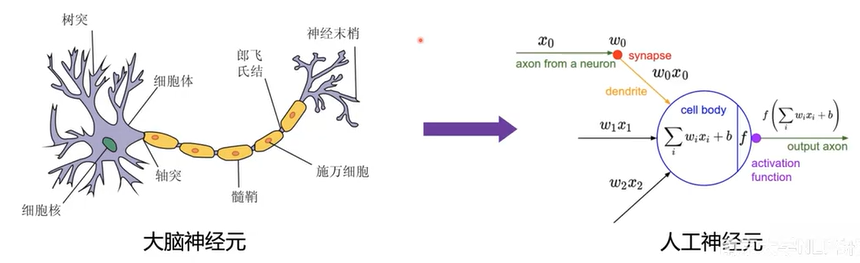
人工神经网络（Artificial Neural Network, ANN）从信息处理角度对人脑神经元网络进行抽象，建立某种算法数学模型，从而达到处理信息的目的。
- 神经元之间进行连接，组成网络；
- 网络通常是某种算法或者函数的逼近，也可能是一种逻辑策略的表达。
基于4-GRAM的神经网络语言模型
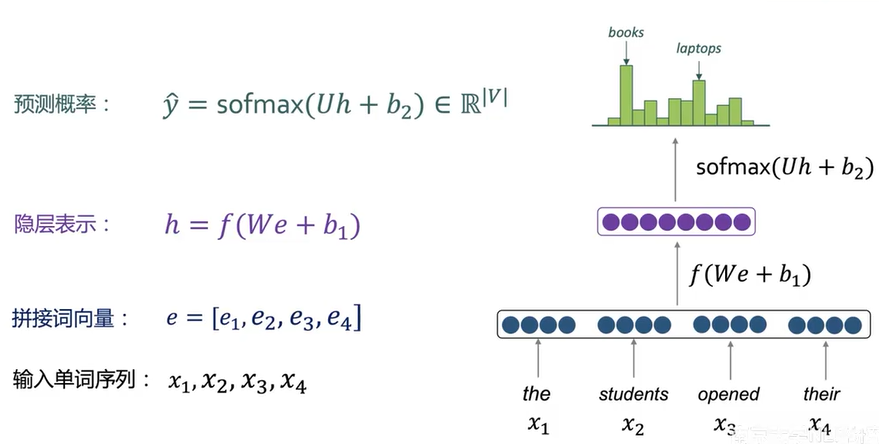
优点：
- 不会有稀疏性问题；
- 不需要存储所有的n-grams。
不足：
- 视野有限，无法建模长距离语义；
- 窗口越大，参数规模越大。
能否构建处理任意长度的神经网络模型？
循环神经网络（Recurrent Neural Network, RNN）
-
重复使用隐层参数
-
可处理任意序列长度
\[h_t = f(W_hh_{t-1} + W_xx_t + b)
\]
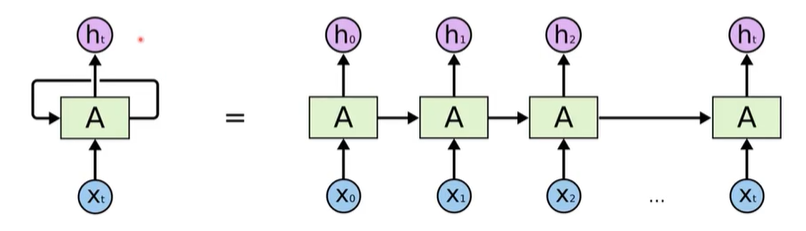
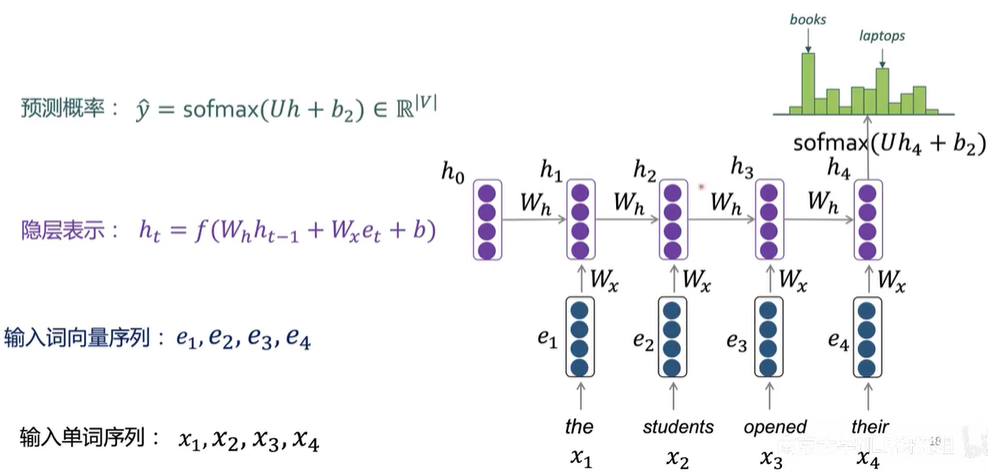
优点：
- 能处理任意长度序列；
- 能够使用历史信息；
- 模型参数量不随序列长度增加。
不足：
- 逐步计算，速度较慢；
- 长期依赖问题。
RNN-LM模型训练
- 给定长度为 \(T\) 的输入文本：\(x_1,\dots,x_T\) ；
- 将文本输入到RNN-LM，计算每一步预测的单词分布 \(\hat{y}^t\) ；
- 计算每一步预测单词的概率分布 \(\hat{y}_t\) 和真实单词 \(y_t\)（one-hot向量）之间的交叉熵：
\[\mathrm{J}^t(\theta) = \mathrm{CE}(y^t,\hat{y}^t) = -\sum_{w\in V}y_w^t\log\hat{y}_w^t = -\log\hat{y}^t_{x_t+1}
\]
- 模型在输入文本上的训练损失为：
\[\mathrm{J}(\theta) = \frac{1}{T}\sum_{t=1}^T\mathrm{J}^t(\theta) = \frac{1}{T}\sum_{t=1}^T-\log\hat{y}^t_{x_t+1}
\]
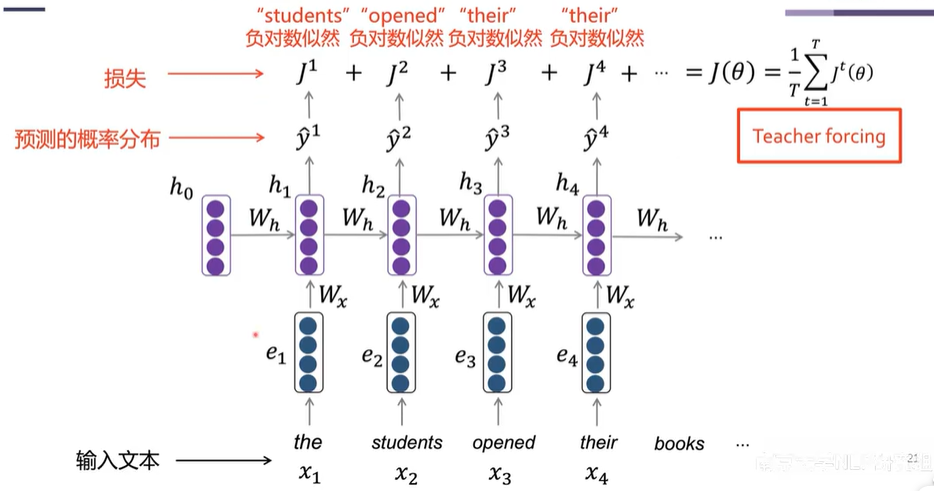
RNN：梯度爆炸、梯度消失
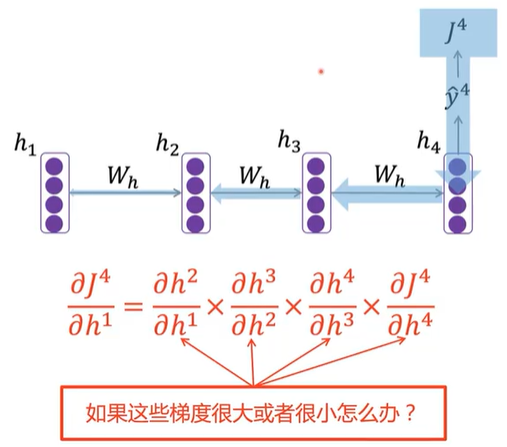
长短期神经网络（Long Short-Term Memory, LSTM）
引入三个门和一个细胞状态来控制神经元的信息流动：
- 遗忘门 \(f_t\) ：控制哪些信息应该从之前的细胞状态中遗忘；
- 输入门 \(i_t\) ：控制哪些信息应该被更新到细胞状态中；
- 输出门 \(o_t\) ：控制哪些信息应该被输出到隐层状态中；
- 细胞状态 \(C_t\) ：容纳神经元信息。
\[\begin{align}
f_t &= \sigma(W_fh_{t-1} + U_fx_t + b_f)\\
i_t &= \sigma(W_ih_{t-1} + U_ix_t + b_i)\\
o_t &= \sigma(W_oh_{t-1} + U_ox_t + b_o)\\
\hat{C}_t &= \tanh(W_ch_{t-1} + U_cx_t + b_c)\\
C_t &= f_t \times C_{t-1} + i_t \times \hat{C}_t\\
h_t &= o_t \times \tanh(C_t)
\end{align}
\]
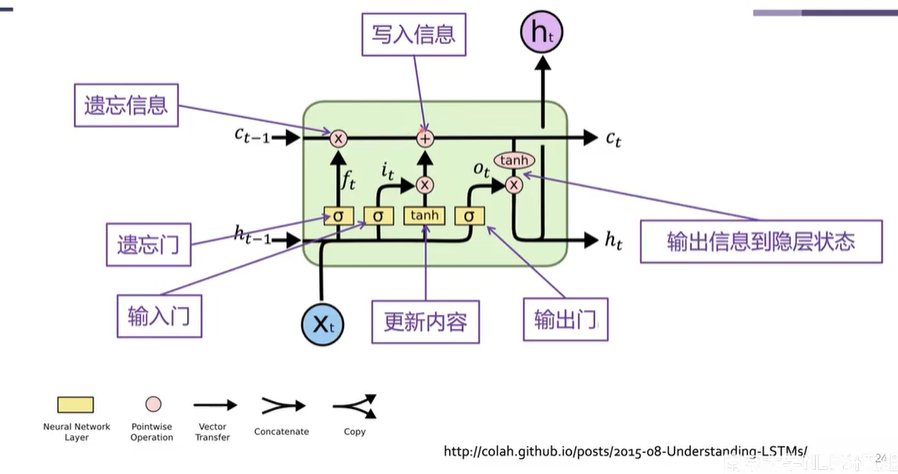
线性变换，缓解远程梯度爆炸和梯度消失问题。
Attention机制（Attention Mechanism）
神经机器翻译（Neural Machine Translation）
- 用端到端（end-to-end）的神经网络来求解机器翻译任务。
- 编码器-解码器框架（Encoder-decoder）：
- Seq2Seq；
- 编码器（encoder）：用来编码源语言的输入；
- 解码器（decoder）：用来生成目标语言的输出。
编码器-解码器框架
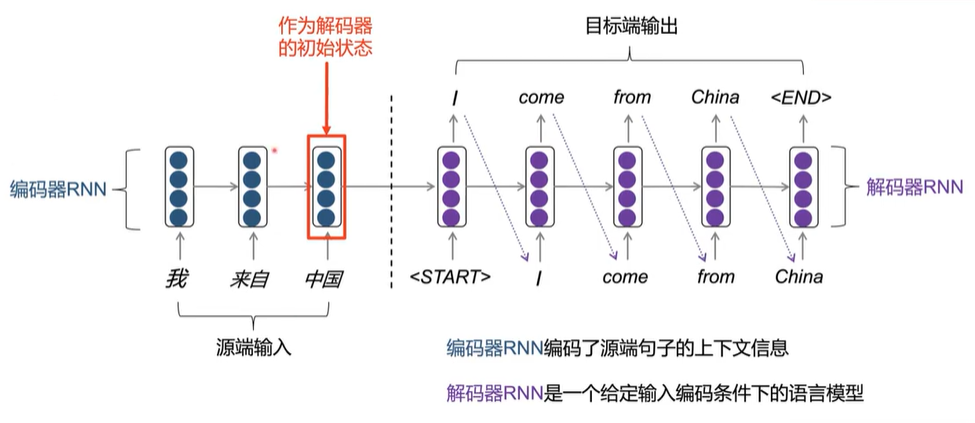
通用性：
- 文本摘要（Summarization）：长文本 \(\rightarrow\) 短文本；
- 对话生成（Dialogue generation）：之前的对话 \(\rightarrow\) 下一句对话；
- 代码生成（Code generation）：自然语言 \(\rightarrow\) 编程代码；
- \(\dots\dots\)
前后依赖性太强，且翻译过程不具有可解释性！
目标端解码某个特定单词时，应该重点关注源端相关的单词。
注意力机制
Attention Mechanism [Bahdanau et al., 2015]
- 目标端解码时，直接从源端句子捕获对当前解码有帮助的信息，从而生成更相关、更准确的解码结果。
优点：
- 缓解RNN中的信息瓶颈问题；
- 缓解长距离依赖问题；
- 具有一定的可解释性。
基于注意力机制的编码器-解码器框架
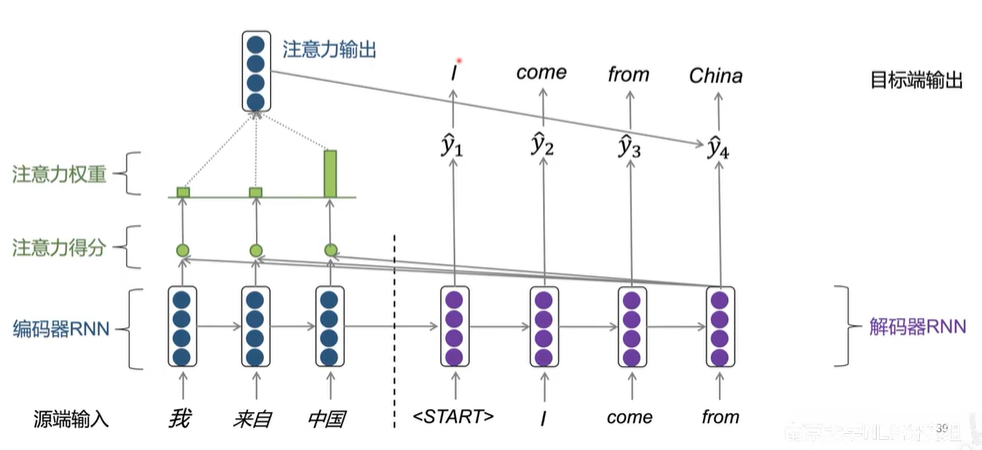
编码器-解码器中如何计算注意力？
- 编码器的隐层状态为 \(h_1,\dots,h_w\in \R^h\)
- \(t\) 时刻，解码器的隐层状态为 \(s_t\in\R^h\)
- 对于 \(t\) 时刻，编码器隐层状态的注意力打分为：
\[e^t = \big[s_t^Th_1,\dots,s_t^Th_N\big]\in\R^N
\]
- 利用softmax函数将注意力打分转换成概率化的注意力权重：
\[\alpha^t=\mathrm{softmax}(e^t)\in\R^N
\]
- 利用注意力权重α得到编码器隐层状态的加权输出：
\[a^t = \sum_{i=1}^N\alpha_i^th_i\in\R^h
\]
机器翻译中的注意力可视化
基于注意力机制的文本分类模型
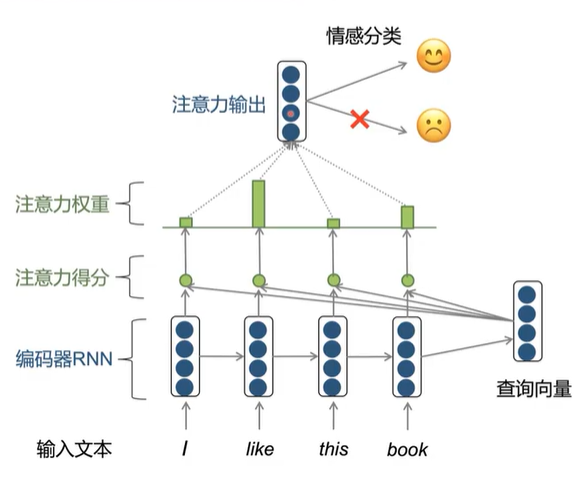
文本分类模型注意力可视化
视觉问答中的注意力
Transformer网络
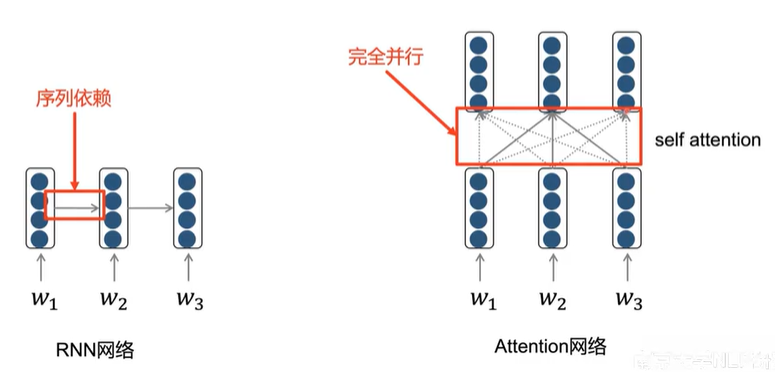
循环神经网络的问题
有限的信息交互距离：
- RNN能捕捉局部信息，但无法很好地解决长距离依赖关系（long-distance
dependency）； - 不能很好地建模序列中的非线性结构关系。
无法并行：
- RNN的隐层状态具有序列依赖性；
- 时间消耗随序列长度的增加而增加。
Self Attention
Attention Is All You Need
Transformer [Vaswani et al., 2017]
- 完全基于attention机制构建的神经网络模型；
- 直接建模输入序列的全局依赖关系；
- 并行计算。
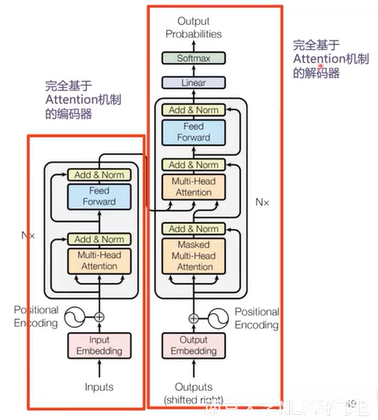
Transformer编码器
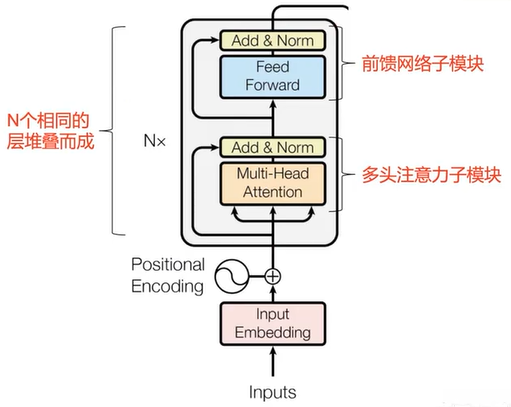
- 输入编码 + 位置编码；
- 多头注意力机制；
- 残差连接 & 层正则；
- 前馈神经网络；
- 残差连接 & 层正则。
位置编码
为什么需要位置编码？
- 注意力计算：加权和；
- 无法考虑相对位置关系。
将位置编码 \(p_i\) 注入到输入编码中：\(x_i=x_i+p_i\)
- 三角函数表示：直接根据正弦函数计算位置编码，不需要从头学习，直接计算得出。
\[p_i=\left[\begin{matrix}
sin(i/10000^{2\times1/d})\\
cos(i/10000^{2\times1/d})\\
\vdots \\
sin(i/10000^{2\times d/d})\\
cos(i/10000^{2\times d/d})\\
\end{matrix}
\right]
\]
- 从头学习：随机初始化位置编码 \(p_i\) ，并跟随网络一起训练，能更好地拟合数据。
自注意力机制
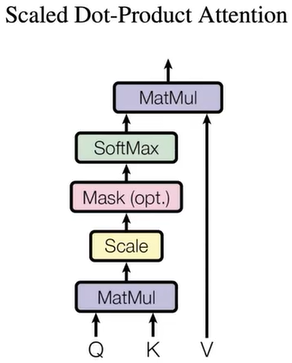
- 计算attention所需要的queries，keys，values：
\[Q = XW_Q\quad K = XW_K\quad V = XW_V
\]
- 根据queries和keys计算attention打分 \(E\) ：
\[E = QK^T
\]
- 计算attention权重 \(A\) ：
\[A = \mathrm{softmax}\Big(\frac{E}{\sqrt{d_k}}\Big)
\]
- 根据attention权重 \(A\) 和values计算attention输出 \(O\) ：
\[O = AV
\]
多头自注意力机制
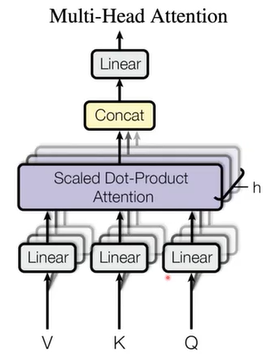
- 并行地计算多个自注意力过程，并拼接输出结果：
\[O_i = \mathrm{softmax}\Big(\frac{Q_iK_i^T}{\sqrt{d_k}}\Big)V_i \\
O = \big[O_1,\dots,O_M\big]
\]
残差连接
Residual connections [He et al., 2016]
- 将浅层网络和深层网络相连，有利于梯度回传；
- 使深处网络的训练变得更加容易。
\[X^l = \mathrm{MultiHeadAttn}(X^{l-1}) + X^{l-1}
\]
层正则
Layer Normalization [Ba et al., 2016]
- 对输入进行标准化；
- 加速收敛，提升模型训练的稳定性。
\[均值:\mu^l = \frac{1}{d}\sum_{i=1}^dx_i^l \\
方差:\sigma^l = \sqrt{\frac{1}{d}\sum_{i=1}^d(x_i^l-\mu^l)^2} \\
归一化:x'^l = \frac{x^l-\mu^l}{\sigma^l}
\]
前馈网络
两层前馈神经网络
\[\mathrm{FFN}(X) = \max(0,XW_1 + b_1)W_2 + b_2
\]
Transformer解码器
- Cross Attention：解码时需要关注源端信息。
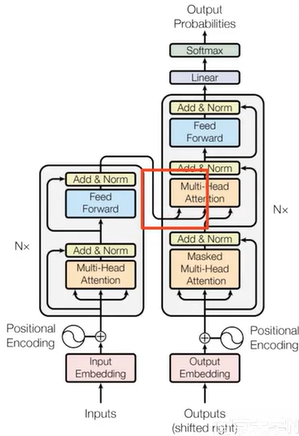
- Masked Attention：解码时（训练）不应该看到未来的信息。
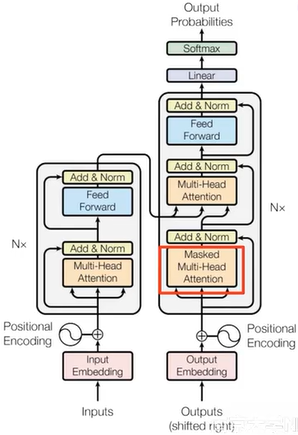
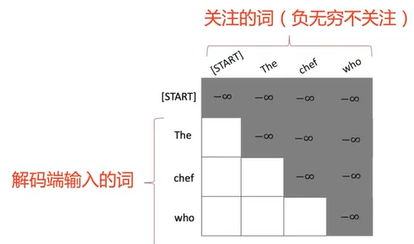
Transformer
- 机器翻译
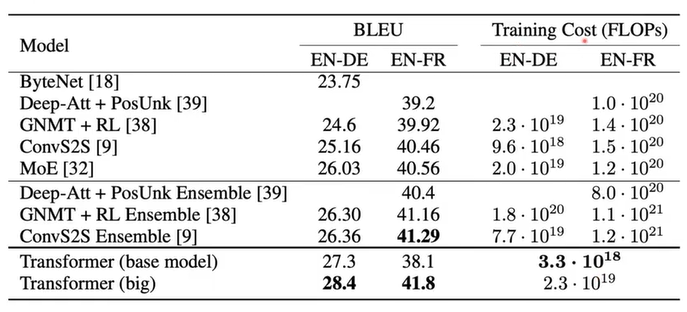
- 图像领域
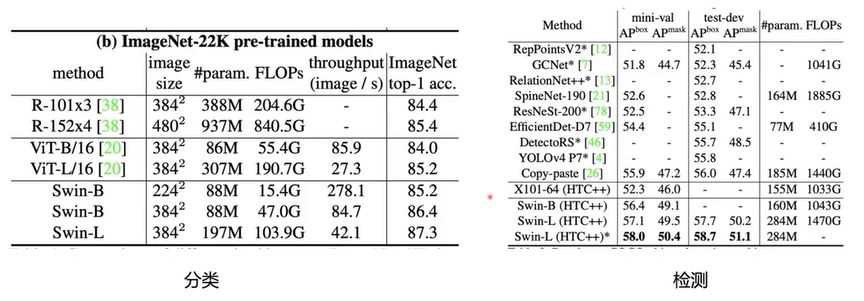
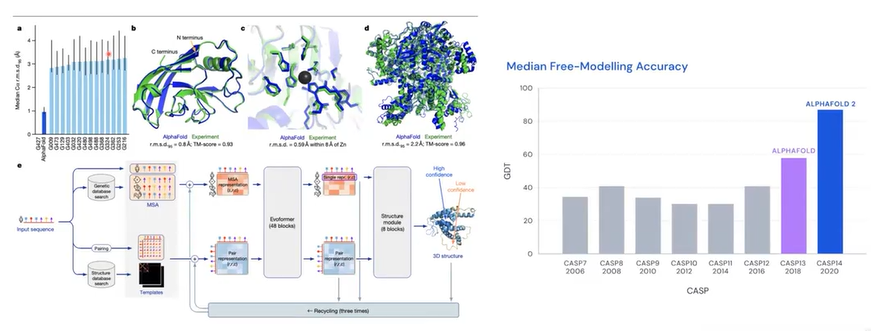
- Alphafold2
