Datawhale X 李宏毅苹果书AI夏令营 Task1打卡

3.1 局部极小值与鞍点

3.1.1 临界点及其分类

• 参数对于损失函数的微分为零时，就无法进一步优化了，训练即停止了。所以我们把这些梯度为零的点统称为临界点 。
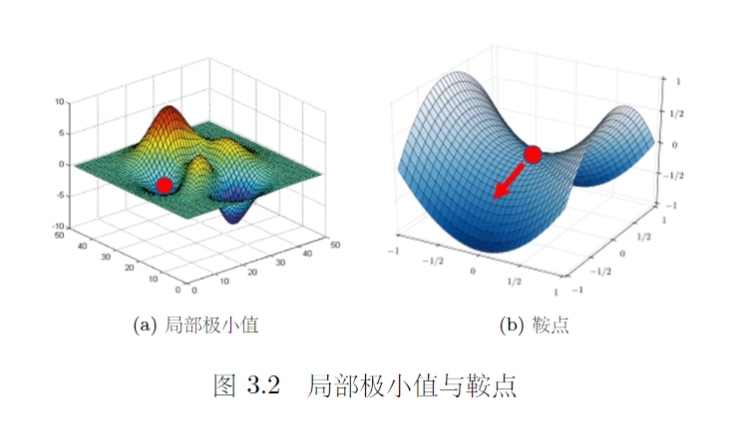
• 临界点可以分为两类：极值点 （局部极小值）和 鞍点 。
• 鞍点就是指那些梯度为零但不是局部极小值或者局部极大值的点，因为其在损失函数的图像上的形状类似于马鞍，所以称为鞍点。
• 哦按段临界点时局部极小值还是鞍点是一个很重要的问题，局部极小值点的损失无法再降低，但是鞍点还是可以进行进一步优化来降低损失的

3.1.2 判断临界值种类的方法

对于复杂网络来说，整个损失函数的形状可能也非常复杂，我们无法知道整个损失函数的形状，但是我们可以利用 泰勒级数近似 的方式来得到某个点附近的损失函数的大概形状。假设给定某一组参数 \(\theta^{\prime}\) ，对于该点附近的任意一点 \(\theta\) 来说，其损失函数 \(L(\theta)\)

\[L(\theta) = L(\theta^{\prime})+(\theta-\theta^{\prime})^T g + \frac{1}{2}(\theta-\theta^{\prime})^T H(\theta-\theta^{\prime}) \]

其中 \(g\) 表示梯度 \(\nabla L(\theta^{\prime})\) ，\(H\) 表示海森矩阵（即二次微分形式）

对于临界点来说梯度 \(g\) 为零，因此我们需要通过最后一项来判断该临界点时局部最小值，局部最大值还是鞍点。用向量 \(v\) 来表示 \(\theta-\theta^{\prime}\) :

1. 若对于所有的 \(v\) 来说，\(v^THv > 0\) 则 \(\theta^{\prime}\) 是局部极小值
2. 若对于所有的 \(v\) 来说，\(v^THv < 0\) 则 \(\theta^{\prime}\) 是局部极大值
3. 若 \(v^THv\) 既可以为正值也可以为负值，则该点是鞍点
   但是很明显，我们不可能将所有的 \(v\) 代入来检验。因此借助线性代数的知识我们可以知道，上述问题可以转化为判断海森矩阵 \(H\) 的正定性，若海森矩阵是正定的即是局部最小值，若海森矩阵是负定的则是局部最大值，否则为鞍点。

在了解了如何判断临界点种类后，我们需要知道对于一个鞍点应该如何更新参数。设 \(\lambda\) 是 \(H\) 的一个特征值，其对应的特征向量是 \(u\) ，则令 \(\theta - \theta^{\prime} = u\) 则

\[u^THu = u^T(\lambda u)= \lambda \lVert u\rVert^2 \]

当特征值 \(\lambda\) 为负时，上式恒为负值，因此可以沿着负特征值对应的特征向量的方向去更新参数，损失就会降低

3.1.3 逃离鞍点的方法

通过先前的分析和计算，我们已经得到了一种判断鞍点并且更新参数的方法。但是很显然，对于一个复杂的神经网络和损失函数来说，计算海森矩阵和其特征值是一个非常麻烦的事情。所以我们退一步来想，是否有必要对于每一个临界点都判断一下其是否是鞍点？并且计算其负特征值对应的特征向量？

观察损失函数的图像可以看出，对于一个鞍点，如果我们从某个特定的界面来看这个鞍点可能就是一个低一维的局部极小值。因此我们可以自然地猜想，当参数量增大时是否有很多低维的局部极小值就会变成鞍点。即对于一个复杂的神经网络（参数量非常大）来说我们可以大胆猜想，其局部极小值点非常少，只占临界点中很小的一部分。

我们定义 最小值比例 为：

\[最小值比例 = \frac{正特征值数量}{总特征值数量} \]

由上图我们可以看出，对于神经网络我们几乎找不到极小值点，对于大部分的临界点来说，正特征值的数量不会超过 60%，因此我们训练的时候遇到梯度很小的地方，往往是遇到了鞍点。

3.2 批量和动量

在计算梯度的时候，并不是对所有的数据的损失计算梯度，而是分成一个一个的批量。在把数据分成批量的时候，我们还会进行随机打乱。随机打乱的做法也有很多，一种常见的是在每一回合开始的时候，重新随机划分批量，即每一个回合的批量数据都不一样多。

3.2.1 批量大小对梯度下降法的影响

我们可以先看两个极端的情况：

• 使用全批量的数据来更新参数，也叫做批量梯度下降法 (BGD)
• 批量大小等于1，此时使用的方法即随机梯度下降法（SGD），也成为增量梯度下降法
  随机梯度下降法引入了随机噪声，因此在非凸优化问题中，相比于批量梯度下降法更容易逃离局部最小值
  

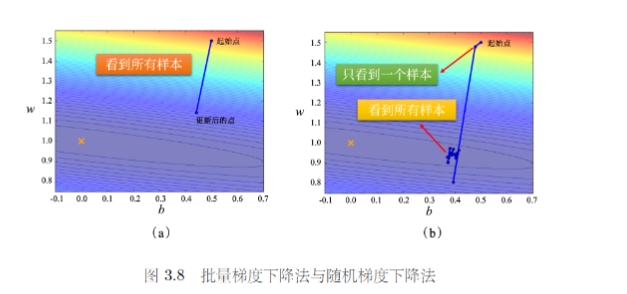
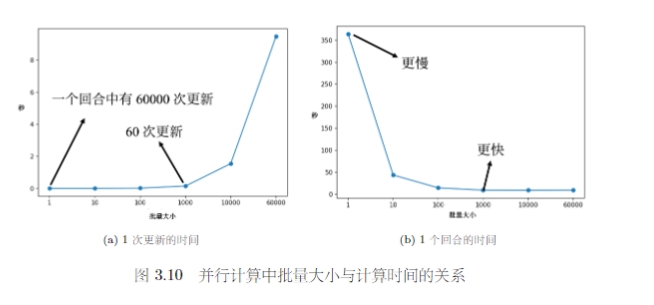
虽然批量梯度下降法每一次更新都要看完所有数据，但是实际上考虑到并行运算的形式，批量梯度下降花费的时间并不一定更长。因为在数据上计算和更新所需要的时间成本是不一样多的。因此在运行并行计算的情况下，大的批量反而可能是更有效率的。

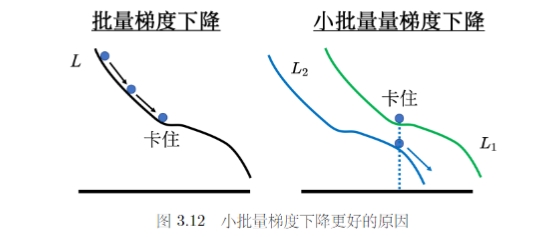
大的批量更新比较稳定，小的批量更新的梯度方向是比较有噪声的。但实际上这种噪声反而可能可以帮助训练。

一个可能的解释就是，小批量的梯度下降方式，每次计算的损失函数是有差异的，因此每次更新的方向比较随机，在某些情况下不容易被卡住。

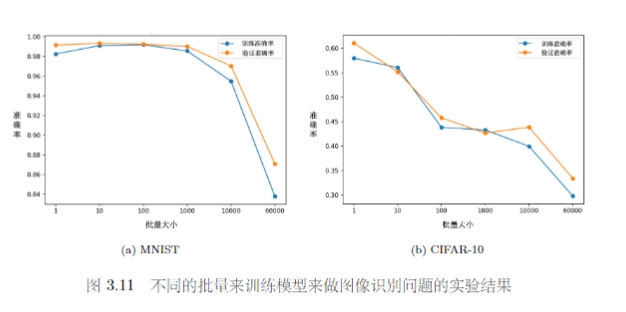
在论文 “On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima”中作者通过实验发现小批量对于测试也很有帮助。大批量和小批量的训练准确率差不多，安东尼是在测试的时候，大批量更差，表现为过拟合。论文给出了一种解释是，训练损失上有很多的局部最小值，但是局部最小值有好坏之分。小批量训练由于其更新的随机性，其往往会找到一个平坦区域的最小值，当由训练集变成测试集时这种损失的变化幅度不会很大。但是大批量若是找到了一个陡峭区域的最小值，当数据发生变化时，损失可能会出现突增导致准确率下降。

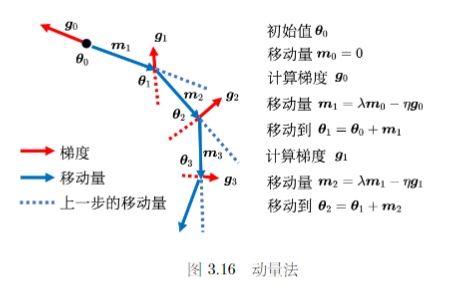
3.2.2 动量法

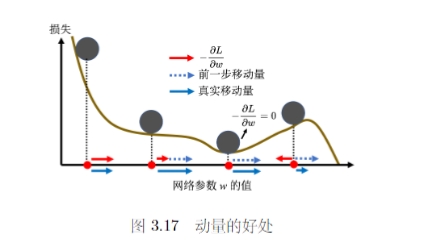
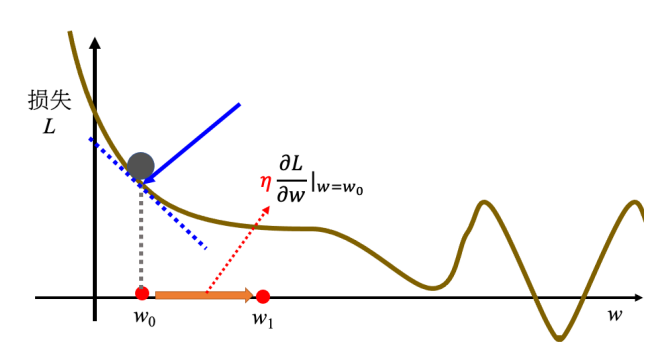
动量法是另一种可以对抗鞍点或者局部最小值的方法。类比物理世界和滚动的小球，当球从高处滚下时，遇到鞍点或者局部最小值时不一定会被卡住，可能会因为动量的存在而翻过小坡继续向前。

相比于一般的梯度下降法，每一次直接按照梯度的反方向移动来更新参数。动量法每一次更新时，还要加上前一部移动的方向，来决定新的更新方向，记 \(m_i\) 表示第 i 次的更新量，对于一般的梯度下降法 \(m_i = -\eta g_i\) 而对于动量发来说 \(m_i = \lambda m_{i-1} - \eta g_i\) （\(\lambda\) 是前一个方向的权重参数，\(\eta\) 时学习率）另一个角度理解动量法可以认为在更新时不仅需要考虑现在的梯度，而是以一定的权重考虑过去所偶有的梯度的总和，并且这种权重是逐渐累积的。