正在完善!
何为博弈论
博弈论 ,是经济学的一个分支,主要研究具有竞争或对抗性质的对象,在一定规则下产生的各种行为。博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
先来看一道小学就接触过的思维题
你和好基友在玩一个取石子游戏。面前有30颗石子,每次只能取一颗或两颗,你先取,取完的人为胜,问你是否有必胜策略
Q:什么?有必胜策略?能否胜利不应该随着我们选择而改变吗?
A:确实。但如果我们足够聪明呢?每次都做最优的选择,把取胜之路留给自己
Q:我一点也不聪明,那该如何做呢?
先从简单入手,
假如只有一个或两个石子,无疑先手必胜
只有三个石子,无疑先手必输
(我们约定先手必败状态为必败状态,先手必胜状态为必胜状态)
这就是我们的终止状态,即无论怎么拿,都会回到这几个状态
因为我们想赢,所以我们要让自己处于必胜状态,即剩下一个或两个石子的时候,我们是先手。不难发现,我们也许不能使自己处于必胜态,但我们可以让对方处于必败态。即剩下三个石子的时候,我们是后手。
不难发现,只要是三的倍数就一定是必败状态,否则就是必胜状态。
证明:
假设不是三的倍数,我们使它成为三的倍数,此时我们是后手。对方如果拿一个,我们就拿两个;如果拿两个,我们就拿一个。所以我们那完后剩下的一定永远是三的倍数,所以只剩下三个石子的时候我们一定是后手,此时对手必输,也就是我们必胜。
假设是三的倍数,因为两个人都足够聪明,所以对方一定会使我们永远处于三的倍数中。所以我们必败。
所以只要判断是不是三的倍数,就可以确定我们是否必胜了
至此,小学时代遗留的问题已经解决了可以拿去欺负同学,(这也是博弈论最基础的问题,Nim游戏)
可以说,你已经学会博弈论了
下面我主要讲一些关于算法比赛中用到的博弈类型:
首先你要理解必胜状态和必败状态:
对下先手来说,
一个状态是必败状态当且仅当它的所有后继都是必败状态。
一个状态是必胜状态当且仅当它至少有一个后继是必败状态。
就是说,博弈者,一旦捉住了胜利的把柄,必然最后胜利。
博弈中常常用到的:
两个数,不用中间变量实现交换。
a b;
a = a^b;
b = a^b;
a = a^b;
博弈图和状态
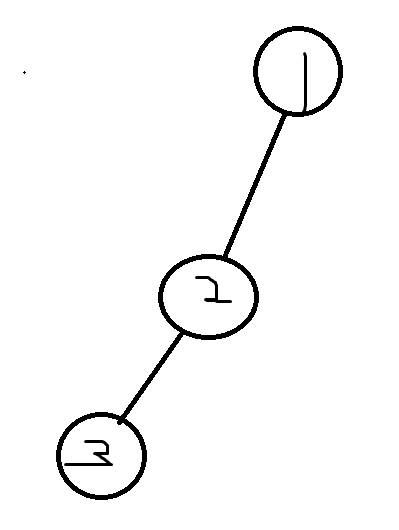
把每个可到达的状态都看做结点,每次做出决策都是从旧的状态转移到新的状态,也就是在两个状态结点间连一条有向边。如果把所有状态转移都画出来,我们就得到了一张博弈图
就像这样
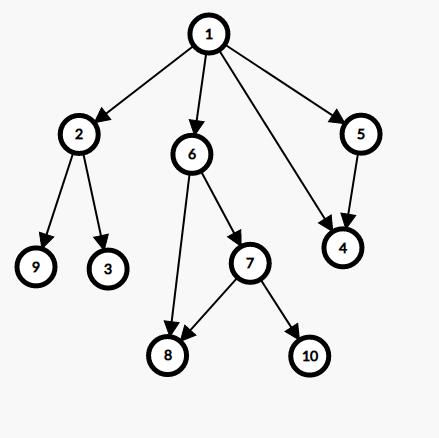
大多数博弈图会是一个DAG,否则游戏不可能结束
三个基本定理
- 定理一:没有后继状态的状态是必败状态
- 定理二:一个状态是必胜状态 当且仅当 存在至少一个必败状态为它的后继状态。
- 定理三:一个状态是必败状态 当且仅当 它的所有后继状态均为必胜状态。
对于定理一,游戏进行不下去了,即这个玩家没有可操作的了,那么这个玩家就输掉了游戏
对于定理二,如果该状态至少有一个后继状态为必败状态,那么玩家可以通过操作到该必败状态;此时对手的状态为必败状态,即对手必定是失败的,而相反地,自己就获得了胜利。
对于定理三,如果不存在一个后继状态为必败状态,那么无论如何,玩家只能操作到必胜状态;此时对手的状态为必胜状态——对手必定是胜利的,自己就输掉了游戏。
SG函数
有向图游戏是一个经典的博弈游戏——实际上,大部分的公平组合游戏都可以转换为有向图游戏。
在一个有向无环图中,只有一个起点,上面有一个棋子,两个玩家轮流沿着有向边推动棋子,不能走的玩家判负。
定义 mex 函数的值为不属于集合 S 中的最小非负整数,即:
mex(S) = min{x} ( x ∉ S , x ∈ N )
例如 mex({0,1,3,4})=1,mex({1,2})=0,mex({})=0
对于状态 x 和它的所有 k 个后继状态 y1,y2,...,yk,定义 SG 函数:
SG(x)=mex{SG(y1),SG(y2),...,SG(yk)}
SG定理:
而对于由 n 个有向图游戏组成的组合游戏,设它们的起点分别为 s1,s2,...,sn ,则有定理: 当且仅当
SG(s1)⊕SG(s2)⊕...⊕SG(sn)≠0 时,这个游戏是先手必胜的。
还是拿原来那个图开刀
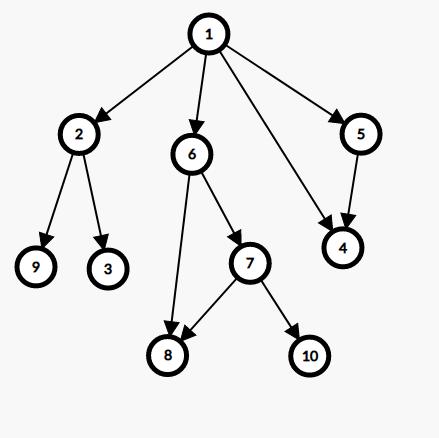
用 SG[] 数组来存所有结点的 SG 函数值因为 9,3,8,10,4 这几个点都没有后继状态,所以它们 SG 值均为 0,同理推出 2,7,5这个点的 SG 值为 1,而
SG[6]=mex(SG[7],SG[8])=2SG[1]=mex(SG[2],SG[5],SG[6],SG[4])=3
把 Nim游戏 转化为有向图游戏
我们可以将一个有 x 个物品的堆视为节点 x ,拿掉若干个石子后剩下 y个,则当且仅当 0<y<x 时,节点 x 可以到达 y 。
那么,由 n 个堆组成的 Nim 游戏,就可以视为 n 个有向图游戏了。根据上面的推论,可以得出 SG(x)=x 。
再根据 SG 定理,就可以得出 Nim 和的结论了。
博弈论DP
不得不说,博弈论DP就是个神仙做法,能有博弈论DP做的都是神仙题!
并没有什么固定的做法,但基本原理还是照着那三个定理来。能用DP的一般是因为想不出来如何用 SG 定理。状态的设计都比较神仙,主要是根据题目要求来设计。
可以参考一下下面两个博弈论DP习题找找感觉,我也不是很会,主要是学会如何去设计状态。