CCPC网络赛 G
Problem G. 疯狂星期六
Input file: standard input Output file: standard output
Time limit: 1 second Memory limit: 256 megabytes
yyq 和他的朋友们一共 n 个人(编号为 1 到 n ,yyq 编号为 1)去某饭店吃疯狂星期六。第 i 个人初始手中有 ai 元的零花钱,即每个人的总花费不能超过 ai 元。由于每个人到饭店的路程不同,所以第 i 个人打车去的花费为 Vi 元。yyq 和他的朋友们一共点了 m 件菜品。其中,第 i 件菜品价值 Wi 元,由第 xi 个人和第 yi 个人吃。结账的时候,xi 和 yi 可以自行决定他们俩谁付多少钱(要求每个人在这道菜中付的钱为非负整数,且 xi和 yi 付款的和必须为 Wi 元)。由于今天是 yyq 的生日,所以 yyq 想让自己的总花费(打车费与菜品费之和)最多,即严格大于其他每个人的总花费。
请问在每个人不超额花费的前提下, yyq 的愿望能实现吗?
注意 xi 和 yi 可能相等,即一个人独吃这道菜,这个人独自付该菜品费用。
Input
第一行,两个整数 n, m(2 ≤ n ≤ 103,1 ≤ m ≤ 103),分别表示人数和菜品数量。
接下来 n 行,每行 2 个整数 ai, Vi(1 ≤ Vi ≤ ai ≤ 106),分别表示这 n 个人的零花钱数和打车费用。
接下来 m 行,每行 3 个整数 xi, yi, Wi(1 ≤ xi, yi ≤ n ,1 ≤ Wi ≤ 106),表示这 m 件菜品的信息:第i 件菜品价值 Wi 元,由 xi 和 yi 食用并付款。(注意 xi 和 yi 可能相等)
Output
共一行。若 yyq 能实现愿望,输出 YES,否则输出 NO。
首先算出yyq能花费的最大金额,即 所有yyq吃的菜的价值总和加上yyq打车费用 和 yyq的零花钱 的最小值.
样例1建图
3 3
10 5
6 5
15 1
1 2 3
1 3 1
2 3 2
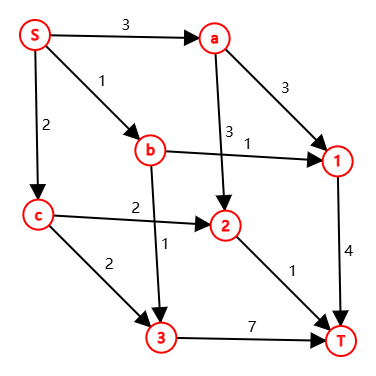
样例2建图
2 1
1 1
1 1
1 2 1
代码
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const ll inf=0x3f3f3f3f3f3f3f3f;
const ll infll=0x3f3f3f3f3f3f3f3f;
#define int long long
#define pii pair <int,int>
#define ld long double
#define endl "\n"
const int N=200050;int a[N],v[N];
int x[N],y[N];
int wei[N];struct EDGE_{int to,w,nxt;
}E_[N];
int HEAD_[N],cnt;
//链式前向星存图:HEAD[i]是i最后出现的位置,nxt是这个点为出点的上一个位置。void INIT(int n){for (int i=0;i<=n;i++)HEAD_[i]=-1;cnt=0;
}void ADD1(int u,int v,int w){E_[cnt].nxt=HEAD_[u];E_[cnt].to=v;E_[cnt].w=w;HEAD_[u]=cnt++;
}void ADD(int u,int v,int w){ADD1(u,v,w);ADD1(v,u,0);
}int S_,T_;
int NOW[N],DIS[N];
int BFS_(){memset(DIS, 0x3f,sizeof DIS);//<-注意数据范围:如果需要开ll,应该改掉infqueue<int> q;q.push(S_);DIS[S_]=0;NOW[S_]=HEAD_[S_];while (!q.empty()){int u=q.front();q.pop();for (int i=HEAD_[u];i!=-1;i=E_[i].nxt){int v=E_[i].to;if(E_[i].w>0&&DIS[v]==inf){q.push(v);NOW[v]=HEAD_[v];DIS[v]=DIS[u]+1;if(v==T_)return 1;}}}return 0;
}
int DFS_(int u,int sum){if(u==T_)return sum;int k,res=0;for (int i=NOW[u];(i!=-1)&∑i=E_[i].nxt){NOW[u]=i;int v=E_[i].to;if(E_[i].w>0&&(DIS[v]==DIS[u]+1)){k=DFS_(v,min(sum,E_[i].w));if(k==0)DIS[v]=inf;E_[i].w-=k;E_[i^1].w+=k;res+=k;sum-=k;}}return res;
}
int Dinic(){int res=0;while (BFS_()){// cerr <<1<<endl;res+=DFS_(S_,inf);}return res;//最坏时间复杂度:O(V^2·E)//单位容量(w=1)网络时间复杂度:O(E·min((E^(1/2),V^(2/3))
}
//注意要调用INIT函数
//注意数据范围能不能memset(BFS_)signed main (){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n,m;cin >>n>>m;for (int i=1;i<=n;i++){cin >>a[i]>>v[i];}int sum=0;int sumy=0;for (int i=1;i<=m;i++){int u,v,w;cin >>u>>v>>w;x[i]=u,y[i]=v,wei[i]=w;sum+=w;if (u==1||v==1)sumy+=w;}int mx=min(sumy+v[1],a[1]);a[1]=mx;for (int i=2;i<=n;i++){a[i]=min(a[i],mx-1);}for (int i=1;i<=n;i++){a[i]-=v[i];if (a[i]<0){cout <<"NO"<<endl;exit(0);}}INIT (m+n+2);S_=m+n+1,T_=m+n+2;for (int i=1;i<=m;i++){ADD(S_,i,wei[i]);}for (int i=1;i<=m;i++){if (x[i]==y[i])ADD(i,m+x[i],wei[i]);else{ADD(i,m+x[i],wei[i]);ADD(i,m+y[i],wei[i]);}}for (int i=1;i<=n;i++){ADD(i+m,T_,a[i]);}if (Dinic()==sum)cout <<"YES"<<endl;else cout <<"NO"<<endl;
}