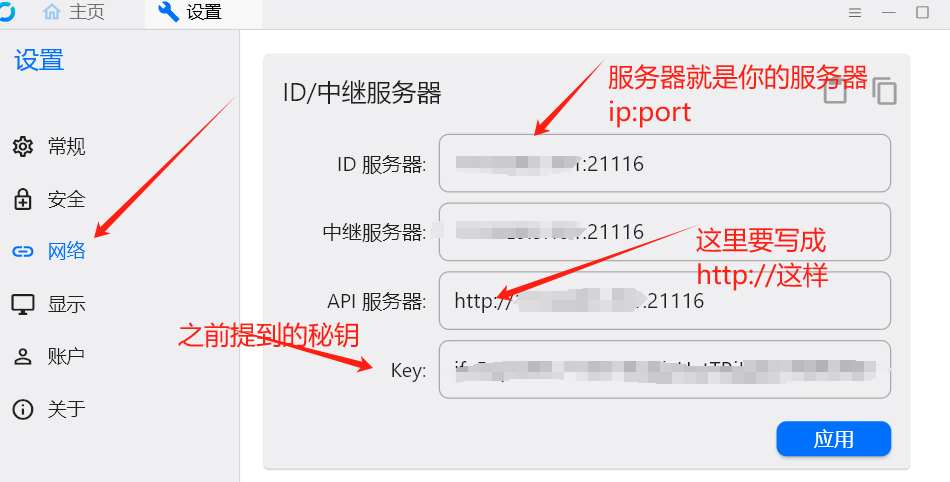
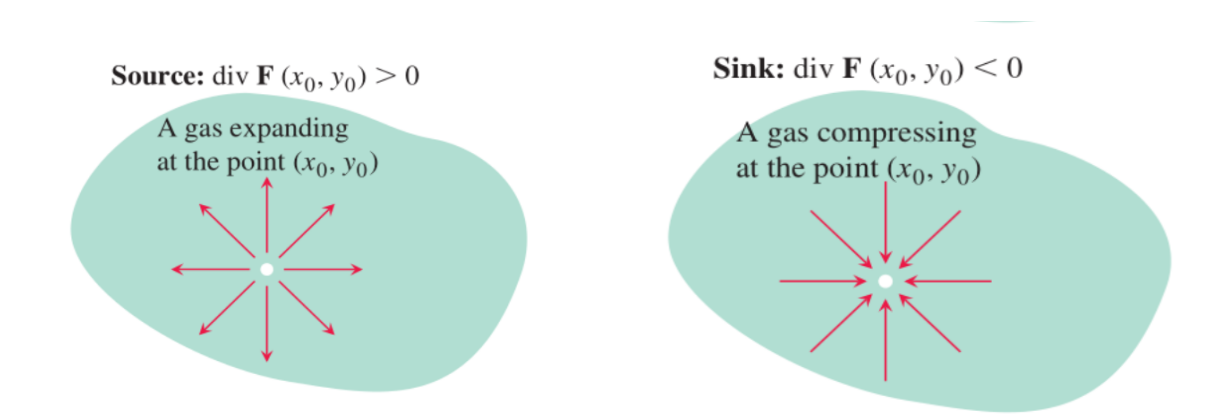二维或三维的分布积分(格林公式)
分布积分对下式积分
\[\int\int_{\Omega}\Phi\frac{\partial\Psi}{\partial x}\mathrm{d}x\mathrm{d}y
\]
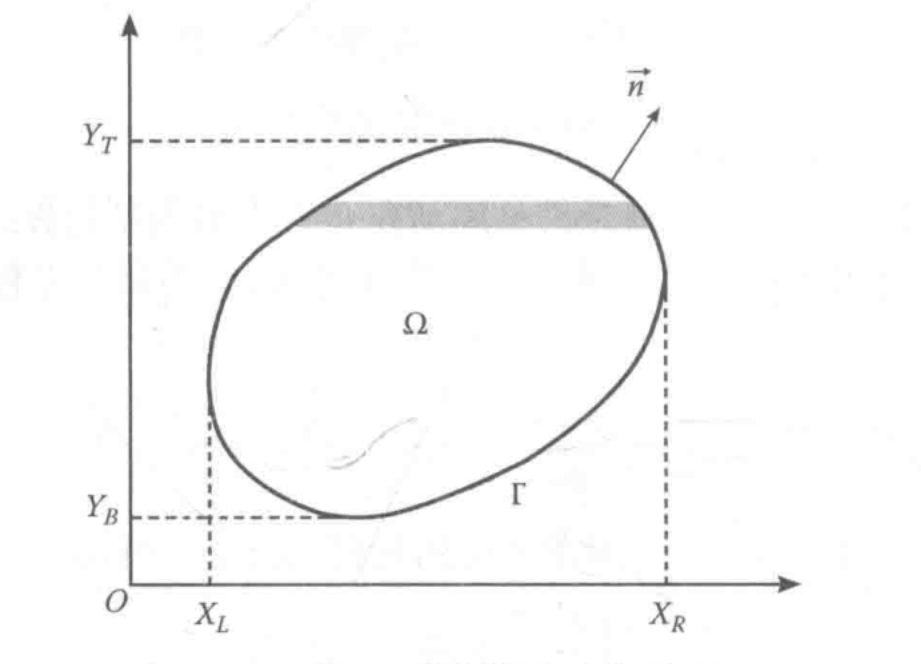
首先对变量\(x\)分布积分
\[\int\limits_{X_L}^{X_R}U\mathrm{d}V=(UV_{X=X_R}-UV_{X=X_L})-\int\limits_{X_L}^{X_R}V\mathrm{d}U
\]
对于二维问题
\[\int\int\limits_{\Omega}\Phi\frac{\partial\Psi}{\partial x}\mathrm{d}x\mathrm{d}y=-\int\int\limits_{\Omega}\frac{\partial\Phi}{\partial x}\Psi\mathrm{d}x\mathrm{d}y+\int\limits_{Y_{B}}^{Y_{T}}[(\phi\psi)_{x=X_{R}}-(\phi\psi)_{x=X_{L}}]\mathrm{d}y
\]
如果在求解边界取一个无穷小的微元,那么在求解域的左侧和右侧:
\[\mathrm{d}y=n_x\mathrm{d}\Gamma \\\mathrm{d}y=-n_x\mathrm{d}\Gamma
\]
其中 \(n_x\)是求解域边界$T \(的法矢量\)\vec{n}\(与\)x$ 轴夹角的方向余弦
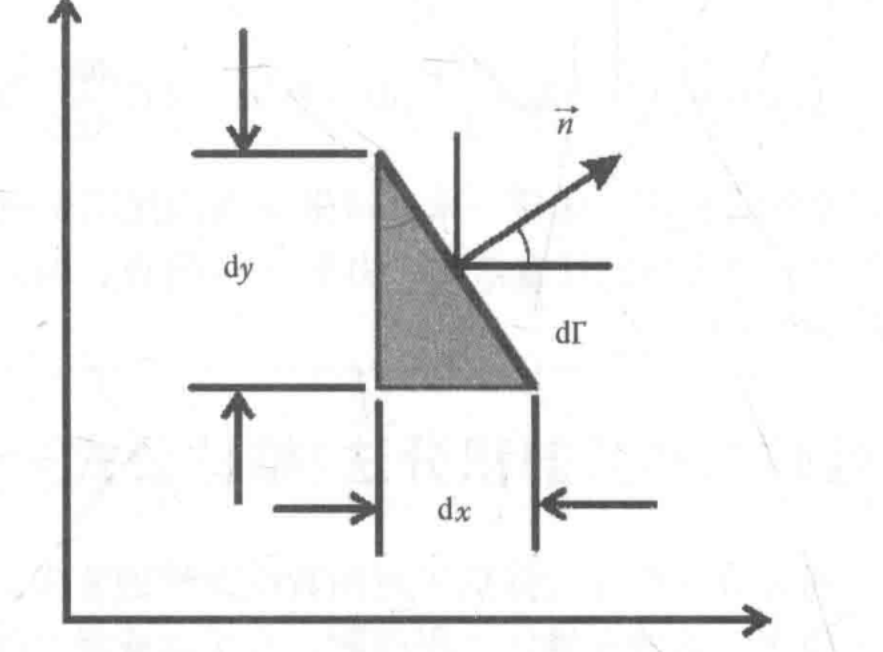
则
\[\int\int\limits_{\Omega}\Phi\frac{\partial\Psi}{\partial x}\mathrm{d}x\mathrm{d}y=-\int\int\limits_{\Omega}\frac{\partial\Phi}{\partial x}\Psi\mathrm{d}x\mathrm{d}y+\int\limits_{Y_{B}}^{Y_{T}}[(\phi\psi)_{x=X_{R}}-(\phi\psi)_{x=X_{L}}]\mathrm{d}y
\]
上式右边的定积分部分可以写成曲线积分形式
\[\oint_{\Gamma}\Phi\Psi n_x\mathrm{d}\Gamma
\]
则
\[\int\int_{\Omega}\Phi\frac{\partial\Psi}{\partial x}\mathrm{d}x\mathrm{d}y
\]
可表示为
\[\int\int_{\Omega}\Phi\frac{\partial\Psi}{\partial x}\mathrm{d}x\mathrm{d}y=-\int\int_{\Omega}\frac{\partial\Phi}{\partial x}\Psi\mathrm{d}x\mathrm{d}y+\oint_{\Gamma}\Phi\Psi n_{x}\mathrm{d}\Gamma
\]
同理,如何沿\(y\)积分可得
\[\int\int\limits_{\Omega}\Phi\frac{\partial\Psi}{\partial y}\mathrm{d}x\mathrm{d}y=-\int\int\limits_{\Omega}\frac{\partial\Phi}{\partial y}\Psi\mathrm{d}x\mathrm{d}y+\oint\limits_{\Gamma}\Phi\Psi n_y\mathrm{d}\Gamma
\]
\(\Gamma\)表示曲面,而\(\Omega\) 表示三维求解域
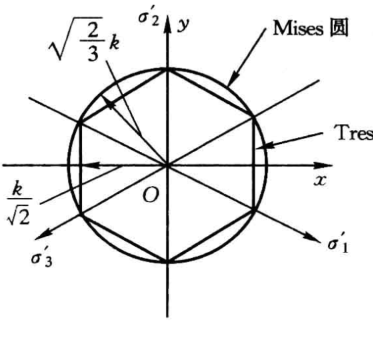
例 平衡方程的弱形式
三维变形体的方程
\[\frac{\partial\sigma_{xx}}{\partial x}+\frac{\partial\tau_{xy}}{\partial y}+\frac{\partial\tau_{xz}}{\partial z}+b_{x}=0\\\frac{\partial\tau_{xy}}{\partial x}+\frac{\partial\sigma_{yy}}{\partial y}+\frac{\partial\tau_{yz}}{\partial z}+b_{y}=0\\\frac{\partial\tau_{xz}}{\partial x}+\frac{\partial\tau_{yz}}{\partial y}+\frac{\partial\sigma_{zz}}{\partial z}+b_{z}=0
\]
上式也表示成简洁的形式
\[\mathbb{L}([\sigma])=\mathbb{F}([\sigma])+\{b\}=0
\]
\[\\{F}([\sigma])=[\nabla([\sigma])]^{\mathrm{T}} \\
\]
\[\\\nabla=\left[\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right]\\
\]
\[[\sigma]=
\begin{bmatrix}
\sigma_{xx}&\tau_{xy}&\tau_{xz}\\ \tau_{xy}&\sigma_{yy}&\tau_{yz}\\
\tau_{xz}&\tau_{yz}&\sigma_{zz}
\end{bmatrix}
\]
应用加权残值法
\[\int\limits_{V}\delta\{U\}^{\mathrm{T}}\{\mathbb{F}([\sigma])+\{b\}\} \mathrm{d}V=0
\]
\(V\) 是变形体的体积
\[\begin{aligned}\int_{V} & {\left[\delta u\left(\frac{\partial \sigma_{x x}}{\partial x}+\frac{\partial \tau_{x y}}{\partial y}+\frac{\partial \tau_{x z}}{\partial z}+b_{x}\right)+\delta y\left(\frac{\partial \tau_{x y}}{\partial x}+\frac{\partial \sigma_{y y}}{\partial y}+\frac{\partial \tau_{y z}}{\partial z}+b_{y}\right)\right.} \\& \left.+\delta w\left(\frac{\partial \tau_{x z}}{\partial x}+\frac{\partial \tau_{y z}}{\partial y}+\frac{\partial \sigma_{z z}}{\partial z}+b_{z}\right)\right] \mathrm{d} V\end{aligned}
\]
为了获得弱形式,采用格林公式进行分布积分,考虑第一项
\[\int\limits_{V}\delta u\frac{\partial\sigma_{xx}}{\partial x} \mathrm{d}V=\int\limits_{A}\delta u\sigma_{xx}l_{x}\mathrm{d}A-\int\limits_{V}\sigma_{xx}\frac{\partial(\delta u)}{\partial x} \mathrm{d}V
\]
重复上面的方法,对剩下部分分布积分
\[\begin{aligned}
&\int_{V}\left(\sigma_{xx}\frac{\partial(\delta u)}{\partial x}+\tau_{xy}\Big(\frac{\partial(\delta u)}{\partial y}+\frac{\partial(\delta v)}{\partial x}\Big)+\tau_{xz}\Big(\frac{\partial(\delta u)}{\partial z}+\frac{\partial(\delta w)}{\partial x}\Big)+\cdots+\sigma_{zz}\frac{\partial(\delta w)}{\partial z}\right) \\
&- \delta ub_{x}-\delta vb_{y}-\delta wb_{z}\Big)\mathbf{d}V+\int_{A}\Big(\delta u(\sigma_{xx}l_{x}+\tau_{xy}l_{y}+\tau_{xz}l_{z}) \\
&+\delta v(\tau_{xy}l_{x}+\sigma_{yy}l_{y}+\tau_{yz}l_{z})+\delta w(\tau_{xz}l_{x}+\tau_{yz}l_{y}+\sigma_{zz}l_{z})\Big)\mathrm{d}A=0
\end{aligned}
\]
其中\(\delta()\)为线性操作符,表示
\[\frac{\partial(\delta u)}{\partial x}=\frac{\delta(\partial u)}{\partial x}=\delta\frac{(\partial u)}{\partial x}=\delta\epsilon_{xx}
\]
因此位移的偏导数可以表示为
\[\delta\{\epsilon\}^\mathrm{T}=\left[\delta\frac{(\partial u)}{\partial x},\delta\frac{(\partial v)}{\partial y},\cdots,\left(\delta\frac{(\partial w)}{\partial x}+\delta\frac{(\partial u)}{\partial z}\right)\right]^\mathrm{T}
\]
积分的前9项可以表示为
\[\int\limits_{V}\delta\{\epsilon\}^{\mathrm{T}}\{\sigma\} \mathrm{d}V
\]
其余项目可以表示为
\[-\int\limits_{V}\delta\{U\}^{\mathrm{T}}\{b\} \mathrm{d}V
\]
而对于曲面的积分可以表示
\[-\int\limits_{A}\delta\{U\}^{\mathrm{T}}\{t\} \mathrm{d}A
\]
其中\({t}\)表示应力矢量,其表达式为
\[\{t\}=\begin{Bmatrix}t_x\\t_y\\t_z\end{Bmatrix}=\begin{Bmatrix}\sigma_{xx}l_x+\tau_{xy}l_y+\tau_{xz}l_z\\\tau_{xy}l_x+\sigma_{yy}l_y+\tau_{yz}l_z\\\tau_{xz}l_x+\tau_{yz}l_y+\sigma_{zz}l_z\end{Bmatrix}
\]
因此分布积分和式可以表示
\[\int\limits_{V}\delta\{\epsilon\}^{\mathrm{T}}\{\sigma\} \mathrm{d}V=\int\limits_{V}\delta\{U\}^{\mathrm{T}}\{b\} \mathrm{d}V+\int\limits_{A}\delta\{U\}^{\mathrm{T}}\{t\} \mathrm{d}A
\]
上式是虚功原理的表示,表明:如果一个变形力处于平衡状态,则外力在任意虚位移上所做的等于变形楼梯应力虚应变能。
因此,虚功原理是平衡方程的积分弱形式。
瑞利-里兹法
函数\(\Pi\)由一组函数和偏导数组成
\[\Pi=\Pi\Big(u,\frac{\partial u}{\partial x},\frac{\partial^2u}{\partial x^2},\cdots\Big)
\]
函数\(\Pi\)的一阶变分为
\[\delta\Pi=\frac{\partial\Pi}{\partial u}\delta u+\frac{\partial\Pi}{\partial\left(\frac{\partial u}{\partial x}\right)}\delta\left(\frac{\partial u}{\partial x}\right)+\cdots
\]
其中 \(\delta u\) 和 \(\delta{\left(\frac{\partial u}{\partial x}\right)}\)是\(u\) 和\(\frac{\partial u}{\partial x}\)的变分。
积分形式的函数表达式
如果采用伽辽金法求解求解6.25,用 \(\delta\overline{u}(x)\)代替$\psi $可得
\[\int_{0}^{1}\left((\bar{u}(x)+x) \delta \bar{u}(x)-\frac{\mathrm{d} \bar{u}(x)}{\mathrm{d} x} \frac{\mathrm{d} \delta \bar{u}(x)}{\mathrm{d} x}\right) \mathrm{d} x+[p \delta \bar{u}(x)]_{0}^{1}=0
\]
整理可得
\[\delta\Big[\frac{1}{2}\int\limits_{0}^{1}\overline{u}(x)^{2}\mathrm{d}x-\frac{1}{2}\int\limits_{0}^{1}\Big(\frac{\mathrm{d} \overline{u}(x)}{\mathrm{d}x}\Big)^{2}\mathrm{d}x+\int\limits_{0}^{1}x\overline{u}(x)\mathrm{d}x+\left[p\overline{u}(x)\right]_{x=1}\Big]=0
\]
上式可以简写为
\[\delta\Pi=0
\]
式中的函数\(\Pi\)的表达式为
\[\Pi=\frac{1}{2}\int\limits_{0}^{1}\overline{u}(x)^{2}\mathrm{d}x-\frac{1}{2}\int\limits_{0}^{1}\left(\frac{\mathrm{d} \overline{u}(x)}{\mathrm{d}x}\right)^{2}\mathrm{d}x+\int\limits_{0}^{1}x\overline{u}(x)\mathrm{d}x+\left[p\overline{u}(x)\right]_{x=1}
\]
可以看出,函数\(\Pi\)是函数\(\overline{u}(x)\)及其导数的函数。
瑞利-里兹法简介
如果函数是已知的,那么就可以用瑞利-里兹法(Rayleigh Ritz method)进行离散,也就是用代数方程代替微分方程。该方法需要找到诸如式(6.2)形式的满足强制边界条件的试函数,并使得上述方程取最小值,即
\[\delta\Pi=0
\]
如果用\(\{\overline{u}\}=\sum_{i=1}^n\alpha_iP_i(\{x\})\)代替 \(\overline{u}(x)\),那么6.25的变分可以表示
\[\delta\Pi=\frac{\partial\Pi}{\partial\alpha_1}\delta\alpha_1+\frac{\partial\Pi}{\partial\alpha_2}\delta\alpha_2+\cdots+\frac{\partial\Pi}{\partial\alpha_n}\delta\alpha_n=0
\]
对于任意的$\delta\alpha_{i} , \delta\Pi $必须等于零,因此
\[\begin{aligned}&\frac{\partial \Pi}{\partial \alpha_{1}}=0\\&\frac{\partial \Pi}{\partial \alpha_{2}}=0\\&\text{:}\\&\frac{\partial \Pi}{\partial \alpha_{n}}=0\end{aligned}
\]
上式包含了n个方程,可以求解n个待求的参数\(a_i\).
例1 有泛函
\[\Pi=\frac{1}{2}\int\limits_{0}^{1}\overline{u}(x)^{2} \mathrm{d}x-\frac{1}{2}\int\limits_{0}^{1}\left(\frac{\mathrm{d} \overline{u}(x)}{\mathrm{d}x}\right)^{2}\mathrm{d}x +\int\limits_{0}^{1}x\overline{u}(x) \mathrm{d}x
\]
它是下面微分方法的等效积分形式
\[\mathbb{B}(u(x))=\frac{\mathrm{d}^2u(x)}{\mathrm{d}x^2}+u(x)+x=0\quad {on}\quad \Omega=[0,1]
\]
边界条件
\[\begin{aligned}u(x&=0)=0\\u(x&=1)=0\end{aligned}
\]
该方程的解析解为
\[u(x)=\frac{\sin(x)}{\sin(1)}-x
\]
下面采用瑞利里茨法求解,假设满足边界条件的试函数为
\[\begin{aligned}&u_{1}=x(x-1)\alpha_{1}\quad\longrightarrow\text{一个参数}\\&u_{2}=x(x-1)(\alpha_{1}+\alpha_{2}x)\quad\text{两个参数}\end{aligned}
\]
将第一个试函数代入,可得
\[\begin{aligned}
\Pi _1
& =\frac{1}{2}\int\limits_{0}^{1}\left(\alpha_{1}^{2}(x^{2}-x)^{2}-\alpha_{1}^{2}(2x-1)^{2}+2\alpha_{1}x^{2}(x-1)\right)\mathrm{d}x \\
&=\frac{1}{2}\int_{0}^{1}\left(\alpha_{1}^{2}x^{4}+(\alpha_{1}-\alpha_{1}^{2})2x^{3}+(3\alpha_{1}^{2}+2\alpha_{1})x^{2}+4\alpha_{1}^{2}x-\alpha_{1}^{2}\right)\mathrm{d}x
\end{aligned}
\]
对上式进行积分
\[\Pi _1=- \frac {3}{20} \alpha_1 ^2- \frac {1}{12}\alpha_1
\]
对上式进行变分,可得
\[\delta\Pi_1=\frac{\partial\Pi_1}{\partial\alpha_1}\delta\alpha_1=0=-\frac6{20}\alpha_1-\frac1{12}
\]
从而可以解得
\[\alpha_1=\frac{-5}{18}
\]
试函数可以表示为
\[u_1(x)=\frac{-5}{18}x(x-1)
\]
将两个参数的第二试函数代入并积分
\[\Pi_2=-\frac{3}{20}\alpha_1^2-\frac{13}{210}\alpha_2-\frac{3}{20}\alpha_1\alpha_2-\frac{1}{12}\alpha_1-\frac{1}{20}\alpha_2
\]
并将 将\(\Pi_2\)对于\(\alpha_1\)和\(\alpha_2\)进行变分,可得
\[\delta\Pi_{2}=\frac{\partial\Pi_{2}}{\partial\alpha_{1}}\delta\alpha_{1}=-\frac{3}{10}\alpha_{1}-\frac{3}{20}\alpha_{2}-\frac{1}{12}=0\\\delta\Pi_{2}=\frac{\partial\Pi_{2}}{\partial\alpha_{2}}\delta\alpha_{2}=-\frac{3}{20}\alpha_{1}-\frac{13}{105}\alpha_{2}-\frac{1}{20}=0
\]
联合求解
\[\alpha_{1}=\frac{-71}{369}\\\alpha_{2}=\frac{-7}{41}
\]
因此试函数可表示为
\[u_2(x)=x(x-1)\Big(-\frac{71}{369}-\frac{7x}{41}\Big)
\]
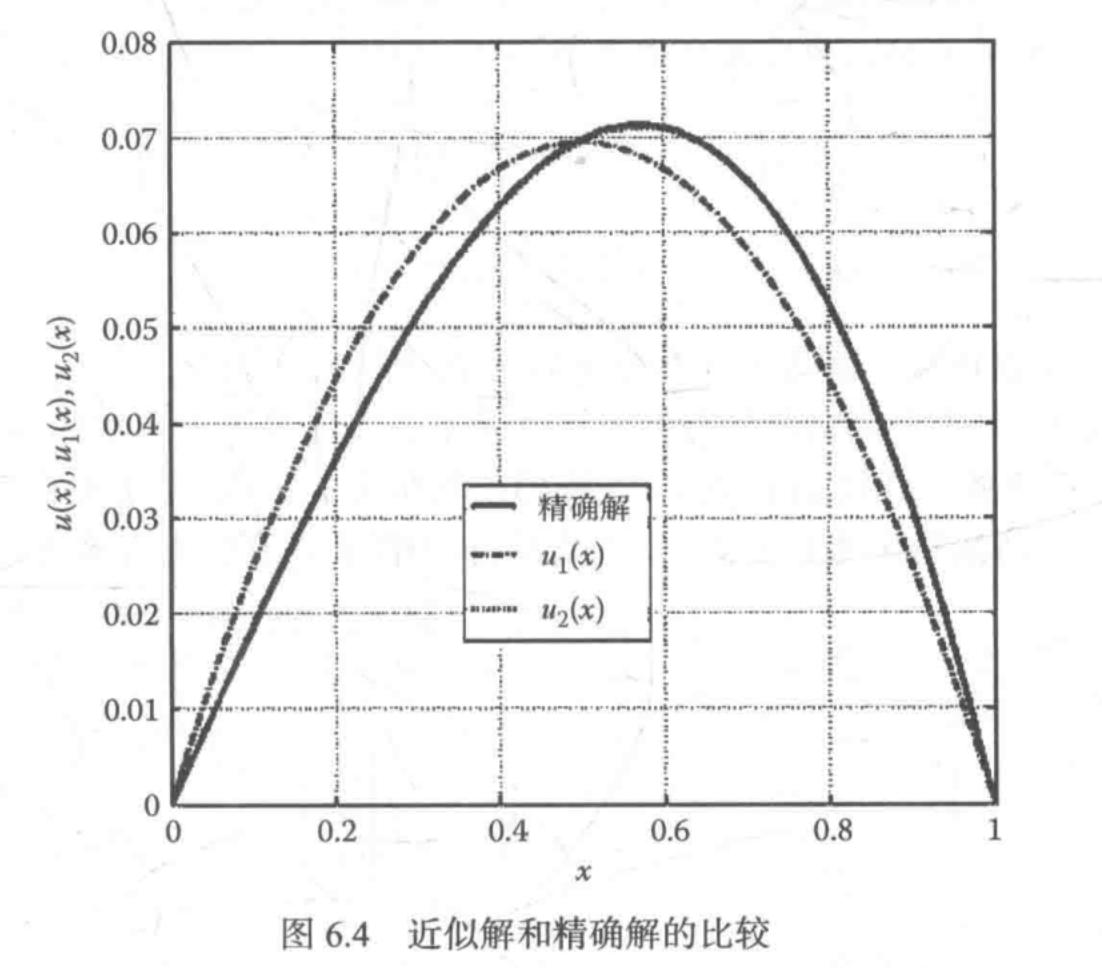
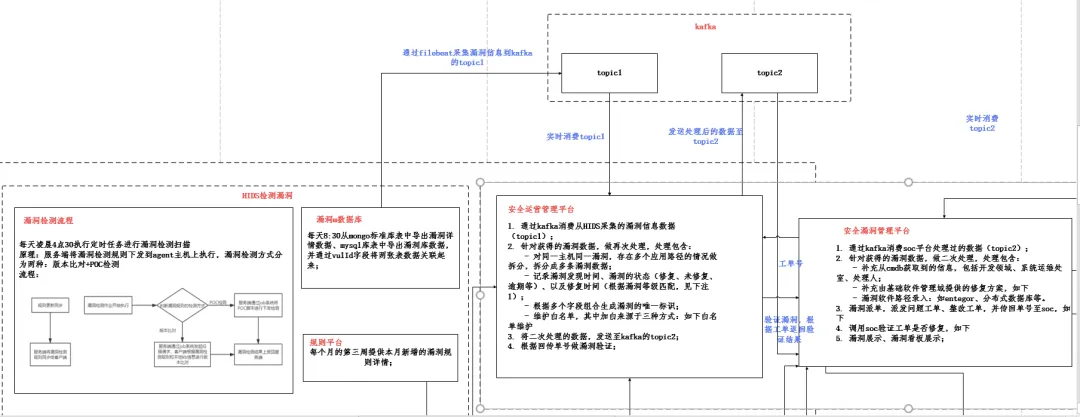
参考文献:MATLAB和Abaqus有限元分析理论与应用
附录
格林公式
设 \(\mathbf{F}(x, y)=M(x, y) \mathbf{i}+N(x, y) \mathbf{j}\) 为一个平面流体的速度场, 并设 \(M,N\)在区域 R 的每一点处的一阶偏导连续. 设 (x, y) 为 R 内一点, 且设 A 为一个小矩形, 它的一个顶点在 (x, y) , 且整个小矩形均位于 R 内 (图 13.24). 矩形的边平行于坐标轴, 长度分别为$ \Delta x $和 $ \Delta y $. 液体从底边穿出离开矩形的速率近似为
\[F( x , y ) \cdot ( - \mathbf{j})\Delta x = - N( x , y )\Delta x .
\]
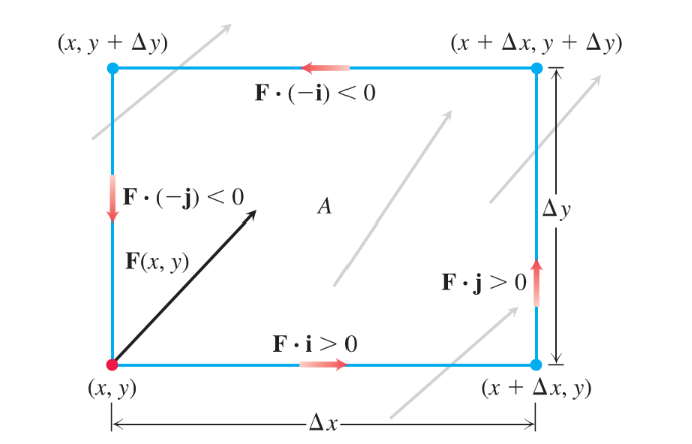
这是速度在点(x,y)的外法方向的分量乘以线段的长,比如速度以“每秒米”为单位,流出速度是以每秒乘以米,或者每秒平方米,流体沿外法线方向穿出其他三边的速度可以类似估算:
逸出速度
\[\begin{aligned}&\text{顶边}:\quad\mathbf{F}( x , y + \Delta y ) \cdot \mathbf{j}\Delta x = N( x , y + \Delta y )\Delta x\\&\text{底边}:\quad\mathbf{F}( x , y ) \cdot ( - \mathbf{j} )\Delta x = - N( x , y )\Delta x\\&\text{右边}:\quad\mathbf{F}( x + \Delta x , y ) \cdot \mathbf{i}\Delta y = M( x + \Delta x , y )\Delta y\\&\text{左边}:\quad\mathbf{F}( x , y ) \cdot ( - \mathbf{i})\Delta y = - M( x , y )\Delta y .\end{aligned}
\]
将对边加一起
\[\text{上、下边:}\quad( N( x ,y + \Delta y ) - N( x ,y ) )\Delta x \approx \left(\frac{\partial N}{\partial y}\Delta y\right)\Delta x \\\text{右、左边:}\quad(M( x + \Delta x ,y ) - M( x ,y ) )\Delta y \approx \left(\frac{\partial M}{\partial x}\Delta x\right)\Delta y .
\]
上面两式相加
\[\text{穿过矩形边界的通量} \approx \left(\frac{\partial M}{\partial x} + \frac{\partial N}{\partial y}\right)\Delta x\Delta y .
\]
两边再除以 \(\Delta x \Delta y\) 以算出单位面积的总通量或者穿过矩形的通量密度
\[\frac{\text{穿过矩形边界的通量}}{\text{矩形面积}} \approx \left(\frac{\partial M}{\partial x} + \frac{\partial N}{\partial y}\right).
\]
通量密度或散度
向量场 \(F=M\mathbf{i}+N\mathbf{j}\)\在点\((x,y)\)处的通量密度或散度为:
\[\mathrm{divF} = \frac{\partial M}{\partial x} + \frac{\partial N}{\partial y} .
\]
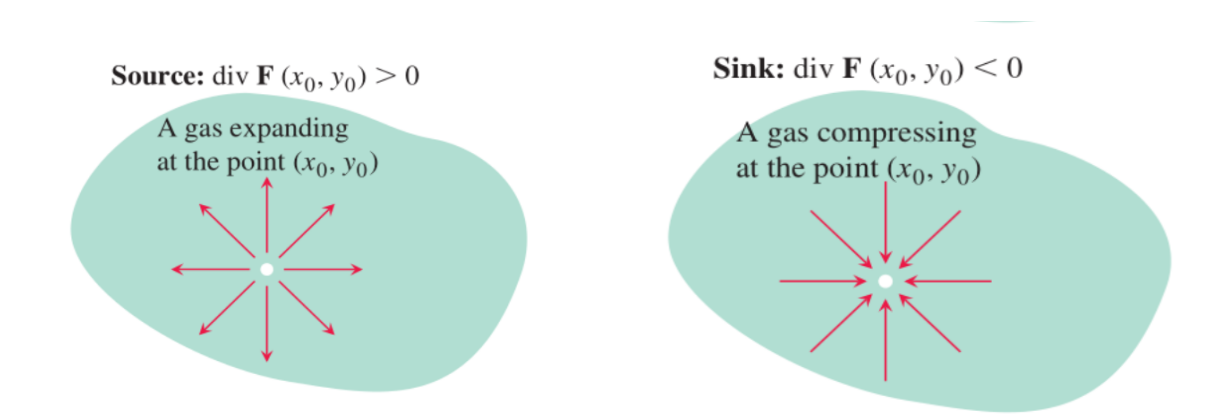
环量密度:旋度的K-分量
F绕A的边界的逆时针环量是沿着边界的流速之和,对底边,流速近似为:
\[F( x , y ) \cdot i \Delta x = M( x , y )\Delta x
\]
这是F在切向量i方向上的数值分量乘以该线段的长,而沿着其他边的逆时针的流速可以类似表示
\[\begin{aligned}
\text{上边:} \quad & \mathbf{F}( x , y + \Delta y ) \cdot ( - \mathbf{i})\Delta x = - M( x , y + \Delta y )\Delta x \\
\text{下边:} \quad & \mathbf{F}( x , y ) \cdot\mathbf{i} \Delta x = M( x , y )\Delta x \\
\text{右侧边:} \quad & \mathbf{F}( x + \Delta x ,y ) \cdot \mathbf{j} \Delta y = N( x + \Delta x ,y )\Delta y \\
\text{左侧边:} \quad & \mathbf{F}(x,y)\cdot(-\mathbf{i})\Delta\gamma = - N(x,y)\Delta\gamma .
\end{aligned}
\]
把对边的结果相加:
\[\text{上与下}:- ( M( x , y + \Delta y ) - M( x , y ) )\Delta x \approx- \left(\frac{\partial M}{\partial y}\Delta y\right)\Delta x\\\text{右与左}:\quad( N( x + \Delta x , y ) - N( x , y ) )\Delta y \approx \left(\frac{\partial N}{\partial x}\Delta x\right)\Delta y .
\]
两式相加,除以 \(\Delta x \Delta y\)
\[\frac{\text{绕矩形的环量}}{\text{矩形面积}} \approx \left(\frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}\right).
\]
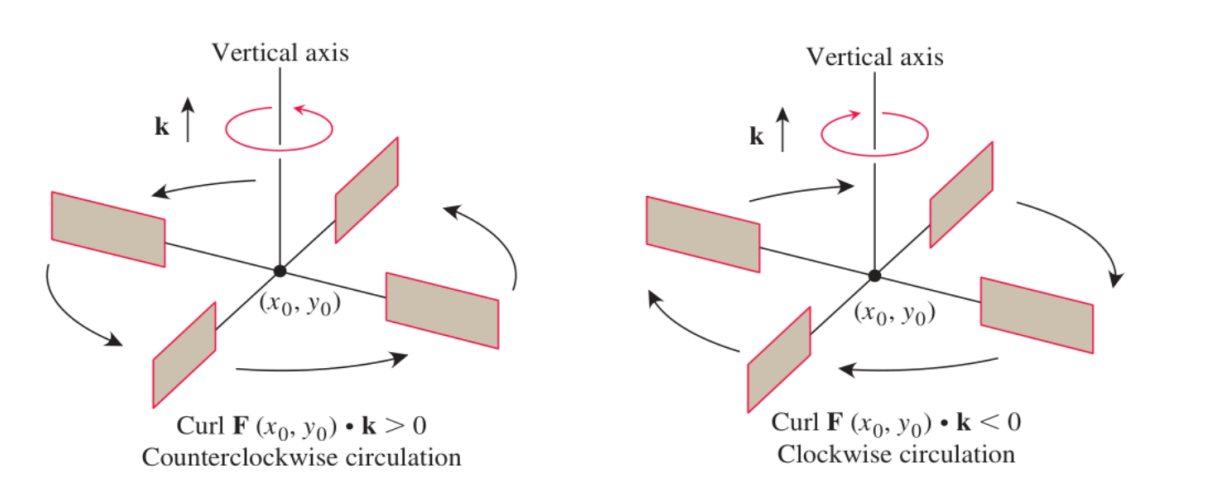
环量密度或旋度的k-分量
向量场$ F= Mi+Nj$在 \((x,y)\)的环量密度或者旋转的k-分量是数量值
\[(\mathrm{curl~}\mathbf{F})\cdot\mathbf{k} = \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}.
\]
格林定理的两种形式
格林定理的一种形式:在合适的条件下,穿过平面内一简单的闭曲线的向量场向外的通量等于该等于该曲线所围区域谁给你的散度的二重积分。
Green定理(通量-散度形式或法向形式)
场\(F=Mi+Nj\)穿过一简单闭合曲线C向外的通量等于 div F在C 所围区域R上的二重积分
\[\oint\limits_{c}\mathbf{F}\cdot\mathbf{n}\:\mathrm{d}s\:=\:\oint\limits_{c}M\mathrm{d}y\:-\:N\mathrm{d}x\:=\:\iint\limits_{R}\left(\frac{\partial M}{\partial x}\:+\:\frac{\partial N}{\partial y}\right)\mathrm{d}x\mathrm{d}y \\向外通量 \qquad \qquad \qquad\qquad 散度积分
\]
格林定理的一种形式:向量场绕一简单的闭曲线逆时针的环流量等于场在该曲线缩在区域的旋度k分量的二重积分。
Green定理(环量-旋度形式或切向形式)
场\(F=Mi+Nj\)绕平面简单闭曲线C的逆时针方向的环量等于(curl F)k 在在C 所围区域R上的二重积分
\[\oint_{c}\mathbf{F}\cdot\mathbf{T}\mathrm{d}s\:=\:\oint_{c}M\mathrm{d}x\:+\:N\mathrm{d}y\:=\:\iint_{R}\left(\frac{\partial M}{\partial x}\:-\:\frac{\partial N}{\partial y}\right)\mathrm{d}x\:\mathrm{d}y\\
逆时针方向的环量 \qquad\qquad\qquad\qquad 旋度积分
\]
格林定理的两种形式是等价的
用格林公式证明线积分
如何把一些不同的曲线首尾相连地构成一条闭曲线C,那么在C上计算的积分过程会冗长、繁琐,因为有那么不同的积分要一个个计算。若C界出一个区域R,又在该区域可应用格林定理,那么,就能用格林定理把环绕C的线积分转成成R上的二重积分。
例1 (用格林公式证明线积分)计算线积分\(\oint_{c}xy\operatorname{d}y - y^{2}\operatorname{d}x\),其中C为正方形,是由直线x=1,y=1从第一象限截出的部分
这里用格林公式的两种形式各做一次,将正方向的线积分变成以正方形为边界的区域的二重积分。
- 用法向形式的公式
\[\begin{aligned}
\oint_{c}xy\operatorname{d}y - y^{2}\operatorname{d}x& =\iint_{k}\left( y + 2 y \right)\mathrm{d}x\mathrm{d}y = \int_{0}^{1}\int_{0}^{1}3 y \mathrm{d}x \mathrm{d}y \\
&=\int_{0}^{1}\bigl[ 3 xy \bigr]_{ x = 0}^{ \lambda = 1}\mathrm{d} y = \int_{0}^{1}3 y \mathrm{d} y = \left.\frac{3}{2} y^{2} \right|_{0}^{1} = \frac{3}{2} ,
\end{aligned}
\]
2.用切向形式的公式
\[\oint_{c} - y^{2}\mathrm{d}x + xy \mathrm{d}y = \iint_{R} ( y - ( - 2y ) ) \mathrm{d}x \mathrm{d}y = \frac{3}{2} .
\]
对特殊区域格林定理的证明
设C为xy平面内的一条光滑简单闭曲线,具有性质:平行坐标轴的直线与C至多交于两点,设R为C所围的区域,并设M,N及他们的一阶偏导数在某个包含C和R的开区域的每一个点上都连续,以下证明格林定理的环量-旋度形式
\[\:\oint_{c}M\mathrm{d}x\:+\:N\mathrm{d}y\:=\:\iint_{R}\left(\frac{\partial M}{\partial x}\:-\:\frac{\partial N}{\partial y}\right)\mathrm{d}x\:\mathrm{d}y\\
\]
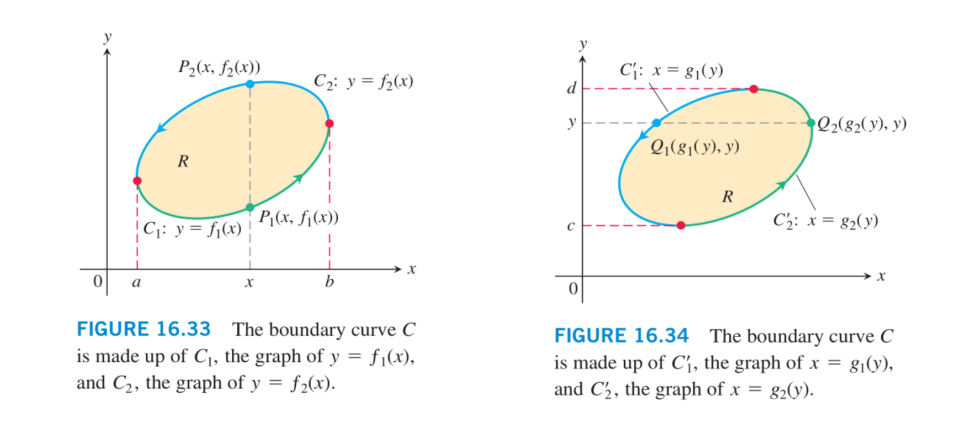
如图所示,C由两段标明方向的部分组成:
\[\begin{array}{rcl}C_1 : y&= f_1( x ) , a \leqslant x \leqslant b ,\\C_2 : y&= f_2( x ) , b \geqslant x \geqslant a .\end{array}
\]
对任何a,b间的x,我们能关于y从$ y= f_1( x ) $ 到$ y= f_2( x ) \(的积分\) \frac {\partial M }{\partial y}$,得到
\[\begin{aligned}\int_{f_{1}(x)}^{f_{2}(x)}\frac{\partial M}{\partial y}\mathrm{d}y&=M( x ,y ) \bigg|_{y=f_{1}( x )} ^ {y=f_{2}( x )} \\&=M( x ,f_{2}( x ) ) - M( x ,f_{1}( x ) ) .\end{aligned}
\]
在对结果关于x从a积到b:
\[\begin{aligned}
\int_{a}^{b}\int_{f_{1}(x)}^{f_{2}(x)}\frac{\partial M}{\partial y}\mathrm{d}y\mathrm{d}x& =\int_{a}^{b}\left[ M( x ,f_{2}( x ) ) - M( x ,f_{1}( x ) ) \right]\mathrm{d}x \\
&=-\int_{b}^{a} M( x ,f_{2}( x ) ) \mathrm{d}x -\int_{a}^{b} M( x ,f_{1}( x ) ) \mathrm{d}x \\
&=-\int_{C_{2}}M\mathrm{d}x -\int_{C_{1}}M\mathrm{d}x =- \oint_{C}M\mathrm{d}x .
\end{aligned}
\]
因此
\[\oint_{c}M\mathrm{d}x = \iint_{R}\left(-\frac{\partial M}{\partial y}\right)\mathrm{d}x\mathrm{d}y .
\]
同理:
\[\oint\limits_{c}N\mathrm{d}y = \iint\limits_{R} \frac{\partial N}{\partial x}\mathrm{d}x\mathrm{d}y .
\]
曲面面积和曲面积分
小切平面 \(\Delta P_k\)分割近似所有小曲面 \(\Delta\sigma_{k}\),把他们合在一起构成曲面,因此
\[\sum\Delta P_k = \sum \frac{\Delta A_k}{|\cos \gamma_k|}
\]
上式是以下二重积分的近似
\[\iint_R\frac1{\mid\cos\gamma\mid}\mathrm{d}A .
\]
曲面面积公式
定义在一个有界闭平面区域R上的曲面
\[\text{曲面面积 }=\iint_R\frac{|\nabla f|}{|\nabla f\cdot\mathbf{p}|}\mathrm{d}A ,
\]
其中p是R的单位法向量,且$ \Delta f \cdot≠ p $
于是面积就是向量$ \Delta f$ 的模(长度)除以$ \Delta f$在R的法向的数值分量的绝对值的二重积分。
曲面积分求通量
参考文献: 托马斯微积分13版