QOJ 7185
题目描述
有 \(n\) 个学生和 \(k\) 门科目,第 \(i\) 个学生选择第 \(k\) 门科目的消耗为 \(a_{i,j}\) 。第 \(i\) 门科目至多被 \(b_i\) 个学生选择。希望求出每一个学生选择恰好一门科目的最小消耗和。
\(n \leq 5\times 10^4 ,k \leq 10\) 。
思路点拨
看到这个题目很容易想到一个网络流建模:
-
一个源点,一个汇点,\(n\) 个代表学生的节点,\(k\) 个代表科目的节点。
-
学生节点向源点连流量为 \(1\) ,代价为 \(0\) 的边。
-
科目节点向汇点连流量为 \(b_i\) ,代价为 \(0\) 的边。
-
第 \(i\) 个同学向第 \(j\) 个科目练流量为 \(1\) ,代价为 \(a_{i,j}\) 的边。
最终该网络的最小费用最大流就是正确答案。相比之下我们更加关心图的性质以及增广路的形态。
经过观察,图具有如下性质:
-
图是一张二分图,那么每一条增广路除了源点和汇点之外都是左-右-左交替的。
-
最短路本身的性质:不会经过相同的节点(该网络图不存在负环)。
-
关键性质:注意到结合上述两个性质,每一条增广路的长度都是 \(O(k)\) 级别的,因为右部点的数量很少。
我们将一次增广路径画出来:
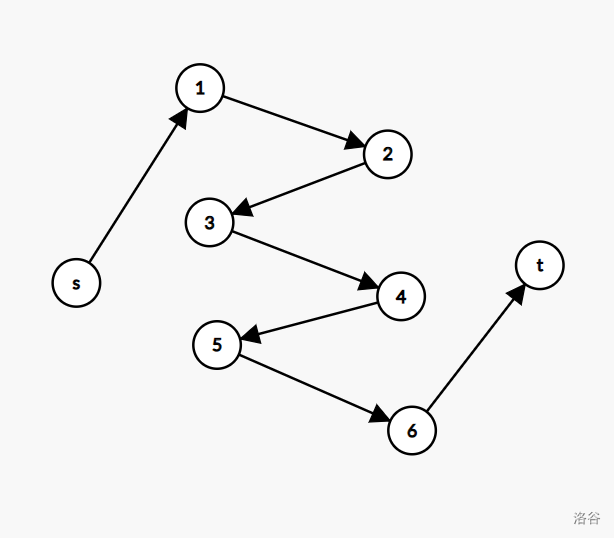
这条增广路有什么具体含义吗?\(2\) 科目有向 \(3\) 学生有流量的边,就意味着 \(2\) 学生选择了 \(3\) 科目。同理, \(5\) 学生选择了 \(6\) 科目。而 \(1\) 学生有向 \(2\) 科目有流量的边,就意味着 \(1\) 学生在此之前没有选择 \(2\) 科目,现在去选择 \(2\) 科目。同理, \(3\) 学生选择 \(4\) 科目,\(5\) 学生选择 \(6\) 科目。
那么我们考虑将路径分为几个部分:
- 从源点到达第一个左部点,从左部点到达第一个右部点。
- 对于一个右部点,认为一次移动是"右-左-右"。
- 右部点经过若干次移动到达最后一个右部点,并走向汇点。
当然,这个路径的权值和需要尽可能的小。
先考虑如何维护出两个右部点 \((i,j)\) 之间的移动 \(i \rightarrow x \rightarrow j\) ,其中 \(x\) 是一个左部节点,需要 \(a_{x,j}-a_{x,i}\) 尽量小才可以。在此移动中,一定有 \(x\) 选择了 \(i\) 科目。不妨对于每一个 \(i,j\) 维护一个堆,堆中保存了选择 \(i\) 科目的全部节点,权值就是 \(a_{x,j}-a_{x,i}\) ,取堆顶就可以了。
那么对于上述路径中的 \(2,3\) 部分,就可以对于右部点建立一张新图:两个节点 \((i,j)\) 之间的权值就是对应堆的堆顶。每一个节点还连向了一个汇点。对此图进行 SPFA ,求出 \(dis_i\) 表示从 \(i\) 科目出发,到达汇点的一个最小费用。
接下来考虑维护第一部分。我们可以枚举第一个右部点 \(j\),去找到最优的,可以到达它的左部点 \(i\)。这个左部点一定满足没有选择这个右部点 ,不妨对于每一个右部点,维护没有选择它的左部点集合,每一次取出 \(a_{i,j}\) 最小的 \(i\) 即可,可以使用一个堆维护。
我们还存在一个问题,就是增广一条路径之后需要做出一些修改操作。具体而言就是部分节点( \(O(k)\) 级别)会更改选择的科目,但是上述我们只是维护了一些堆,换成可删堆就行。
单轮增广的时间复杂度是 \(O(k^3+k^2\log n)\) 。这里 \(O(k^3)\) 来自我们建立新图后的SPFA,\(O(k^2 \log n)\) 是因为我们增广路中有 \(O(k)\) 个左部点,会影响到 \(O(k)\) 个右部点。一个左部点每影响一个右部点 \(i\),就会对于每一个右部点 \(j\) 修改 \((i,j)\) 的移动所对应的堆,这造成 \(O(k^2)\) 次堆删除操作。
一共增广 \(n\) 轮,时间复杂度 \(O(n(k^3+k^2\log n))\) 。
[AGC018C] Coins
题目描述
有 \(x+y+z\) 个人,第 \(i\) 个人有 \(A_i\) 个金币,\(B_i\) 个银币,\(C_i\) 个铜币。
要选出 \(x\) 个人获得其金币,选出 \(y\) 个人获得其银币,选出 \(z\) 个人获得其铜币。在不重复选某个人的情况下,最大化获得的币的总数。
\(x+y+z\le 10 ^ 5\)
思路点拨
这个题目可以使用上述模型解决。
对于三个硬币,可以看作上述题目的三个科目。则第 \(i\) 个人向三个硬币连流量为 \(1\) ,代价分别为 \(A_i,B_i,C_i\) 的边。
三个硬币向汇点连流量分别为 \(x,y,z\) ,代价为 \(0\) 的边。求出最大费用最大流即可。
因为本题 \(k=3\) ,所以常数可以忽略。设 \(n=x+y+z\) ,时间复杂度为 \(O(n \log n)\) 。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e5+5,inf=1e18;
int A,B,C,n;
int a[MAXN][4];
struct heap{priority_queue<pair<int,int>> q1,q2;void push(pair<int,int> x){q1.push(x);}void pop(pair<int,int> x){q2.push(x);}pair<int,int> top(){while(!q2.empty()&&q1.top()==q2.top())q1.pop(),q2.pop();if(q1.empty()) return make_pair(-inf,0);return q1.top();}
}q[4][4],p[4];int e[5][5],dis[5],pre[5];
bool vis[5];
void SPFA(){queue<int> q;for(int i=1;i<=4;i++)dis[i]=-inf,pre[i]=0;dis[4]=0;q.push(4);while(!q.empty()){int u=q.front();q.pop();vis[u]=0;for(int i=1;i<=4;i++){if(dis[i]<dis[u]+e[i][u]){dis[i]=dis[u]+e[i][u];pre[i]=u;if(!vis[i]){vis[i]=1;q.push(i);}}} }
}
signed main(){cin>>A>>B>>C;n=A+B+C;for(int i=1;i<=n;i++)for(int j=1;j<=3;j++) cin>>a[i][j];int ans=0;for(int i=1;i<=n;i++)for(int j=1;j<=3;j++) p[j].push(make_pair(a[i][j],i));for(int i=1;i<=n;i++){for(int i=1;i<=3;i++){e[4][i]=e[i][4]=-inf;for(int j=1;j<=3;j++)e[i][j]=q[i][j].top().first;}if(A) e[1][4]=0;if(B) e[2][4]=0;if(C) e[3][4]=0;SPFA();int mx=-inf,id=0;for(int i=1;i<=3;i++)if(p[i].top().first+dis[i]>mx)mx=p[i].top().first+dis[i],id=i;ans+=mx;int pos=id;while(pre[pos]!=4){int u=pos,v=pre[pos];int x=q[u][v].top().second;for(int i=1;i<=3;i++){q[u][i].pop(make_pair(a[x][i]-a[x][u],x));q[v][i].push(make_pair(a[x][i]-a[x][v],x));}pos=pre[pos];}if(pos==1) A--;if(pos==2) B--;if(pos==3) C--;pos=p[id].top().second;for(int i=1;i<=3;i++)p[i].pop(make_pair(a[pos][i],pos));for(int i=1;i<=3;i++)q[id][i].push(make_pair(a[pos][i]-a[pos][id],pos));}cout<<ans;return 0;
}