公式
先来看看几个常见公式。
\(H_n=\frac{{\binom{2n}{n}}}{n+1}(n \ge2,n\in \mathbb{N}^*)\)
\(H_n=\frac{H_{n-1}(4n-2)}{n+1}\)
\(H_n=\sum_{i=0}^{n} H_{i}H_{n-i-1}\)
\(H_n=\binom{2n}{n}-\binom{2n}{n-1}\)
不难看出,\(\text{Catalan}\) 数列增长的很快,实际应用中不要忘记开 long long 以及及时取模。
应用
再来列几个典例。
1. 最经典的
感觉这个问题是比较本质的一个卡特兰数问题。
在 \(n\times n\) 的网格上,从 \((0,0)\) 走到 \((n,n)\),也就是左下角走到右上角,每步可以向上走一格,或者向右走一格,在任意一个时刻,你往右走的次数都不能少于往上走的次数,问你有多少种不同的合法路径。
首先总的路径数可以考虑什么时候向上走,一共有 \(\binom{2n}{n}\) 条,我们可以考虑去找不合法的路径数量。将不合法的路径画出来,不难发现一定会过 \(y=x+1\) 这条直线。我们把第一个交点到 \((n,n)\) 的路径都沿这条直线对称过去,点 \((n,n)\) 就变成了 \((n-1,n+1)\),与第一个交点前面构成了 \((0,0)\) 到 \((n-1,n+1)\) 的一条路径。
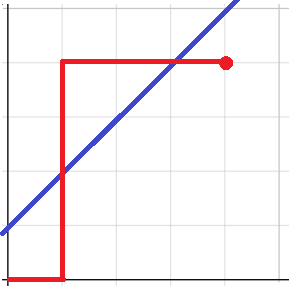
因为所有不合法的路径必然都会和 \(y=x+1\) 这条直线产生交点,所以所有的不合法路径都可以通过对称得到一条 \((0,0)\) 到 \((n-1,n+1)\) 的路径。不难发现这个条件是充要的,因为 \((0,0)\) 到 \((n-1,n+1)\) 的路径也会与直线产生交点。所以不合法路径的条数就是到 \((n-1,n+1)\) 的路径条数 \(\binom{2n}{n-1}\)。
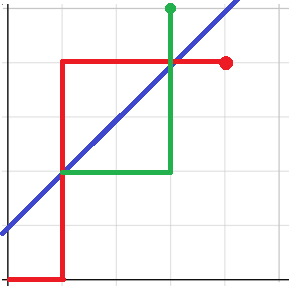
那么合法的路径总数为 \(\binom{2n}{n}-\binom{2n}{n-1}\),就是第 \(n\) 个卡特兰数。
将这个问题扩展一下,如果网格是 \(n\times m\) 的怎么做。
这个方法的本质是就是找到不合法路径唯一对应的到另一个点的路径,把 \(y=x+1\) 上下移动一下就可以了,只不过和卡特兰数关系就不大了,这个思想好像还挺重要的。
2. 01序列
你现在有 \(n\) 个\(0\) 和 \(n\) 个 \(1\),问有多少个长度为 \(2n\) 的序列,使得序列的任意一个前缀中 \(1\) 的个数都大于等于 \(0\) 的个数。
可以理解成上个问题的代数版本,可以转化成上一个问题做,也可以用代数方法来做。
首先总方案数一共有 \(\binom{2n}{n}\) 种。
然后对于任意一个不合法的数列,我们一定可以找到一个奇数位 \(2k+1\) 使得 \(1\sim 2k+1\) 有 \(k+1\) 个 \(0\),但只有一个 \(k\) 个 1。此时 \(2k+2\sim 2n\) 有 \(n-k-1\) 个 \(0\),\(n-k\) 个 \(1\)。
我们令 \(2k+2\sim 2n\) 的所有 \(0\) 变成 \(1\),\(1\) 变成 \(0\),统计一下 \(1\sim 2n\) 发现一共有 \((k+1)+(n-k)=n+1\) 个 \(0\) 与 \(k+(n-k-1)=n-1\) 个 \(1\)。
不难发现,这个东西也是充要的,所以不合法的数列的个数就是有 \(n+1\) 个 \(0\),\(n-1\) 个 \(1\) 的数列个数,也就是 \(\binom{2n}{n-1}\),方案数就是 \(\binom{2n}{n}-\binom{2n}{n-1}\)。
答案就是第 \(n\) 个卡特兰数。
当 \(n\) 个 \(1\) 和 \(m\) 个 \(0\) 的时候呢。同理推一下,答案就是 \(\binom{n+m}{m}-\binom{n+m}{m-1}\).
3. 出栈序列
一个栈的进栈序列为 \(1,2,3,\dots,n\),有多少个不同的出栈序列?
可以转化为上面这个题,但还可以用一种与栈相关的方法来做。
设 \(f(x)\) 表示 \(1\sim x\) 出栈序列个数。我们考虑当 \(k\) 出栈可以恰好把栈出空时,那么 \(1\sim k-1\) 有 \(k-1\) 个数,那么出栈序列个数就有 \(f(k-1)\) 种;\(k+1\sim n\) 有 \(n-k\) 个数,那么出栈序列个数就有 \(f(n-k)\) 种。对于 \(k\) 来说,两边的方案是独立的,于是根据乘法原理一共有 \(f(k-1)f(n-k)\) 种。
又 \(1\sim n\) 的每个数都可以将栈出空,所以 \(f(n)=f(0)f(n-1)+f(1)f(n-2)+\dots +f(n-1)f(0)=\sum_{i=0}^{n} f_{i}f_{n-i}\),你会发现这不是我们卡特兰数吗,这样你就得到了卡特兰数的递推公式。
答案就是第 \(n\) 个卡特兰数。
4. 这叫啥啊,买票问题吗
有 \(2n\) 个人排成一行进入剧场。入场费 \(5\) 元。其中只有 \(n\) 个人有一张 \(5\) 元钞票,另外 \(n\) 人只有 \(10\) 元钞票,剧院无其它钞票,问有多少种方法使得只要有 \(10\) 元的人买票,售票处就有 \(5\) 元的钞票找零?
答案就是第 \(n\) 个卡特兰数。
5. 括号序列
n对括号有多少种匹配方式?
可以理解成栈或者 01 序列,答案就是第 \(n\) 个卡特兰数。
6. 连乘
\(P=a_1×a_2×a_3×\dots×a_n\),依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?
可以理解成括号序列,答案就是第 \(n\) 个卡特兰数。
7. 二叉树计数
\(n\) 个结点可构造多少个不同的二叉树?
不难得到像栈问题那样的递归式,答案就是第 \(n\) 个卡特兰数。
8. 凸多边形划分
对角线不相交的情况下,将一个凸多边形区域分成三角形区域的方法数?
9. 圆上线段
在圆上选择 \(2n\) 个点,将这些点成对连接起来使得所得到的 $n4 条线段不相交的方法数?
例题
1. [SCOI2010] 生成字符串
仿照上面那些题推一下就行了,首先总方案数一共有 \(\binom{2n}{n}\) 种,然后对于任意一个不合法的数列,我们一定可以找到一个奇数位 \(2k+1\) 使得 \(1\sim 2k+1\) 有 \(k+1\) 个 \(0\),但只有一个 \(k\) 个 \(1\)。此时 \(2k+2\sim n+m\) 有 \(m-k-1\) 个 \(0\),\(n-k\) 个 \(1\)。我们令 \(2k+2\sim n+m\) 的所有 \(0\) 变成 \(1\),\(1\) 变成 \(0\),统计一下 \(1\sim n+m\) 发现一共有 \(n+1\) 个 \(0\) 与 \(m-1\) 个 \(1\)。于是答案就是 \(\binom{n+m}{m}-\binom{n+m}{m-1}\).
2. [HNOI2009] 有趣的数列
题意转化一下就是