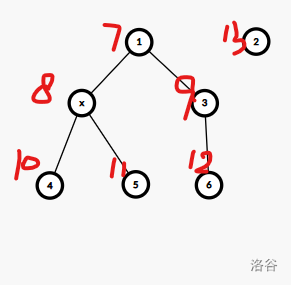
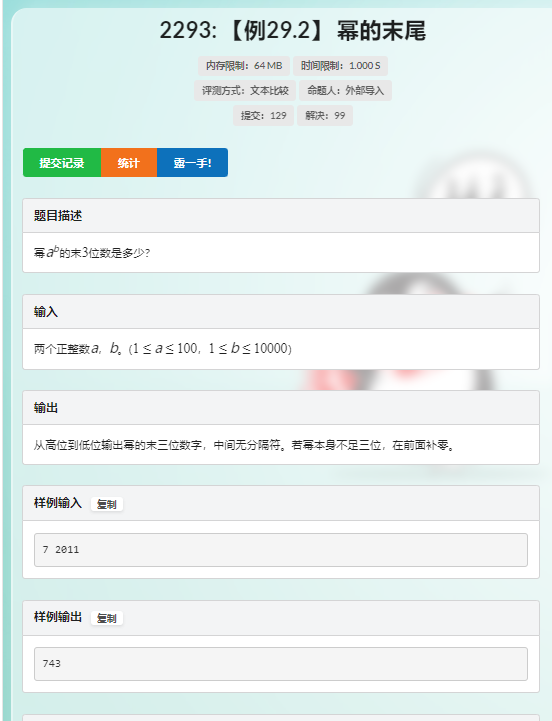
好题好题,太棒了这题!
直接想是十分困难的,你连 \(dp\) 状态都想不出合理的,因此考虑二分答案,转化成一个判定问题。下文 \(d\) 表示二分出的答案。
设 \(sum_i\) 表示 \(i\) 子树内的合法路径数,那他就一共分为两部分:
- 来自于 \(sum_{son}\),直接累加即可。
- 经过 \(i\) 的路径。
我们用一个 \(multiset\) 来存储每个儿子的 \(multiset\) 中还没有被配对的点中,距离子树根 最远的点。对于到 \(i\) 合法的路径,直接 \(sum_i++\) 即可;对于其他,从小到大进行配对,最后剩下的点中取最大值,再传递到子树根的父亲即可。
正确性显然,时间复杂度 \(O(n\log^2n)\)。
#include<bits/stdc++.h>
#define par pair<int,int>
#define int long long
using namespace std;
const int N=5e4+5;
int n,m,sum[N];
vector<par>g[N];
multiset<int>s[N];
int dfs(int x,int fa,int d){s[x].clear(),sum[x]=0;for(auto c:g[x]){int y=c.first;int z=c.second;if(y==fa) continue;int a=dfs(y,x,d)+z;sum[x]+=sum[y];if(a>=d) sum[x]++;else s[x].insert(a);}int mx=0;while(s[x].size()){int c=(*s[x].begin());if(s[x].size()==1)return max(mx,c);auto y=s[x].lower_bound(d-c);if(y==s[x].begin()) y++;if(y==s[x].end()) mx=max(mx,c);else s[x].erase(y),sum[x]++;s[x].erase(s[x].begin());}return mx;
}int check(int x){dfs(1,0,x);return (sum[1]>=m);
}signed main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);cin>>n>>m;for(int i=1,a,b,l;i<n;i++){cin>>a>>b>>l;g[a].push_back({b,l});g[b].push_back({a,l});}int l=0,r=5e8,ans;while(l<=r){int mid=(l+r)/2;if(check(mid))l=mid+1,ans=mid;else r=mid-1;}cout<<ans;return 0;
}