Rank
真欢乐吗，
不过 mission accomplished.
A. Sakurako and Water
CF2033B *900
byd 还懂难易搭配，不过这个 b 翻译甚至不着重以下主对角线差评，被硬控半个小时，直到手模样例才发觉不对。
读懂题就很简单了，最优一定是找最长的对角线每次加，一共只有 \(2n-1\) 条线，枚举一下求出每条线上的最大值之和即可。复杂度 \(\mathcal{O(n^2)}\)。
点击查看代码
#include<bits/stdc++.h>
#define fo(x, y, z) for(int (x) = (y); (x) <= (z); (x)++)
#define fu(x, y, z) for(int (x) = (y); (x) >= (z); (x)--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define lx ll
inline lx qr()
{char ch = getchar(); lx x = 0, f = 1;for(; ch < '0' || ch > '9'; ch = getchar()) if(ch == '-') f = -1;for(; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);return x * f;
}
#undef lx
#define qr qr()
#define pii pair<int, int>
#define ppp pair<pii, pii>
#define fi first
#define se second
#define M_P(x, y) make_pair(x, y)
#define P_B(x) push_back(x)
const int Ratio = 0;
const int N = 500 + 5;
const int mod = 998244353;
int n;
int a[N][N];
namespace Wisadel
{short main(){int T = qr;while(T--){n = qr; ll ans = 0;fo(i, 1, n) fo(j, 1, n) a[i][j] = qr;fo(j, 1, n){int x = 1, y = j;int maxx = 0;while(x <=n && y <= n){if(a[x][y] < 0) maxx = max(maxx, -a[x][y]);x++, y++;}ans += maxx;}fo(i, 2, n){int x = i, y = 1;int maxx = 0;while(x <= n && y <= n){if(a[x][y] < 0) maxx = max(maxx, -a[x][y]);x++, y++;}ans += maxx;}printf("%lld\n", ans);}return Ratio;}
}
signed main(){return Wisadel::main();}
// 佳墙坂诶迦币等渔塞
B. Binomial Coefficients, Kind Of
CF2025B *1100
这位更是唐氏。翻译没写 akshiM 求得是错误的组合数差评，被硬控 20min，直到手模才发觉不对。
读懂题就很简单了，手模容易发现 akshiM 求的是：
\[ans=\begin{cases}2^k\quad n\neq k\\ 1\quad\,\, n = k \end{cases}
\]
然后写个快速幂或者预处理二的幂就做完了，前者 \(\mathcal{O(T\log k)}\) 后者 \(\mathcal{O(k)}\)，不知道哪个快。
点击查看代码
#include<bits/stdc++.h>
#define fo(x, y, z) for(int (x) = (y); (x) <= (z); (x)++)
#define fu(x, y, z) for(int (x) = (y); (x) >= (z); (x)--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define lx ll
inline lx qr()
{char ch = getchar(); lx x = 0, f = 1;for(; ch < '0' || ch > '9'; ch = getchar()) if(ch == '-') f = -1;for(; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);return x * f;
}
#undef lx
#define qr qr()
#define pii pair<int, int>
#define ppp pair<pii, pii>
#define fi first
#define se second
#define M_P(x, y) make_pair(x, y)
#define P_B(x) push_back(x)
const int Ratio = 0;
const int N = 1e6 + 5, M = 1e6;
const int mod = 1e9 + 7;
int n[N];
namespace Wisadel
{ll Wqp(ll x, int y){ll res = 1;while (y){if (y & 1)res = res * x % mod; x = x * x % mod; y >>= 1;}return res;}short main(){int T = qr;fo(i, 1, T) n[i] = qr;fo(i, 1, T){int k = qr;printf("%lld\n", Wqp(2, n[i] == k ? 0 : k));}return Ratio;}
}
signed main(){return Wisadel::main();}
// 佳墙坂诶迦币等渔塞
C. QED's Favorite Permutation
CF2030D *1700
这位更是唐氏，想了半天的可持久化并查集怎么做，愣了一大圈才回头想起来可以换角度先预处理出需要的边然后做，被硬控 1.4h。
如果某个点不在自己该在的位置上那么一定需要向本来的位置移动，即当前位置到原本位置都要有边。边读入边做，好像暴力处理就行，不过我上了线段树，相当于做区间赋值操作，由于只会赋值一次所以复杂度大概处于 \(\mathcal{O(n)}\) 到 \(\mathcal{O(n\log n)}\) 之间。
然后计数当前的边，按位置记，并记录有多少该有的边没有，翻转很简单，左右做一遍就完了，同时维护上面要记的，询问只有当所有需要的边都有的时候为 YES，否则为 NO。
时间复杂度 \(\mathcal{O(n)}\) 到 \(\mathcal{O(n\log n)}\)。
点击查看代码
#include<bits/stdc++.h>
#define fo(x, y, z) for(int (x) = (y); (x) <= (z); (x)++)
#define fu(x, y, z) for(int (x) = (y); (x) >= (z); (x)--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define lx ll
inline lx qr()
{char ch = getchar(); lx x = 0, f = 1;for(; ch < '0' || ch > '9'; ch = getchar()) if(ch == '-') f = -1;for(; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);return x * f;
}
#undef lx
#define qr qr()
#define pii pair<int, int>
#define ppp pair<pii, pii>
#define fi first
#define se second
#define M_P(x, y) make_pair(x, y)
#define P_B(x) push_back(x)
const int Ratio = 0;
const int N = 2e5 + 5;
const int mod = 1e9 + 7;
int n, m;
string s;
int a[N], e[N], ned[N];
int al[N << 2];
namespace Wisadel
{#define ls (rt << 1)#define rs (rt << 1 | 1)#define mid ((l + r) >> 1)inline void Wpushup(int rt){al[rt] = al[ls] && al[rs];}inline void Wupd(int rt, int l, int r, int x, int y){if(al[rt]) return ;if(x <= l && r <= y){al[rt] = 1;return ;}if(al[rt]) al[ls] = al[rs] = 1;if(x <= mid) Wupd(ls, l, mid, x, y);if(y > mid) Wupd(rs, mid + 1, r, x, y);Wpushup(rt);}inline int Wq(int rt, int l, int r, int x){if(al[rt]) return 1;if(l == r) return al[rt];if(x <= mid) return Wq(ls, l, mid, x);else return Wq(rs, mid + 1, r, x);}short main(){int T = qr;while(T--){n = qr, m = qr;fill(al + 1, al + 1 + (n << 2), 0);fill(e + 1, e + 1 + n, 0);fo(i, 1, n){a[i] = qr;if(a[i] > i) Wupd(1, 1, n, i, a[i] - 1);if(a[i] < i - 1) Wupd(1, 1, n, a[i], i - 1);}cin >> s;s = " " + s;fo(i, 1, n) if(s[i] == 'L') e[i - 1]++;else e[i]++;int lan = 0;fo(i, 1, n - 1){ned[i] = Wq(1, 1, n, i);if(e[i] < ned[i]) lan++;}fo(i, 1, m){int x = qr;if(s[x] == 'L'){e[x - 1]--;if(e[x - 1] < ned[x - 1]) lan++;if(e[x] < ned[x]) lan--;e[x]++;s[x] = 'R';}else{e[x]--;if(e[x] < ned[x]) lan++;if(e[x - 1] < ned[x - 1]) lan--;e[x - 1]++;s[x] = 'L';}puts(lan == 0 ? "YES" : "NO");}}return Ratio;}
}
signed main(){return Wisadel::main();}
// 佳墙坂诶迦币等渔塞
D. Card Game
CF2025E *2200
不算很难的 dp，赛时由于前面打炸了导致静不下心去想。
其实想出卡特兰数了，但赛时并不知道卡特兰数是卡特兰数，所以寄了。
发现除了第一种卡牌其他卡牌都是等价的，所以只用分两种卡组讨论。
几个比较显然的结论：第一种只能先手多，其他种只能后手多，且二者多的总数相等；先手的牌一定能打出去。
那么对于第一种牌的 dp 就好想了。由于先手的牌要都能打出去，所以点数我们从大到小考虑。设 \(f_{i,j}\) 为考虑到前 \(i\) 大张牌先手比后手多 \(j\) 张的分配方案数，转移方程有：
\[f_{i,j}=\begin{cases}f_{i-1,j + 1}\qquad\qquad\quad\ j=0\\f_{i-1,j-1}+f_{i-1,j+1}\quad other \end{cases}
\]
然后考虑其他种类如何求。设 \(g_{i,j}\) 表示到第 \(i\) 种牌后手共多 \(j\) 张牌，过程依然从大到小枚举牌点数，状态转移方程为：
\[g_{i,j}=\sum_{k=0}^jg_{i-1,k}\times f_{m,j-k}
\]
总答案就很显然了，\(\sum_{i=0}^m\ g_{n,i}\times f_{m,i}\)。时间复杂度 \(\mathcal{O(n^3)}\)。
点击查看代码
#include<bits/stdc++.h>
#define fo(x, y, z) for(int (x) = (y); (x) <= (z); (x)++)
#define fu(x, y, z) for(int (x) = (y); (x) >= (z); (x)--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define lx ll
inline lx qr()
{char ch = getchar(); lx x = 0, f = 1;for(; ch < '0' || ch > '9'; ch = getchar()) if(ch == '-') f = -1;for(; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);return x * f;
}
#undef lx
#define qr qr()
#define pii pair<int, int>
#define ppp pair<pii, pii>
#define fi first
#define se second
#define M_P(x, y) make_pair(x, y)
#define P_B(x) push_back(x)
const int Ratio = 0;
const int N = 500 + 5;
const int mod = 998244353;
int n, m;
ll f[N][N], g[N][N];
namespace Wisadel
{short main(){n = qr, m = qr;f[0][0] = g[1][0] = 1;fo(i, 1, m) fo(j, 0, i)if(!j) f[i][j] = f[i - 1][j + 1];else f[i][j] = (f[i - 1][j - 1] + f[i - 1][j + 1]) % mod;fo(i, 2, n) fo(j, 0, m) fo(k, 0, j)g[i][j] = (g[i][j] + g[i - 1][k] * f[m][j - k] % mod) % mod;ll ans = 0;fo(i, 0, m) ans = (ans + g[n][i] * f[m][i] % mod) % mod;printf("%lld\n", ans);return Ratio;}
}
signed main(){return Wisadel::main();}
// 佳墙坂诶迦币等渔塞
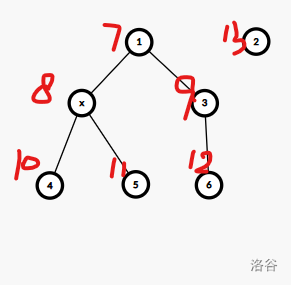
E. Long Way to be Non-decreasing
CF1967D *2800
二分答案比较好想到，可惜赛时只会暴力，还因为 \(\mathcal{O(nm)}\) 预处理导致挂 8pts。
实质上将 b 数组连完边后形成的是一个内向基环树森林。仍然沿用二分答案的思路，考虑如何 check。每个位置的值的下界即为上一个数，可以依次升序考虑直到 \(m\)，那么问题转变到求基环树上两点距离。
发现内向基环树是没办法进行 dfs 操作的，因此连边时直接反向连，然后断掉一条边就可以正常 dfs 用树上差分求解了。若两点为子树内包含关系，则直接树上差分；否则求一下环上距离即可。
时间复杂度 \(\mathcal{O(n\log n)}\)。
F. Many Games
CF2023D *2900
辅助回忆：\(T3's\ example\ is\ weaker\ than...\)
比较神奇，各种推式子证明就转化成了一个 01 背包问题。
由于出处写的很好，就不手动搬一遍了 （才不是偷懒
点击查看代码
#include<bits/stdc++.h>
#define fo(x, y, z) for(int (x) = (y); (x) <= (z); (x)++)
#define fu(x, y, z) for(int (x) = (y); (x) >= (z); (x)--)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define lx ll
inline lx qr()
{char ch = getchar(); lx x = 0, f = 1;for(; ch < '0' || ch > '9'; ch = getchar()) if(ch == '-') f = -1;for(; ch >= '0' && ch <= '9'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ 48);return x * f;
}
#undef lx
#define qr qr()
#define pii pair<int, int>
#define ppp pair<pii, pii>
#define fi first
#define se second
#define M_P(x, y) make_pair(x, y)
#define P_B(x) push_back(x)
const int Ratio = 0;
const int N = 1e6 + 5, M = 202022;
const int mod = 998244353;
int n;
double f[M], ans;
priority_queue<ll> q[100];
namespace Wisadel
{short main(){n = qr;ll sum = 0;f[0] = 1;fo(i, 1, n){int x = qr, y = qr;if(x == 100) sum += y;else q[x].push(y);}fo(i, 1, 99){fo(tim, 1, 100 / (100 - i)){if(!q[i].size()) break;int zc = q[i].top(); q[i].pop();fu(j, M, zc) f[j] = max(f[j], f[j - zc] * i / 100);}}fo(i, 0, M - 1) ans = max(ans, 1.0 * (sum + i) * f[i]);printf("%.8lf\n", ans);return Ratio;}
}
signed main(){return Wisadel::main();}
// 佳墙坂诶迦币等渔塞
末
欢乐吗？如乐。
一直犯唐 + 脑瘫错误 + 思路混乱，能赛时补出 T3 正解感觉已经尽力了。
但是回过头来看，T4 压根没往 dp 上想是个很严重的失误，不然不至于三个小时做不出来，而且 IOI 赛制确实也很考验心态，太早打部分分确实会直接禁锢住自己的思维，不打又总被不断变换的榜单干扰，这时候策略就很重要了。不过问题不大，有生之年应该打不了 IOI 赛制的正赛（
完结撒花~
待补
