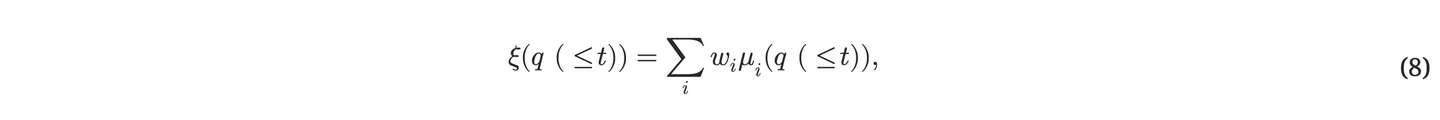「模拟赛」多校 A 层冲刺 NOIP 24

A.选取字符串

KMP、字符串好题

因为所有字符串都是大字符串的前缀，所以一旦我们每个字符串的前缀后缀的长度确定了，那么前缀后缀长什么样也就确定了

设 \(f_i\) 为所有相同前缀后缀长度可以为 \(i\) 的字符串的个数

我们枚举 \(i\in [1,n]\)，每次钦定两个串 \(p、q\) 里必须有一个是 \(S_i\)，而另一个串可以在合法的范围内任意选。

设 \(g_i\) 表示必选前缀串 \(S_i\) 时另一个串可以选的字符串的个数

那么答案就是 \(\sum_{i=1}^n \binom {f_i}{k}\times (2\times g_i-1)\) + \(\binom {n+1}{k}\)

Why：另一个串有 \(g_i\) 种可能，而 \(p、q\) 的顺序不同为不同的方案，所以乘 2，再减去 \(p、q\) 都选 \(S_i\) 的情况（这个情况 \(p、q\) 顺序不同也是一种方案）
最后 \(p、q\) 全选空串的方案单独算即为 \(n+1\) 个串里选 \(k\) 个

现在考虑 \(f_i、g_i\) 的计算：

• 对于 \(f_i\)：KMP 求出所有字符串 \(S_{[1,i]}\) 的 包的er 值 \(pi_i\)，即最长的既是前缀也是后缀的长度，那么每个字符串 \(S_i\) 相同前缀后缀可以为 \(S_{[1,\ pi_i]}\)，同时也可以为 \(S_{[1,\ pi_i]}\) 的前缀后缀，所以从大到小递推计算：f[pi[i]] += f[i];

• 对于 \(g_i\)：显然选 \(S_i\) 时同样可以为所有字符串的前缀后缀的只能是 \(S_i\) 的前缀后缀，也是同理递推得到，g[i] += g[pi[i]];

code

#include<bits/stdc++.h>
#define int long long
#define Aqrfre(x, y) freopen(#x ".in", "r", stdin),freopen(#y ".out", "w", stdout)
#define mp make_pair
#define Type int
#define qr(x) x=read()
typedef long long ll;
using namespace std;inline Type read(){char c=getchar(); Type x=0, f=1;while(!isdigit(c)) (c=='-'?f=-1:f=1), c=getchar();while(isdigit(c)) x=(x<<1)+(x<<3)+(c^48), c=getchar();return x*f;
}const int N = 1e6 + 5;
const int mod = 998244353;inline vector<int> pretix(string s){int len = s.length();vector<int>v(len+10); v[0] = 0;for(int i=1; i<len; i++){int j = v[i-1]; //v: The length of the string which from 1 to i - 1while((i == j or s[i] != s[j]) and j) j = v[j-1];if(s[i] == s[j]) j++;v[i] = j;}return v;
}string s;
int n, k, sum[N], f[N], g[N];
vector<int>pi;int fact[N], inv[N], fainv[N];
inline void AqrPre(){fact[0] = fact[1] = 1;inv[0] = inv[1] = 1;fainv[0] = fainv[1] = 1;for(int i=2; i<=n+3; i++){fact[i] = 1ll * fact[i-1] * i % mod;inv[i] = 1ll * inv[mod%i] * (mod - mod / i) % mod;fainv[i] = 1ll * fainv[i-1] * inv[i] % mod;}
}inline int C(int x, int y){return x < y ? 0 : 1ll * fact[x] * fainv[y] % mod * fainv[x-y] % mod;
}/*
思路应该是显然的？？实现也简单啊只不过我假了一版又一版那这题确实是简单签到了啊，但我打了两个半小时？？还有救么？？这让我怎么翻？后面三题只打暴力肯定不行吧
*/signed main(){ // stringAqrfre(string, string);qr(k); cin>>s; n = s.length();AqrPre(); pi = pretix(s);for(int i=0; i<n; i++) f[pi[i]]++, g[i+1] = 1;for(int i=1; i<=n; i++) g[i] += g[pi[i-1]];for(int i=n; i>=1; i--)if(i and pi[i-1]) f[pi[i-1]] += f[i];int ans = 0;for(int i=1; i<=n; i++){ans += C(f[i]+1, k) * ((g[i] + 1) * 2 - 1) % mod;ans %= mod;}cout<<(ans+C(n+1, k))%mod<<"\n";return 0;
}

B.取石子

C.均衡区间

D.禁止套娃