A.flandre
我的做法是,所有数离散化之后扔进桶里,去枚举选择 \([i,+\infty)\) 内的数的贡献,在所有的 \(i\) 里取一个最大值作为答案
lbtl 指出可能存在最优答案是选择 \([i+1,+\infty)\) 内的所有数与值为 \(i\) 的部分数的数据
和 lbtl 交涉后尝试构造一组相同元素只选后一半的数据
令 \(a_i=a_{i+1}\)
- 不选 \(i\):设为 \(s\)
- 选 \(i\):\(s+a_i+k(n-i)\)
构造一组 \(a_i+k(n-i)\lt 0,a_{i+1}+k(n-i)-k\gt 0\),即 \(a_i\lt -k(n-i),a_{i+1}-k\gt -k(n-i)\),需要使 \(a_i+k\le a_{i+1}\),即 \(a_{i+1}-a_{i}\ge k\),不符合题设 \(a_i=a_{i+1}\),无法构造出这种数据
说白了就是相等的数排完序后越靠前贡献越大,如果你选了后几个数,在这些数都是正贡献的情况下肯定要选后面的,都是负贡献的情况下肯定是为了选前面的数,否则不如不选
因此这种做法是有严格的正确性的,可能只是比较麻烦
赛时因为方案算对了答案算错了挂了 \(20\) 分,由于用方案代回去算一遍就行,因此没仔细去查错因
#include<bits/stdc++.h>
using namespace std;
template<typename T>
inline void read(T&x){x=0;char ch=getchar();int f=1;while(!isdigit(ch)){if(ch=='-') f*=-1; ch=getchar();}while(isdigit(ch)) x=x*10+ch-'0',ch=getchar();x*=f;
}
#define int long long
int n,k;
int a[1000001];
int b[1000001];
int sum[1000001];
int sumcnt[1000001];
int sumnew[1000001];
int cnt[1000001];
vector<int>pos[1000001];
signed main(){read(n);read(k);for(int i=1;i<=n;++i){read(a[i]);b[i]=a[i];}sort(b+1,b+n+1);int tmp=unique(b+1,b+n+1)-b-1;for(int i=1;i<=n;++i){a[i]=lower_bound(b+1,b+tmp+1,a[i])-b;cnt[a[i]]++;pos[a[i]].push_back(i);}for(int i=1;i<=tmp;++i){sumcnt[i]=sumcnt[i-1]+cnt[i];sum[i]=sum[i-1]+b[i]*cnt[i];sumnew[i]=sumnew[i-1]+cnt[i]*(sumcnt[i-1]);}int ans=-0x7fffffffffffffff,anscnt=1;for(int i=1;i<=tmp;++i){if(sum[tmp]-sum[i-1]+k*(sumnew[tmp]-sumnew[i]-(tmp-i)*sumcnt[i-1])>ans){ans=sum[tmp]-sum[i-1]+k*(sumnew[tmp]-sumnew[i]-(tmp-i)*sumcnt[i-1]);anscnt=i;}}if(ans<0){printf("0 0");return 0;}int tot=0,anss=0;for(int i=anscnt;i<=tmp;++i){for(int j:pos[i]){anss+=b[a[j]]+tot*k;}tot+=(int)pos[i].size();}printf("%lld %lld\n",anss,tot);for(int i=anscnt;i<=tmp;++i){for(int j:pos[i]) printf("%lld ",j);}
}
B.meirin
赛时偶遇 \(\sum\limits^{n}_{l=1}\sum\limits^{n}_{r=l}(\sum\limits_{i=l}^{r}(a_i)\times \sum\limits_{i=l}^{r}(b_i))\) 强如怪物拼尽全力无法战胜
正确的解法应该是拆贡献,考虑到你把上面这坨东西拆开一定是一个形如 \(\sum\limits^{n}_{i=1}\sum\limits_{j=1}^{n}c_{i,j}a_ib_j\) (其中 \(c_{i,j}\) 为系数) 的东西,因此考虑怎么求解这个 \(c_{i,j}\)
一种比较直观的方法是将原式改成 \(\sum\limits^{n}_{l=1}\sum\limits^{n}_{r=l}(\sum\limits_{i=l}^{r}(a_i\times \sum\limits_{i=l}^{r}(b_i)))\),这样改可以发现,只有 \(l\le i,j\le r\) 的区间 \([l,r]\) 会对 \(c_{i,j}\) 有贡献,因此 \(c_{i,j}\) 的实质就是同时包含 \(i,j\) 的区间个数
考虑求出这个玩意以后有什么用,如果你求出这东西,那么对 \([l,r]\) 区间修改 \(b_i\) 就相当于对答案增加了一个系数为 \(\sum\limits_{i=1}^{n}\sum\limits_{j=l}^{r}a_ic_{i,j}\) 的贡献,可以直接维护前缀和 \(O(1)\) 处理
剩下的工作就是降这个预处理 \(c_{i,j}\) 的复杂度了,可以考虑直接维护 \(p_i=a_i\sum\limits_{j=1}^{n}c_{i,j}=\sum\limits_{j=1}^{i-1}j(n-i+1)a_j+\sum\limits_{j=i}^{n}i(n-j+1)a_i\)(因为 \(a_i\) 不变),然后直接推一个从 \(p_{i-1}\) 到 \(p_i\) 的转移式,会发现里面有需要维护的两项 \(\sum\limits_{j=1}^{i-1}j\times a_j\) 和 \(\sum_{j=i}^{n}(n-j+1)a_j\),直接套前缀和就行
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int p=1e9+7;
int n,q;
int a[500001],b[500001];
int x[500001],y[500002],s[500001];
int qz[500001],hz[500002];
int sums[500001];
signed main(){ios::sync_with_stdio(false);cin>>n>>q;for(int i=1;i<=n;++i){cin>>a[i];}for(int i=1;i<=n;++i){cin>>b[i];}for(int i=1;i<=n;++i){qz[i]=(qz[i-1]+i*a[i]+p)%p;hz[i]=(hz[i-1]+(n-i+1)*a[i]+p)%p;} for(int i=1;i<=n;++i){x[i]=qz[i]%p;y[i]=((hz[n]-hz[i-1]+p)%p+p)%p;}int ans=0;for(int i=1;i<=n;++i){s[i]=(s[i-1]-x[i-1]+y[i]+p)%p;ans=(ans+b[i]*s[i])%p;sums[i]=(sums[i-1]+s[i])%p;}while(q--){int l,r,v;cin>>l>>r>>v;ans=((ans+(sums[r]-sums[l-1])*v%p)%p+p)%p;cout<<ans<<'\n';}
}
C.sakuya
发现期望是个诈骗东西,每两个节点相邻概率一样,题目实际上让求的是 \(\frac{\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}dist(i,j)}{m}\)
对上面这个东西不难想到,对标记节点重构一棵树,直接跑换根就能得到答案
然而这个题带修,因此需要一些智慧的处理
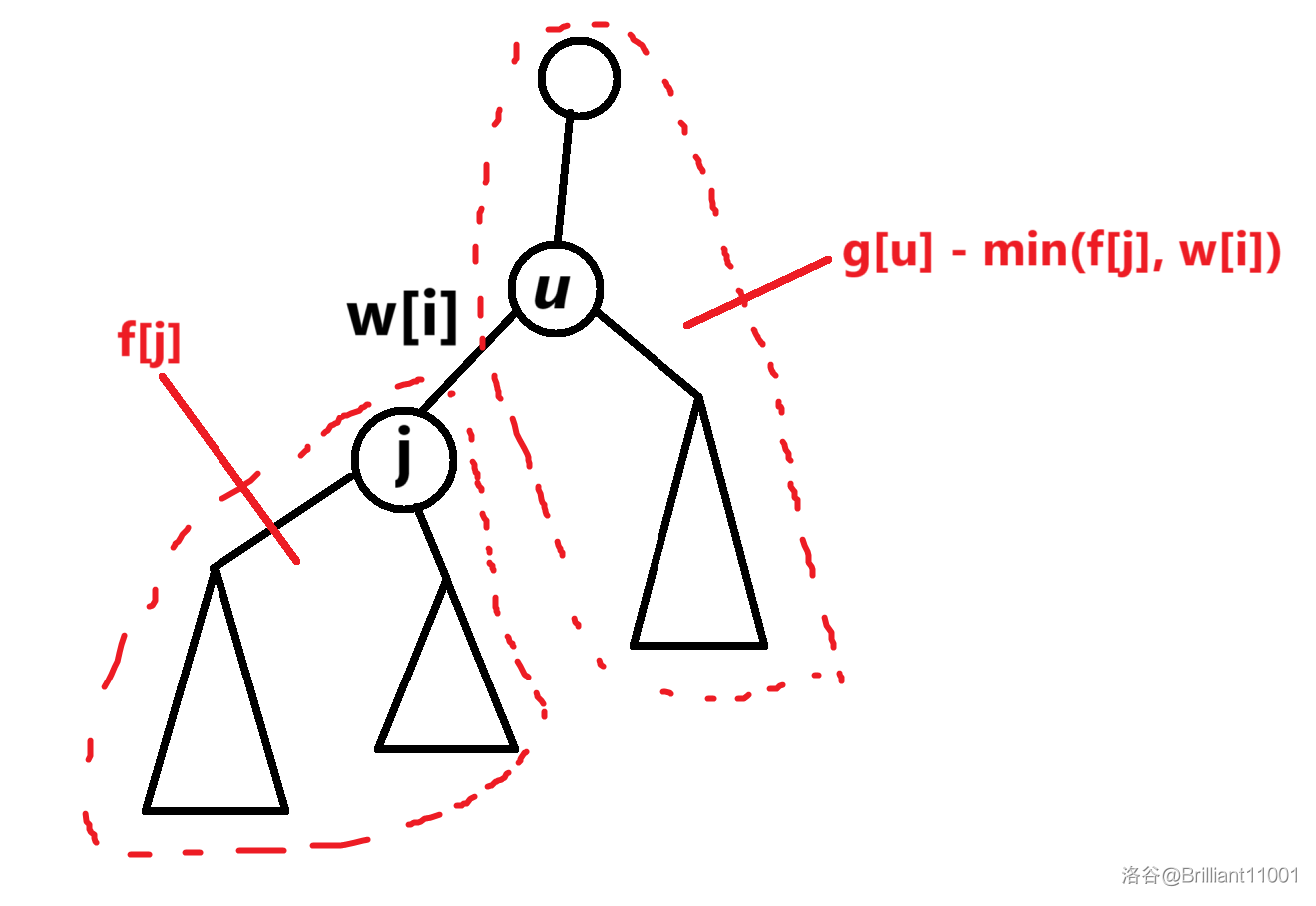
因为是单点修改,想到可以把每个边的贡献下放到两端节点处,这和上个题就一样了,设 \(c_{i,j}\) 是 \((i,j)\) 这条边的贡献系数(即在答案中出现的次数),直接对每个点统计 \(f_i=\sum\limits_{j,(i,j)\in E}c_{i,j}\) 直接就做完了,这题纯纯就是上个题的树上版本
这个 \(c_{i,j}\) 求起来更简单了,考虑这是一棵树,一条边总会将树分成两部分,那么这条边对答案的贡献就是两个部分标记节点数量的乘积
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int p=998244353;
int n,m;
struct edge{int to,w;
};
vector<edge>e[500001];
bool vis[500001];
int viscnt[500001];
int f[500001];
int fa[500001];
inline int cal(int x,int y){ //find the ans of (x,y)if(x==fa[y]) return viscnt[y]*(m-viscnt[y]);else if(y==fa[x]) return viscnt[x]*(m-viscnt[x]);assert(0);
}
void dfs1(int now,int last){if(vis[now]) viscnt[now]=1;else viscnt[now]=0;fa[now]=last;for(edge i:e[now]){if(i.to!=last){dfs1(i.to,now);viscnt[now]+=viscnt[i.to];}}
}
int ans=0;
void dfs2(int now){for(edge i:e[now]){f[now]=(f[now]+cal(i.to,now))%p;if(i.to!=fa[now]){dfs2(i.to);ans=(ans+i.w*cal(i.to,now))%p;}}
}
int power(int a,int t){int base=a,ans=1;while(t){if(t&1){ans=ans*base%p;}base=base*base%p;t>>=1;}return ans;
}
signed main(){ios::sync_with_stdio(false);cin>>n>>m;for(int i=1;i<=n-1;++i){int x,y,z;cin>>x>>y>>z;e[x].push_back({y,z});e[y].push_back({x,z});}int inv=power(m,p-2);for(int i=1;i<=m;++i){int x;cin>>x;vis[x]=true;}dfs1(1,0);dfs2(1);int q;cin>>q;while(q--){int x,k;cin>>x>>k;ans=(ans+f[x]*k%p+p)%p;cout<<ans*2*inv%p<<'\n';}
}
something
也需要迎来故事的终局了
希望一切都会好起来