T1 编辑字符串
题意
给定两个字符串,某些位置固定不动,其余相邻位置可以互换,求最大匹配长度
方案
考虑将俩串分为多段,使得每段互相匹配长度最长
将相邻可换的部分划为一段,不可交换位置的单独一段。
由下图可知,若 A 串某位置字符与 B 串两个位置字符都可以匹配,则它与一个匹配之后会拆开另一个,由此推出只要能让A串的一个位置有B处一个位置匹配,即为最优(拆散一对,合成一对不亏,交换位置要么不亏要么答案赚一)
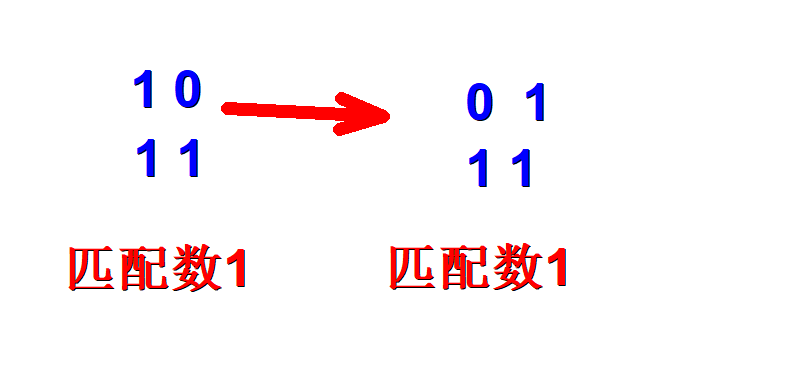
全当做字符串读入,两行之间getchar ()吞换行,再转换成数字(作为下标)
处理串:对于 A 段,若该位置固定,则自己作为一段;若位置可交换,记录可交换段的长度以及该段中 0 和 1 的个数,B 段亦是。2 * n 的时间复杂度即为 O(n)
再扫一遍 A 串,将每个位置对应段中 1 和 0 的个数分别作差取绝对值,累计扫完 A 串即为答案,时间复杂度 O(n),估分 80-100
考试结束前对拍样例
/
1
4
10000
00000
00101
01101
*/
时答案错误,紧急删了一段代码不确定是不是删错位置。
T3 树的遍历
题意
以边为基础对树遍历,并求生成多少种不同的新树。这里两棵树被认为是不同的,当且仅当至少存在某一对新的结点,它们仅在其中一棵树中连有新边。
方案
tarjan 求割边,若存在路径 u->v->w ,则删去点 v ,并建立 u->w 的新连边。时间复杂度 O(N2K),估分 20-30
乱搞树剖,每次算边时用随机数,连到哪边算哪边,极端情况下可以连接成链或者环,存在求出解的可能。赛后成功证明这样乱搞错的。
T4
题意
求区间[l, r] 内 LCA 的最大值
方案
先再各点之间连双向边,从 1 开始逐个下传等级 rank, 以形成树
a.倍增法求 LCA,采用 lg 优化
b.并查集连接点,比较每个节点 rank 大小以连接。
处理性质A:保证输入的树符合链的形态,且根结点的度数为1。预估拥有30左右理想分数,该情况下只需要正确连接成链然后求离根最近的几个点的公共LCA深度即可
赛后
博客记的
lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
考场写的
lg[i] = lg[i - 1] + (1 << lg[i - 1] == 1);
显然lca会跳错