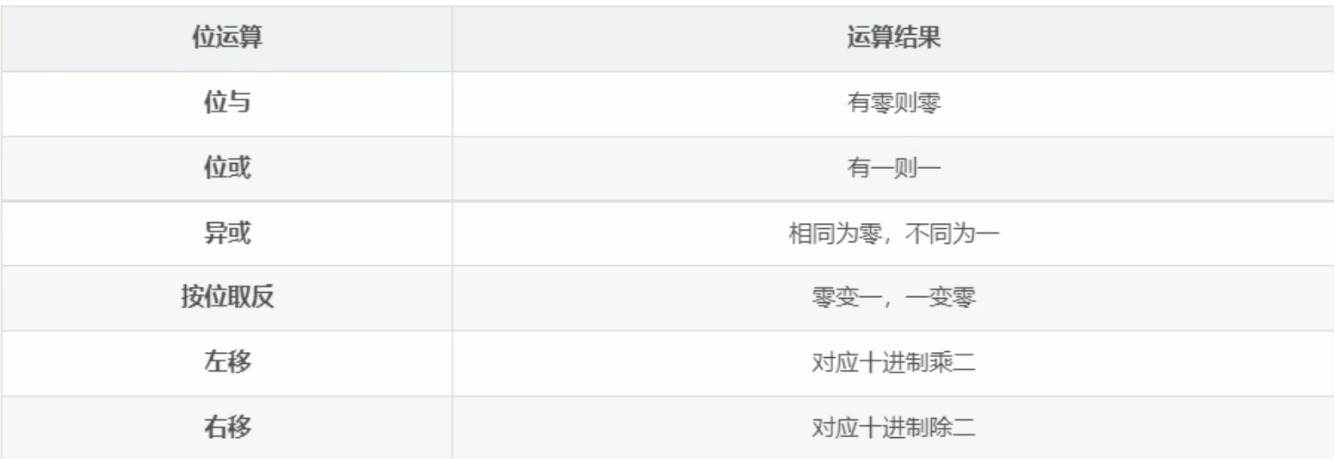
每次都试图解决问题的尽量大的一部分
如兑换硬币，先以最多数量的最大面值来迅速减少找零面值
- 首先确定基本结束条件（最直接的情况——其面值正好等于某种硬币）
- 减小问题的规模
递归算法：
#!/user/bin/env python3
# -*- coding: utf-8 -*-
def recMC(coinValueList, change):minCoins = changeif change in coinValueList:return 1else:for i in [c for c in coinValueList if c <= change]:numCoins = 1 + recMC(coinValueList, change - i)if numCoins < minCoins:minCoins = numCoinsreturn minCoinsprint(recMC([1, 5, 10, 25], 63))
[c for c in coinValueList if c <= change]是一个列表推导式。
它的作用是从coinValueList中筛选出所有小于等于change的元素。
c for c in coinValueList：这部分表示从coinValueList中取出每个元素c。
if c <= change：这是一个条件判断，只有当c小于等于change时，c才会被包含在新生成的列表中。
缺点：效率低下（原因是重复计算太多）
优化的关键在于消除重复计算，如用一个表把中间结果保存下来
这个算法的中间结果就是部分找零的最优解，在递归调用过程中已经得到的最优解被记录下来在递归调用之前，先查找表中是否已有部分找零的最优解
如果有，直接返回最优解而不是递归调用
优化：
#!/user/bin/env python3
# -*- coding: utf-8 -*-
def recDC(coinValueList, change, knownResults):minCoins = changeif change in coinValueList:knownResults[change] = 1 #记录最优解return 1elif knownResults[change] > 0:return knownResults[change] #查表成功，直接用最优解else:for i in [c for c in coinValueList if c <= change]:numCoins = 1 + recDC(coinValueList, change - i, knownResults)if numCoins < minCoins:minCoins = numCoins #找到最优解，放在列表中knownResults[change] = minCoinsreturn minCoinsprint(recDC([1, 5, 10, 25], 63, [0]*64))
如果没有，才进行递归调用
√通过记忆化/函数值缓存技术提高了递归解法的性能
动态规划解法：
动态规划算法采用了一种更有条理的方式来得到问题的解
找零兑换的动态规划算法从最简单的“1分钱找零”的最优解开始，逐步递加上去，直到我们需要的找零钱数
在找零递加的过程中，设法保持每一分钱的递加都是最优解，一直加到求解找零钱数，自然得到最优解
问题的最优解包含了更小规模子问题的最优解，这是一个最优化问题能够用动态规划策略解决的必要条件
https://www.bilibili.com/video/BV1gy4y1E7M5?t=328.5&p=53
明天再看
