leetcode2055. 蜡烛之间的盘子 - 前缀和

这道题目作为比较单纯的前缀和题目，不需要额外的一些知识，只需要了解前缀和数组的生成与使用即可，并且也有一定的难度（难度分1819），是一个比较好的前缀和例题。

题干

算术评级: 6第 64 场双周赛Q3

给你一个长桌子，桌子上盘子和蜡烛排成一列。给你一个下标从 0 开始的字符串 s ，它只包含字符 '' 和 '|' ，其中 '' 表示一个 盘子 ，'|' 表示一支 蜡烛 。

同时给你一个下标从 0 开始的二维整数数组 queries ，其中 queries[i] = [lefti, righti] 表示 子字符串 s[lefti...righti] （包含左右端点的字符）。对于每个查询，你需要找到 子字符串中 在 两支蜡烛之间 的盘子的 数目 。如果一个盘子在 子字符串中 左边和右边 都 至少有一支蜡烛，那么这个盘子满足在 两支蜡烛之间 。

比方说，s = "|||||" ，查询 [3, 8] ，表示的是子字符串 "||**|" 。子字符串中在两支蜡烛之间的盘子数目为 2 ，子字符串中右边两个盘子在它们左边和右边 都 至少有一支蜡烛。
请你返回一个整数数组 answer ，其中 answer[i] 是第 i 个查询的答案。

示例 1:

输入：s = "||***|", queries = [[2,5],[5,9]]
输出：[2,3]
解释：

• queries[0] 有两个盘子在蜡烛之间。
• queries[1] 有三个盘子在蜡烛之间。
  示例 2:
  

输入：s = "||||||*", queries = [[1,17],[4,5],[14,17],[5,11],[15,16]]
输出：[9,0,0,0,0]
解释：

• queries[0] 有 9 个盘子在蜡烛之间。
• 另一个查询没有盘子在蜡烛之间。

提示：

3 <= s.length <= 105
s 只包含字符 '*' 和 '|' 。
1 <= queries.length <= 105
queries[i].length == 2
0 <= lefti <= righti < s.length

思路

假设有一个例子字符串s = '**|***|*'，需要查询q1至q2有多少盘子在两个蜡烛之间

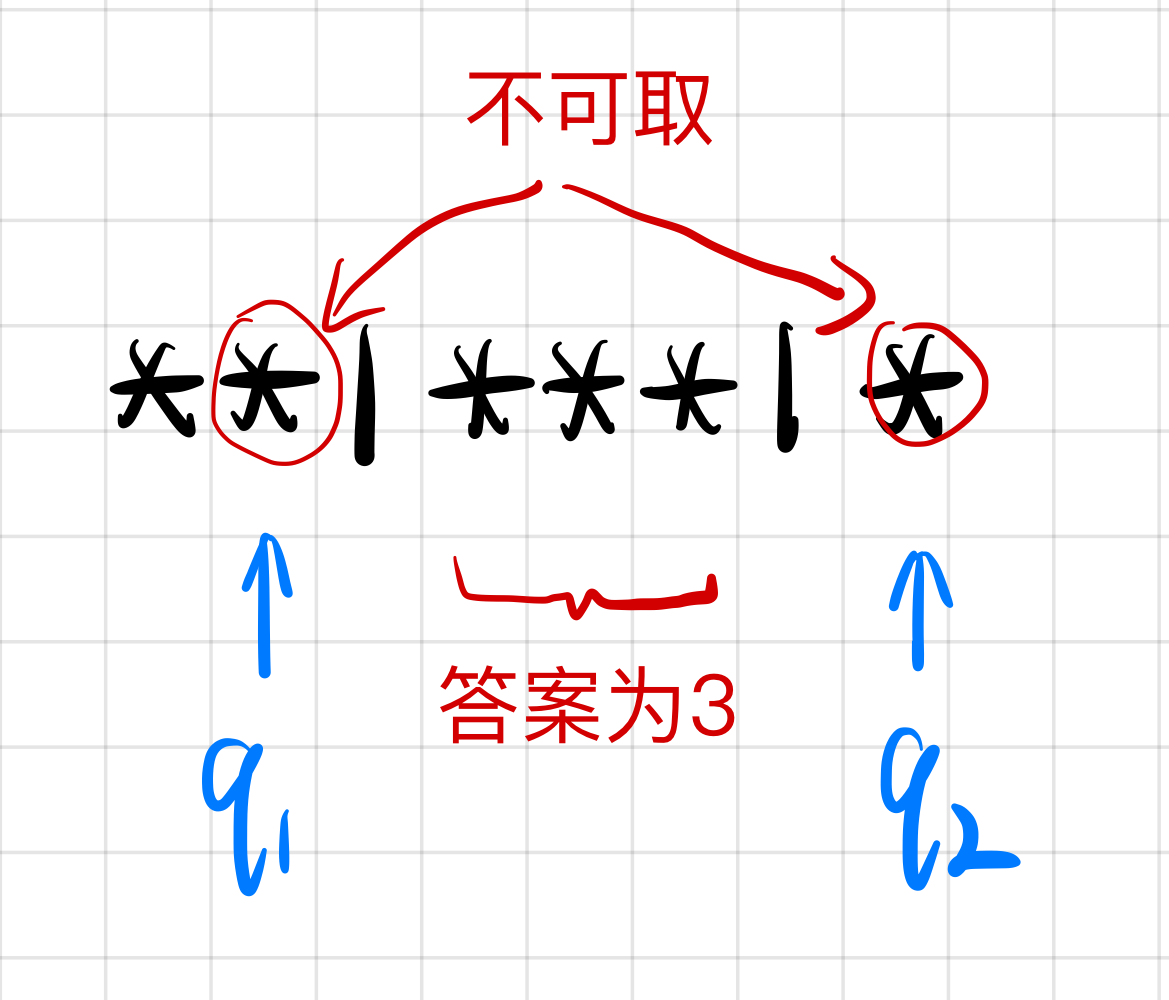
那么我们只需要知道：

1. 从q1到q2总共有多少盘子totalPlants
2. q1开始从左往右数，第一个蜡烛的位置p1
3. q2开始从右往左数，第一个蜡烛的位置p2

之后使用totalPlants - (p1 - q1) - (q2 - p2)，剔除不在蜡烛包围内的盘子数，就可以得到被蜡烛包围的盘子数。

编码思路

1. 如何得到totalPlants？
   使用前缀和统计得到前缀和数组suffixPlate，使用suffixPlate[q2] - (suffixPlate[q1 - 1] ?? 0)即可得到q1到q2之间的盘子数量
2. 如何得到p1、p2的位置？
   • 对于p2，可以使用一个数组lFirstCandle，数组长度与字符串s的长度一样，lFirstCandle[i]表示s[i]的左边最近的蜡烛的位置。这样我们只需要查询lFirstCandle[q2]，就能得到p2的值了
   • 对于p1，可以使用一个数组rFirstCandle，数组长度与字符串s的长度一样，rFirstCandle[i]表示s[i]的右边最近的蜡烛的位置。这样我们只需要查询lFirstCandle[q1]，就能得到p1的值了
3. 边界情况：q1、q2之间只有一根蜡烛或者没有蜡烛
   • q1、q2之间只有一根蜡烛会使得totalPlants - (p1 - q1) - (q2 - p2)结果为0，直接返回0即可
   • q1、q2之间没有蜡烛会使得totalPlants - (p1 - q1) - (q2 - p2)的结果为负数，此时返回0即可

代码&gpt分析

function platesBetweenCandles(s: string, queries: number[][]): number[] {let lFirstCandle: number[] = [];let rFirstCandle: number[] = [];let prefixPlate: number[] = [];// 构建前缀和数组for (const char of s) prefixPlate.push((prefixPlate.at(-1) ?? 0) + (char === "*" ? 1 : 0));let l = 0;let lCandlePosition = -1;let r = s.length - 1;let rCandlePosition = s.length;// 缓存左右侧最近的蜡烛的下标while (s[l]) {if (s[l] === "|") lCandlePosition = l;if (s[r] === "|") rCandlePosition = r;lFirstCandle.push(lCandlePosition);rFirstCandle[r] = rCandlePosition;l++;r--;}return queries.map(([l, r]) => {let totalPlants = prefixPlate[r] - (prefixPlate[l - 1] ?? 0);// 考虑负数情况下的边界情况return Math.max(0, totalPlants - (r - lFirstCandle[r]) - (rFirstCandle[l] - l));});
}

算法逻辑

该算法的核心目的是在一个由蜡烛 (|) 和盘子 (*) 组成的字符串中，根据给定的查询，快速计算两根蜡烛之间盘子的数量。通过预处理构建前缀和数组和左右最近蜡烛位置数组，将每次查询的复杂度从 O(n)O(n)O(n) 降低到 O(1)O(1)O(1)。

---

变量解释

1. lFirstCandle: 数组，用于存储每个字符左侧最近的蜡烛的索引。如果当前位置没有蜡烛，则存储上一个蜡烛的位置。
2. rFirstCandle: 数组，用于存储每个字符右侧最近的蜡烛的索引。如果当前位置没有蜡烛，则存储下一个蜡烛的位置。
3. prefixPlate: 前缀和数组，用于存储从字符串开头到当前位置盘子 (*) 的累计数量。
4. lCandlePosition: 临时变量，用于记录遍历过程中左侧最近的蜡烛的位置。
5. rCandlePosition: 临时变量，用于记录遍历过程中右侧最近的蜡烛的位置。
6. l 和 r: 指针变量，分别从左向右和从右向左遍历字符串。

---

关键代码解析

1. 构建前缀和数组：

   javascript复制代码
   for (const char of s) prefixPlate.push((prefixPlate.at(-1) ?? 0) + (char === "*" ? 1 : 0));
   

   这段代码通过判断每个字符是否是盘子 (*)，计算当前累计的盘子数量，并存储到前缀和数组中。如果字符是蜡烛 (|)，前缀和保持不变。

2. 缓存左右侧最近蜡烛的下标：

   javascript复制代码
   while (s[l]) {if (s[l] === "|") lCandlePosition = l;if (s[r] === "|") rCandlePosition = r;lFirstCandle.push(lCandlePosition);rFirstCandle[r] = rCandlePosition;l++;r--;
   }
   

   双指针分别从字符串两端向中间遍历，记录每个字符左侧和右侧最近的蜡烛位置，并将其存储到 lFirstCandle 和 rFirstCandle 数组中。

3. 处理每个查询：

   javascript复制代码
   return queries.map(([l, r]) => {let totalPlants = prefixPlate[r] - (prefixPlate[l - 1] ?? 0);return Math.max(0, totalPlants - (r - lFirstCandle[r]) - (rFirstCandle[l] - l));
   });
   

   • 通过前缀和数组计算区间内盘子的总数。
   • 减去两端无法被两根蜡烛包围的盘子数量。
   • 使用 Math.max(0, ...) 确保结果非负。

---

性能分析

1. 时间复杂度：
   • 预处理阶段（前缀和数组和左右最近蜡烛数组）：O(n)O(n)O(n)，其中 nnn 是字符串长度。
   • 查询阶段：每次查询是 O(1)O(1)O(1)，总查询复杂度是 O(q)O(q)O(q)，其中 qqq 是查询的数量。
   • 总体时间复杂度：O(n+q)O(n + q)O(n+q)。
2. 空间复杂度：
   • 使用了 prefixPlate、lFirstCandle 和 rFirstCandle，每个数组的大小为 O(n)O(n)O(n)。
   • 总空间复杂度为 O(n)O(n)O(n)。

---

适用场景

1. 字符串区间统计问题：需要在多次查询中高效统计特定字符的数量。

2. 动态规划问题优化：通过预处理构建前缀和数组或最近位置数组来降低查询复杂度。

3. 场景示例

   ：

   • 盘子和蜡烛的场景可用于描述线性排列中的区间统计问题，如铁路站点与列车车厢统计。
   • DNA 序列中某两段标记之间核苷酸的计数问题。