目录
- 概
- 符号说明
- 4-bit FQT
- Learned Step Size Quantization
- Hadamard Quantization
- Bit Splitting and Leverage Score Sampling
- 代码
Xi H., Li C., Chen J. and Zhu J. Training transformers with 4-bit integers. NeurIPS, 2023.
概
本文针对 4-bit 中训练中一些特点 (针对 transformers) 提出了一系列解决方法.
符号说明
- 本文主要考虑 transformer 的 4-bit 量化训练, 其中主要涉及如下的矩阵乘法操作:\[\mathbf{Z} = \mathbf{XW}^T, \quad \mathbf{Z} \in \mathbb{R}^{N \times C}, \mathbf{X} \in \mathbb{R}^{N \times D}, \mathbf{W} \in \mathbb{R}^{C \times D}. \]
4-bit FQT
Learned Step Size Quantization
-
首先, 作者采用 learned step size quantizer (LSQ):
\[\text{int}_{s_X} (\mathbf{X}) := \lfloor \text{clamp}(\mathbf{X} / s_X, -Q_N, Q_P) \rceil, \]其中 \(s_X\) 是可学习的参数, 旨在保证将输入的范围放缩到 \([-Q_N, Q_P]\). 量化后的值属于: \(\{-Q_N, -Q_N + 1, \ldots, Q_P\}\), 对于 4-bit 量化, \(Q_N = Q_P = 7\).
-
反量化过程为:
\[\text{float}(\text{int}_{s_X} (\mathbf{X})) = s_X \text{int}_{s_X}(\mathbf{X}) \approx \mathbf{X}. \] -
给定 LSQ, 量化后的矩阵乘法可以用如下方式近似:
\[\mathbf{Y} = \mathbf{XW}^T \approx s_X s_W \text{int}_{s_X} (\mathbf{X}) \text{int}_{s_W} (\mathbf{W})^T. \]
Hadamard Quantization
-
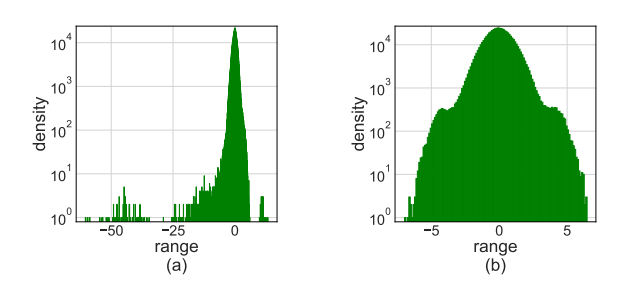
但是, 单纯使用 LSQ 会产生很大的误差, 主要原因是, 数据的分布如上图 (a) 所示极不均匀, 所以提出用 Hadamard matrix 来进行一个 smooth.
-
Hadamard matrix 是一个 \(2^k \times 2^k\) 大小的正交矩阵:
\[\mathbf{H}_0 = [1], \quad \mathbf{H}_k = \frac{1}{\sqrt{2}} \left [\begin{array}{cc}\mathbf{H}_{k-1} & \mathbf{H}_{k-1} \\\mathbf{H}_{k-1} & -\mathbf{H}_{k-1}\end{array} \right ]. \]容易证明 \(\mathbf{H}_k \mathbf{H}_k = \mathbf{I}\). 如 (b) 所示, 明显分布更加均匀了.
-
而且, 这种方式下的量化矩阵乘法的计算也是方便的:
\[\mathbf{Y} = \mathbf{XW}^T \approx s_X s_W \text{int}_{s_X} (\mathbf{XH}) \underbrace{\mathbf{HH}^T}_{=\mathbf{I}} \text{int}_{s_W} (\mathbf{WH})^T. \]
Bit Splitting and Leverage Score Sampling
- 在 Backpropagation 过程中, 作者发现, transformers (但是卷积网络不行) 的梯度呈现出明显的结构稀疏性, 经常一整行为 0. 作者选择抛弃对很小的梯度的量化, 用省下的空间去建模那些较大的值. 这些操作通过 bit splitting 和 leverage score sampling 实现. 感兴趣的请回看原文.
代码
[official-code]