「NOIP2024」 树上查询

update 2024/12/28

题目描述

给定一棵树，每次询问区间 \([l,r]\) 的

\[\max_{l \le l' \le r' \le r \land r' - l' + 1 \ge k}\text{dep}_ {\text{LCA*}(l', r')} \]

引理证明

先来证两个区间 \(\text{LCA}\) 的引理：
对于 \(\text{LCA} \{ l, l + 1, \dots r\}\) 我们有 \(\text{LCA} \{ l, l + 1, \dots r\}\) 为 \([l, r]\) 中 \(\text{dfs}\) 序最小的点和最大的点的 \(\text{LCA}\) 。证明：
假设点 \(u\) 是区间 \([l, r]\) 中 \(\text{dfs}\) 序最小的点 \(i\) 和最大的点 \(j\) 的 \(\text{LCA}\) ，则 \(dfn_u \leq dfn_i \leq dfn_j \leq out_u\)。于是我们对于区间 \([l, r]\) 中任意一个点 \(v\) 有 \(dep_i \leq dep_v \leq dep_j\)，则 \(dep_u \leq dep_v \leq out_u\) ，所以区间中所有点都在 \(u\) 的子树中。

---

此外我们有 \(\text{LCA} \{ l, l + 1, \dots , r \}\) 为所有 \(\text{LCA(i, i + 1)} (l \leq i < r)\) 中最靠近根节点的那个。证明：
记 \(c_i = dep_{\text{LCA}(i, i + 1)}\) ，则对于结点 \(u\) ，\(v\) 若 \(dep_u \leq dep_v\) 可以说点 \(u\) 比点 \(v\) 更靠近根节点。设点 \(u\) 是区间 \([l, r]\) 的 \(\text{LCA}\) ，则一定存在两个点 \(x\) ，\(y\) 来自 \(u\) 的不同子树，此时 \([x, y)\) 中一定存在一个 \(v\) 使得 \(v\) 和 \(v + 1\) 来自不同子树，即 \(c_v = dep_u\) ，此时 \(\text{LCA} (v, v + 1) = u\) 。

思路推导

首先，对于区间 \(\text{LCA}\) ，我们已知有两个求法了，在此题中，如果要找 \(\text{dfs}\) 序最小最大需要额外维护一次最大最小，是没有前途的，所以针对第二种方法进行优化。
将 \(i\) 和 \(i + 1\) 两点的 \(dep_{\text{LCA}}\) 作为 \(c_i\) ，问题就转化为对于每个区间求

\[\max_{l \le l' \le r' \le r \land r' - l' + 1 \ge k}{\max_{l' \leq i < r'}{c_i}} \]

对于 \(k = 1\) 的情况额外用 \(\text{RMQ}\) 处理。
首先我们很容易想到的是对于区间长度大于 \(k\) 的一定不优于区间长度等于 \(k\) 的，这一点很好证明，于是式子就变成

\[\max_{l \le l' \le r' \le r \land r' - l' + 1 = k}{\max_{l' \leq i < r'}{c_i}} \]

一个相对来说比较容易想到的方法是计算每个点作为 \(\text{LCA}\) 的贡献。对于任意一个 \(i\) ，我们定义 \(pre_i\) 表示在 \(i\) 左边第一个 \(j + 1\) 使得 \(c_j \leq c_i\) ，\(suf_i\) 表示在 \(i\) 右边第一个 \(j - 1\) 使得 \(c_j < c_i\)（这一定是左边取 \(\leq\) 右边取 \(<\) 或左边取 \(<\) 右边取 \(\leq\)，原因后文再说），这可以通过单调栈求取。对于 \(i\) ，能产生贡献的区间为 \(l=[pre_i + 1 , i]\) ，\(r=[i , suf_i - 1]\) ，容易想到转化为二位数点问题，该贡献区间可转化为以下矩形:

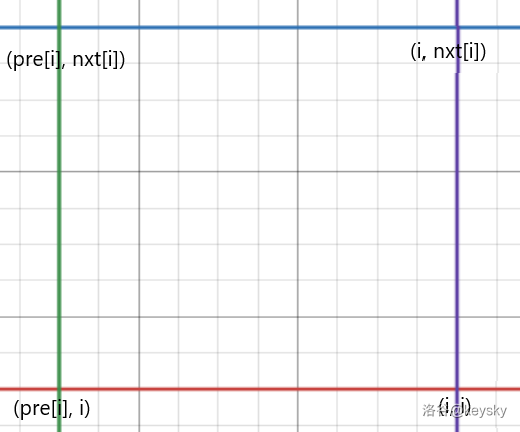
对于查询，也就转换为了一条斜率为 \(1\) 的线段，如下图：

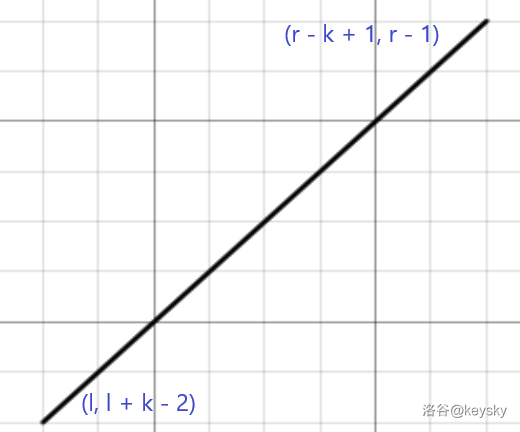
显然对于 \(3\) 个方向的扫描线我们是没法维护的（至少我不知道），所以我们要将其拆分。
对于查询的线段，我们把它分为两个情况：

• 全部被包含于一个矩形
• 跨越多个矩形

对于第 \(1\) 种情况，扫描线板子解决。
对于第 \(2\) 种情况，我们可以发现如果该线段跨越矩阵的话一定会与矩形的边界有交点，于是我们可以只保留矩形的 \(4\) 条边，再拆分为横向和竖向的 \(2\) 对边，加上查询的斜线，就转换为两遍分别有两个方向的扫描线，如下图：
横向边贡献 \(+\) 查询

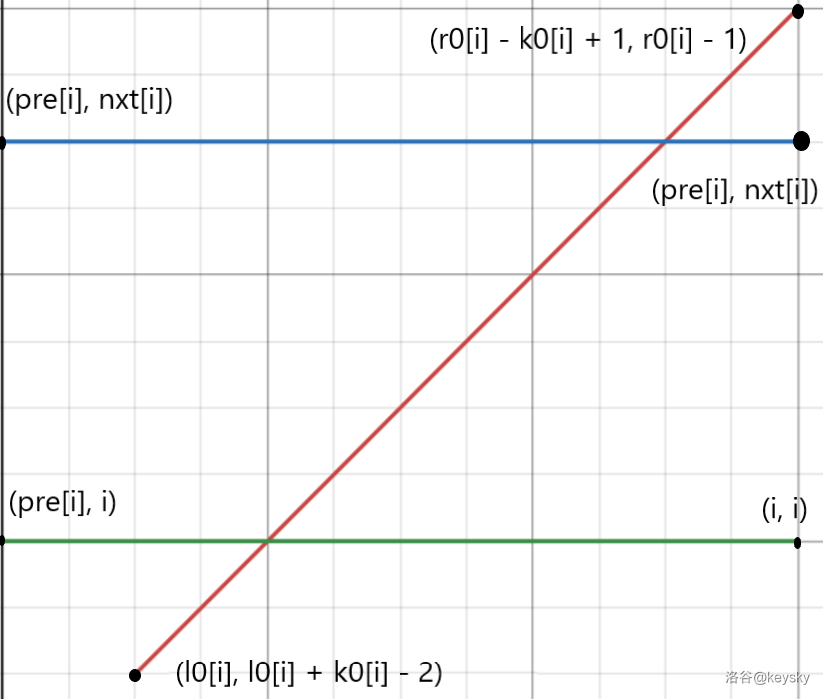
竖向边贡献 \(+\) 查询

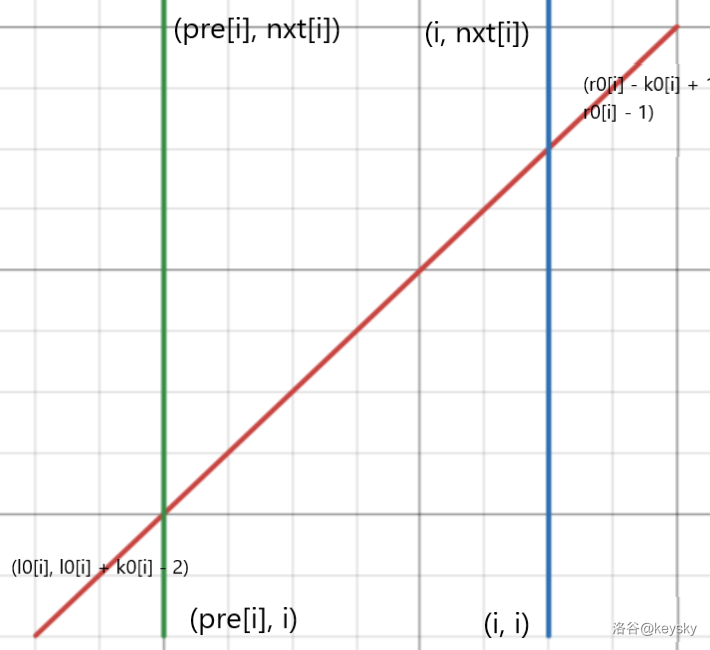
但我们看到对于查询线段是斜着的，是不能用扫描线查询的，但整张图中是只有两个方向的，所以可以想到通过旋转坐标轴的 \(\hat{i}\) 和 \(\hat{j}\) 来拉平查询线段使得所有线“横平竖直”。
对于第 \(2\) 张图拉直过后像这样：

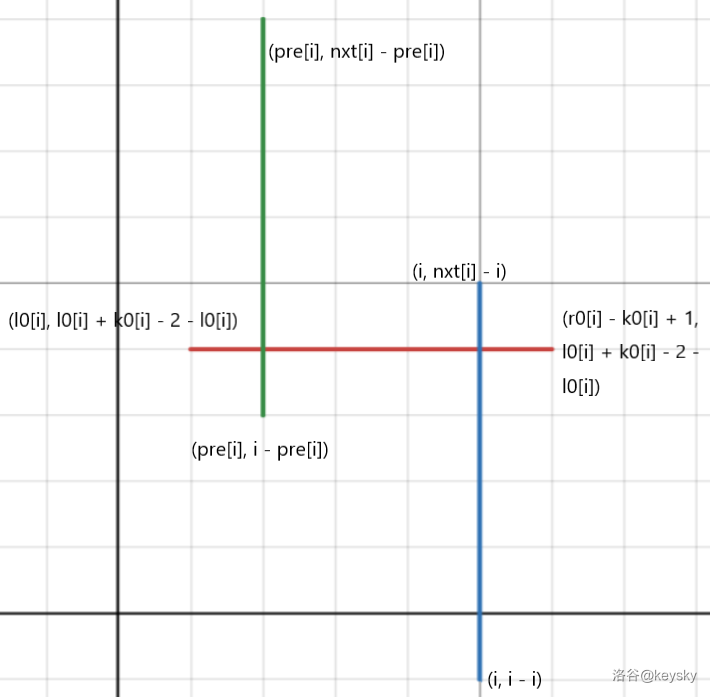
对于第一张图留给读者思考（才不是因为我不想画了）
最后还有一个问题：扫描线取最大值的影响怎么消除，这就关系到前文提到关于区间边界的问题了，正常情况下所有贡献矩形是不会产生交集的（原因可以自己手推一下一对 \(i,j\) 使得 \(i \leq j\) ，\(c_i < c_j\) 和 \(c_j < c_i\)的两种情况），除非出现两个 \(c_i\) 相等，此时如前文所述改为类似左闭右开的方法便可令其也不产生交集同时不重不漏。此时维护扫描线即可区间覆盖，区间取 \(\max\) 了。
所以统共来说是 \(3\) 遍扫描线 \(+\) \(1\) 遍 \(\text{RMQ}\)，还是比较恶心的（当然是我的思路和做法有些复杂了，其它还有些相对更简便的做法）。

解法概括

对于点 \(i\) 定义 \(c_i\) 为 \(dep_{\text{LCA}(i,i + 1)}\) ，转换为序列问题。
若 \(k \geq 2\) 则对于 \(c_i\) 产生的贡献矩形将其拆分为两对相互平行的线段，旋转坐标轴，让查询斜线变为横线或竖线，进行 \(2\) 遍扫描线，再与线段一端点值取 \(\max\) ，对于 \(k = 1\) 的情况跑一遍 \(\text{RMQ}\) ，最后统计答案

实现

注意一些关于下标、边界的实现细节。
我之前是将线段树的功能全用区修区查来实现的，同时扫描线无论特殊性全写在 solve 中，第一次过了，没注意 \(1.98s\) 的时间，后来再交就一直 \(\text{TLE}\) ，于是修改了一些不必要的懒标记和区修，哪怕删了注释的调试，代码还是多了三十几行，但能保证不 \(\text{TLE}\) 了。
对于我这个思路，理论时间复杂度为 \(O(N log N)\) ，但常数巨大，按最坏情况分析：扫描线 \(4\) 倍，线段树 \(4\) 倍，\(3\) 遍扫描线，总计 \(\times 48\) ，但实际只有大约一半的常数。

#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
int n, q;
vector<int>G[N];
struct line {int x, y, k;bool operator < (const line& o)const { return x == o.x ? k < o.k : x < o.x; }
}li[N << 2];
struct node {int x, dy, ty, k;bool operator < (const node& o)const { return x == o.x ? k < o.k : x < o.x; }
}li2[N << 2];
struct query {int x, l, r, id;bool operator < (const query& o)const { return x < o.x; }
}qry[N];
int ans[N];
struct SegmentTree {
#define ls (id << 1)
#define rs (id << 1 | 1)
#define mid (l + r >> 1)struct Segment {int mx;}seg[N << 2];inline void merge(int id) { seg[id].mx = max(seg[ls].mx, seg[rs].mx); }inline void build(int id, int l, int r) {seg[id].mx = 1;if (l == r) return;build(ls, l, mid);build(rs, mid + 1, r);}inline void pushdown(int id) {if (seg[id].mx != -1) {seg[ls].mx = seg[id].mx;seg[rs].mx = seg[id].mx;seg[id].mx = -1;}}inline void change(int id, int l, int r, int x, int k) {if (l == r) {seg[id].mx = k;return;}if (x <= mid) change(ls, l, mid, x, k);else change(rs, mid + 1, r, x, k);merge(id);}inline int query(int id, int l, int r, int L, int R) {if (l >= L && R >= r) return seg[id].mx;int ret = 1;if (L <= mid) ret = max(ret, query(ls, l, mid, L, R));if (R > mid) ret = max(ret, query(rs, mid + 1, r, L, R));return ret;}inline void modify(int id, int l, int r, int L, int R, int k) {if (l >= L && R >= r) {seg[id].mx = k;return;}pushdown(id);if (L <= mid) modify(ls, l, mid, L, R, k);if (R > mid) modify(rs, mid + 1, r, L, R, k);}inline int get(int id, int l, int r, int x) {if (l == r) return seg[id].mx;pushdown(id);if (x <= mid) return get(ls, l, mid, x);else return get(rs, mid + 1, r, x);}
}SGT;
const int K = 21;
int up[K + 1][N], dep[N];
inline void dfs(int u, int fa) {for (int i = 1;i < K;i++)up[i][u] = up[i - 1][up[i - 1][u]];for (auto v : G[u]) {if (v == fa) continue;up[0][v] = u;dep[v] = dep[u] + 1;dfs(v, u);}
}
inline void lift(int& x, int k) {for (int i = K - 1;i >= 0;i--)if (k >> i & 1) x = up[i][x];
}
inline int lca(int a, int b) {lift(a, dep[a] - min(dep[a], dep[b]));lift(b, dep[b] - min(dep[a], dep[b]));if (a == b) return a;for (int i = K - 1;i >= 0;i--)if (up[i][a] != up[i][b]) a = up[i][a], b = up[i][b];return up[0][a];
}
int l0[N], r0[N], k0[N];
int pre[N], nxt[N], c[N];
int stk[N], top;
int qc, m;
inline void solve() {sort(qry + 1, qry + qc + 1);sort(li + 1, li + m + 1);SGT.build(1, 1, n);int j = 1;for (int i = 1;i <= qc;i++) {while (li[j].x <= qry[i].x && j <= m) {SGT.change(1, 1, n, li[j].y, li[j].k);j++;}ans[qry[i].id] = max(ans[qry[i].id], SGT.query(1, 1, n, qry[i].l, qry[i].r));}
}
int ST[K + 1][N], LG[N];
inline void init() {for (int i = 2;i <= n;i++) LG[i] = LG[i >> 1] + 1;for (int i = 1;i <= n;i++) ST[0][i] = dep[i];for (int i = 1;i < K;i++)for (int j = 1;j + (1 << i) - 1 <= n;j++)ST[i][j] = max(ST[i - 1][j], ST[i - 1][j + (1 << i - 1)]);
}
inline int RMQ(int l, int r) {int i = LG[r - l + 1];return max(ST[i][l], ST[i][r - (1 << i) + 1]);
}
int main() {// freopen("query.in", "r", stdin);// freopen("query.out", "w", stdout);scanf("%d", &n);for (int i = 1;i < n;i++) {int u, v;scanf("%d%d", &u, &v);G[u].push_back(v);G[v].push_back(u);}scanf("%d", &q);for (int i = 1;i <= q;i++) scanf("%d%d%d", &l0[i], &r0[i], &k0[i]);dep[1] = 1;dfs(1, 0);for (int i = 1;i < n;i++) c[i] = dep[lca(i, i + 1)];// for (int i = 1;i < n;i++) printf("%d ", c[i]);// puts("");stk[++top] = 0;for (int i = 1;i < n;i++) {while (c[stk[top]] >= c[i] && top > 0) top--;pre[i] = stk[top] + 1;stk[++top] = i;}top = 0;stk[++top] = n;for (int i = n - 1;i >= 1;i--) {while (c[stk[top]] > c[i] && top > 0) top--;nxt[i] = stk[top] - 1;stk[++top] = i;}// for (int i = 1;i < n;i++) printf("%d ", pre[i]);// puts("");// for (int i = 1;i < n;i++) printf("%d ", nxt[i]);// puts("");/*matrix: (pre[i], nxt[i]) -------- (i, nxt[i])(pre[i], i) ------------------(i, i)line:(r0[i] - k0[i] + 1, r0[i] - 1)/////////(l0[i], l0[i] + k0[i] - 2)*/m = qc = 0;for (int i = 1;i < n;i++) {li[++m] = { pre[i] - nxt[i],nxt[i],c[i] };li[++m] = { i + 1 - nxt[i],nxt[i], 1 };li[++m] = { pre[i] - i,i,c[i] };li[++m] = { i + 1 - i,i,1 };}for (int i = 1;i <= q;i++)if (k0[i] > 1)qry[++qc] = { l0[i] - (l0[i] + k0[i] - 2),l0[i] + k0[i] - 2,r0[i] - 1,i };solve();/*matrix: (pre[i], nxt[i])          (i, nxt[i])|                           ||                           ||                           ||                           ||                           ||                           |(pre[i], i)                  (i, i)line:(r0[i] - k0[i] + 1, r0[i] - 1)/////////(l0[i], l0[i] + k0[i] - 2)*/m = qc = 0;for (int i = 1;i < n;i++) {li[++m] = { i - pre[i],pre[i],c[i] };li[++m] = { nxt[i] + 1 - pre[i],pre[i],1 };li[++m] = { i - i,i,c[i] };li[++m] = { nxt[i] + 1 - i,i,1 };}for (int i = 1;i <= q;i++)if (k0[i] > 1)qry[++qc] = { l0[i] + k0[i] - 2 - l0[i],l0[i],r0[i] - k0[i] + 1,i };solve();/*matrix: (pre[i], nxt[i]) -------- (i, nxt[i])|                           ||                           ||                           ||                           ||                           ||                           |(pre[i], i) ------------------(i, i)line:.(l0[i], l0[i] + k0[i] - 2)*/m = qc = 0;for (int i = 1;i < n;i++) {li2[++m] = { pre[i],i,nxt[i],c[i] };li2[++m] = { i + 1,i,nxt[i],1 };}for (int i = 1;i <= q;i++)if (k0[i] > 1)qry[++qc] = { l0[i],l0[i] + k0[i] - 2,l0[i] + k0[i] - 2,i };// for (int i = 1;i <= m;i++) printf("%d %d %d %d\n", li[i].x, li[i].dy, li[i].ty, li[i].k);sort(qry + 1, qry + qc + 1);sort(li2 + 1, li2 + m + 1);SGT.build(1, 1, n);int j = 1;for (int i = 1;i <= qc;i++) {while (li2[j].x <= qry[i].x && j <= m) {SGT.modify(1, 1, n, li2[j].dy, li2[j].ty, li2[j].k);j++;}ans[qry[i].id] = max(ans[qry[i].id], SGT.get(1, 1, n, qry[i].l));}init();for (int i = 1;i <= q;i++)if (k0[i] == 1) ans[i] = max(ans[i], RMQ(l0[i], r0[i]));for (int i = 1;i <= q;i++) printf("%d\n", ans[i]);return 0;
}