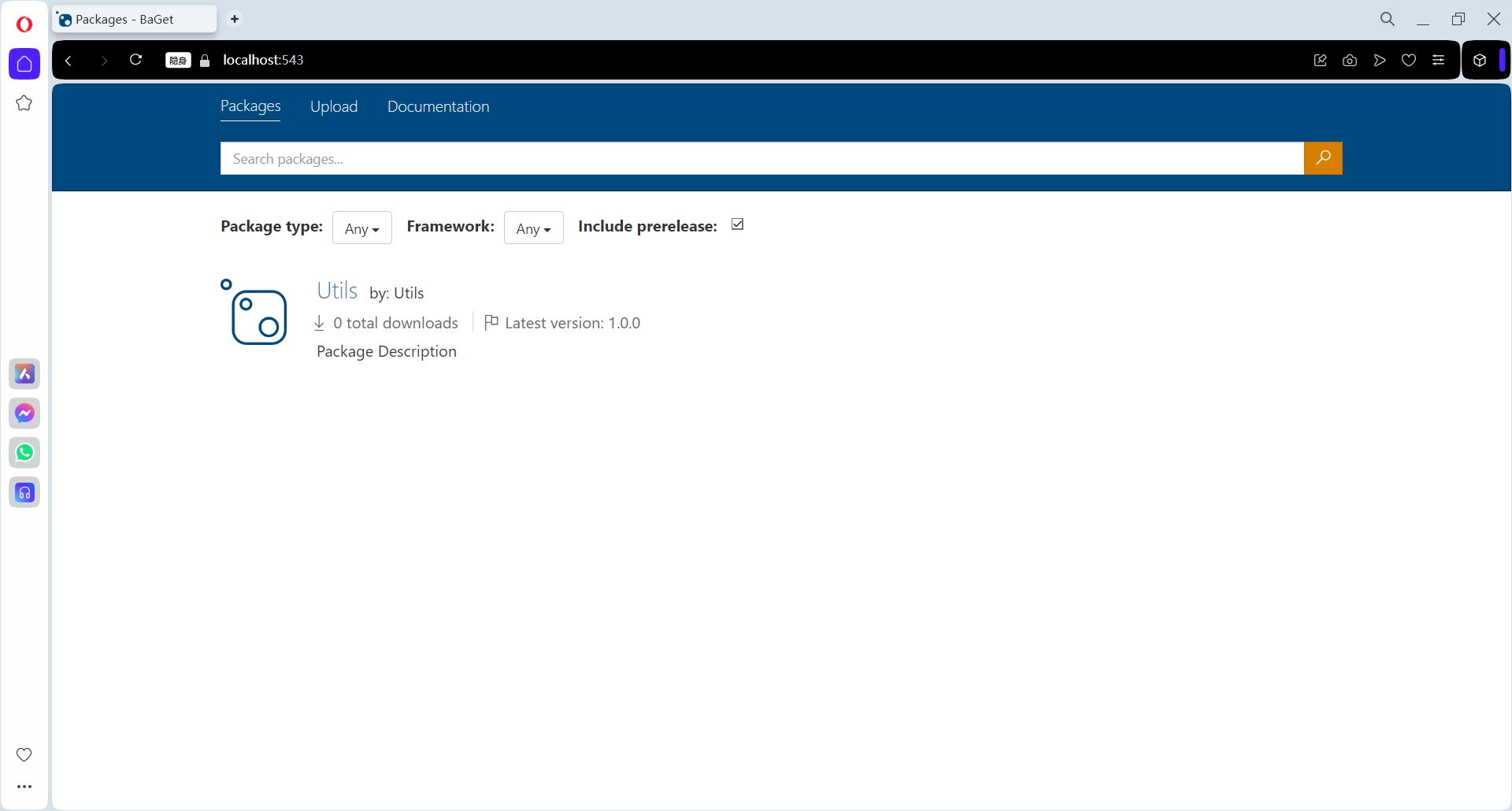
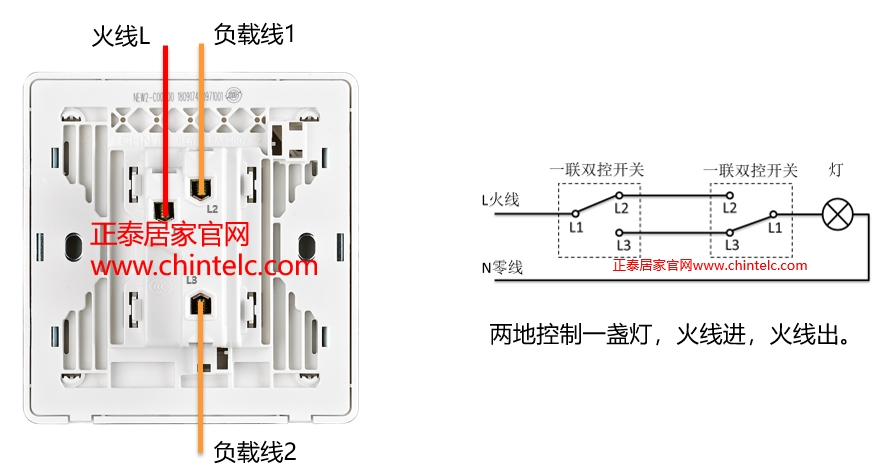
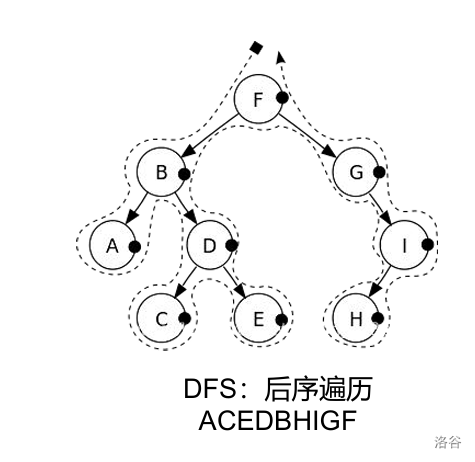
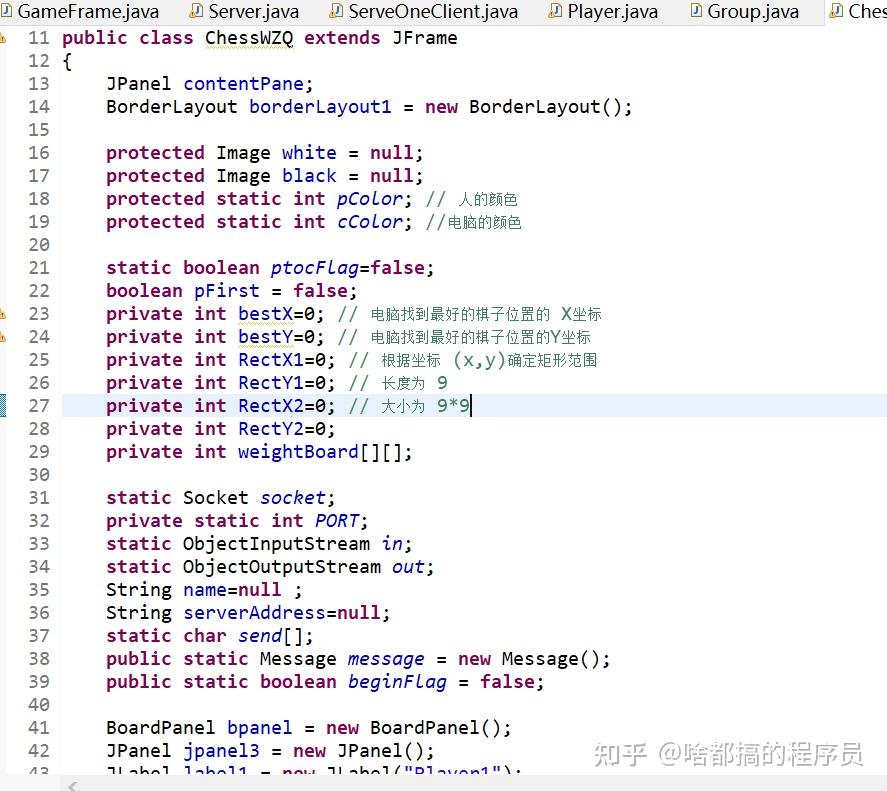
题目:

思路:
很明显总的情况是2^h*w种,然后不难发现改变一行只会影响到相邻两行,也就是说前面的决策不会影响到后面的决策,只有当前面的决策全部合理才能走后一步。
所以取dp:dp[i][j][k]为前i行,j(当前行是1/0否改变),k(当前行的前一行是1/0否改变)。
所以有递推式:dp[i][j][k]=min(dp[i-1][k][l]+j,dp[i][j][k])。
此时k对应的是i-1行的状态。
最后检查:四种状态下,最后一行是否满足(之所以要检查是因为前面只检查到i-1行的合法性),如果满足就取最小值,注意题目最多翻转h次,所以可以设置大数来检验是否有效。
代码:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<algorithm>
#include<queue>
#include<map>
#include<string.h>
#include<string>
#include<vector>
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
#define int long long
const int INF = 0x3f3f3f3f3f3f;
const int N = 1e3 + 10;
int h, w;
int mp[N][N];
int delta[][2] = {{0,1},{0,-1},{1,0},{-1,0}};
//前i行是否操作的最小次数
int dp[N][2][2];//判断第x行是否有孤立点,无孤立点就true
bool jd(int x,int bef,int now,int nx)
{for (int i = 1; i <= w; i++){int cntb = 0;for (int j = 0; j < 4; j++){int dx = delta[j][0], dy = delta[j][1];int nowVal = (now) ? 1 - mp[x][i] : mp[x][i];if (x + dx > 0 and x + dx <= h and i + dy > 0 and i + dy <= w){int jdval = 0;int y = i + dy;if (dx == -1)jdval = (bef) ? 1 - mp[x + dx][y] : mp[x + dx][y];else if (dx == 1)jdval = nx ? 1 - mp[x + dx][y] : mp[x + dx][y];else jdval= (now) ? 1 - mp[x][y] : mp[x][y];if (jdval == nowVal)cntb++;}}if (cntb == 0)return false;}return true;
}signed main()
{IOS;cin >> h >> w;for (int i = 1; i <= h; i++)for (int j = 1; j <= w; j++)cin >> mp[i][j];memset(dp, INF, sizeof(dp));//首先确定前两行的情况,然后再递推后面的,dp[1][1][0] = 1;dp[1][0][0] = 0;for (int i = 2; i <= h; i++){for (int j = 0; j < 2; j++){for (int k = 0; k < 2; k++){for (int l = 0; l < 2; l++){if (jd(i - 1, k, j, l))dp[i][l][j] = min(dp[i - 1][j][k] + l, dp[i][l][j]);}}}}//最后检验最后一行是否能没有孤立点int ans = INF;for (int i = 0; i < 2; i++)for (int j = 0; j < 2; j++)if (jd(h, j, i, 0))ans = min(ans, dp[h][i][j]);if (ans <=h)cout << ans;else cout << -1;return 0;
}