树枝边:DFS时经过的边,即DFS搜索树上的边。
前向边:与DFS方向一致,从某个结点指向其某个子孙的边。
后向边:与DFS方向相反,从某个结点指向其某个祖先的边。(返祖边)
横叉边:从某个结点指向搜索树中的另一子树中的某结点的边。
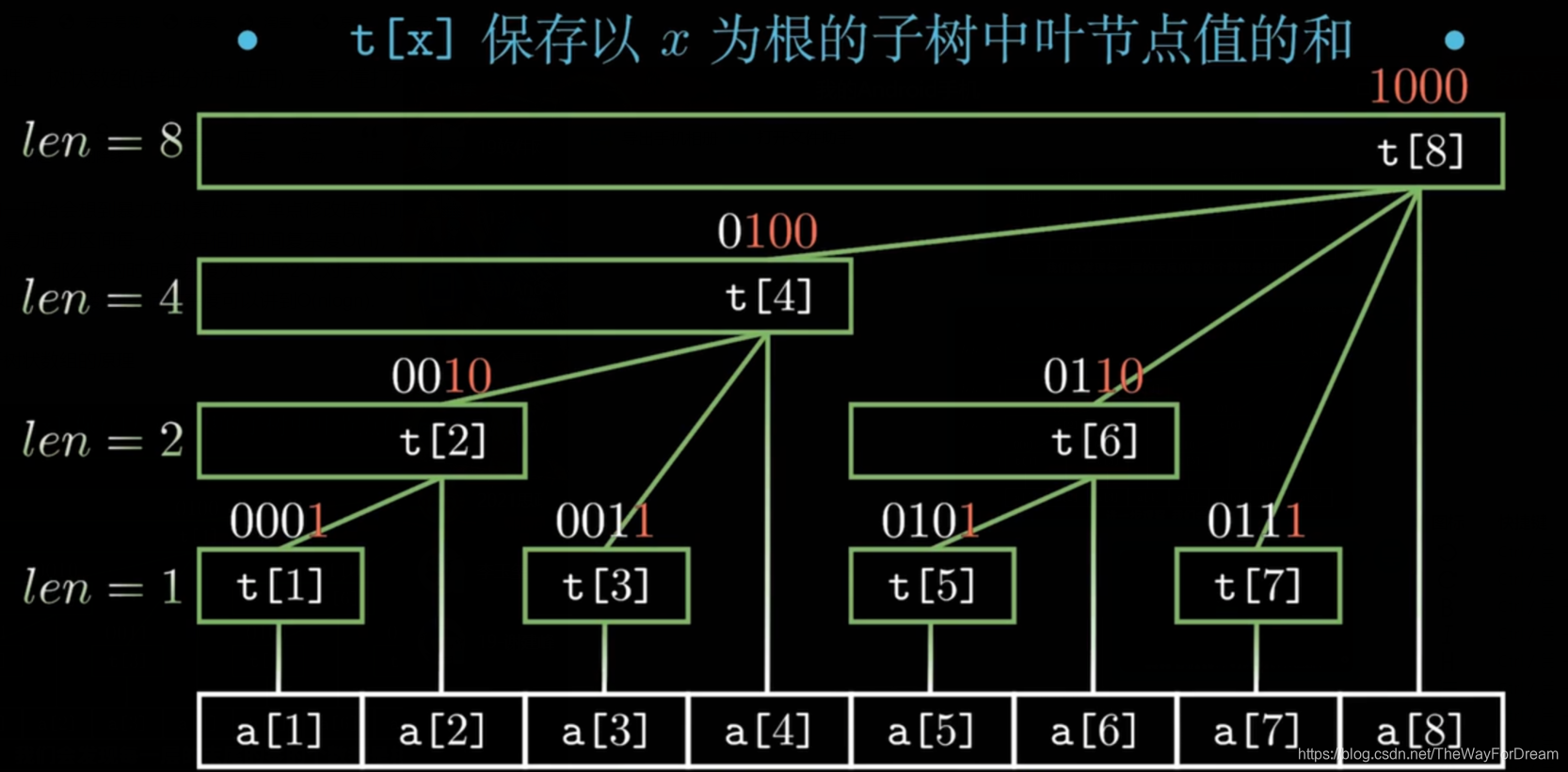
Tarjan算法是基于对图深度优先搜索的算法.
每个强连通分量为搜索树中的一棵子树。
搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。
由定义可以得出,
Low(u)=Min {Low(u), Low(v) } (u,v)为树枝边,u为v的父节点 .
Low(u)=Min {Low(u), DFN(v) } DFN(v),(u,v)为指向栈中节点的后向边(指向栈中结点的横叉边) }
当结点u搜索结束后,若DFN(u)=Low(u)时,则以u为根的搜索子树上所有还在栈中的节点是一个强连通分量。
void Tarjan(int x)
{dfn[x] = low[x] = ++timer;stak[++top] = x;for (int i = head[x]; i; i = nxt[i]){int v = to[i];if (!dfn[v]) // 没有遍历过是树枝边{Tarjan(v);low[x] = min(low[x], low[v]);}else if (!col[v]) // v在栈中{low[x] = min(low[x], dfn[v]);}}if (dfn[x] == low[x]){cnt++;while (stak[top] != x)col[stak[--top]] = cnt;top--;}
}