闲话
我怎么感觉我读了这个论文,还不知道 kernel method 是啥啊。
没人总结这个,可能未来要读一些新东西。
推歌:时间的彼端 by 暗猫の祝福 et al.
the Kernel Method: a collection of examples 读后感
\(1.\) 第一次出现
在 H. Prodinger 看来,kernel method 发源于 Knuth 的书《计算机程序设计艺术・卷1:基础算法》的习题 2.2.1.-4。之后,该方法在论文 Generating functions for generating trees 中被总结。在此,我们首先重现 Knuth 最初的习题,来引入 kernel method。
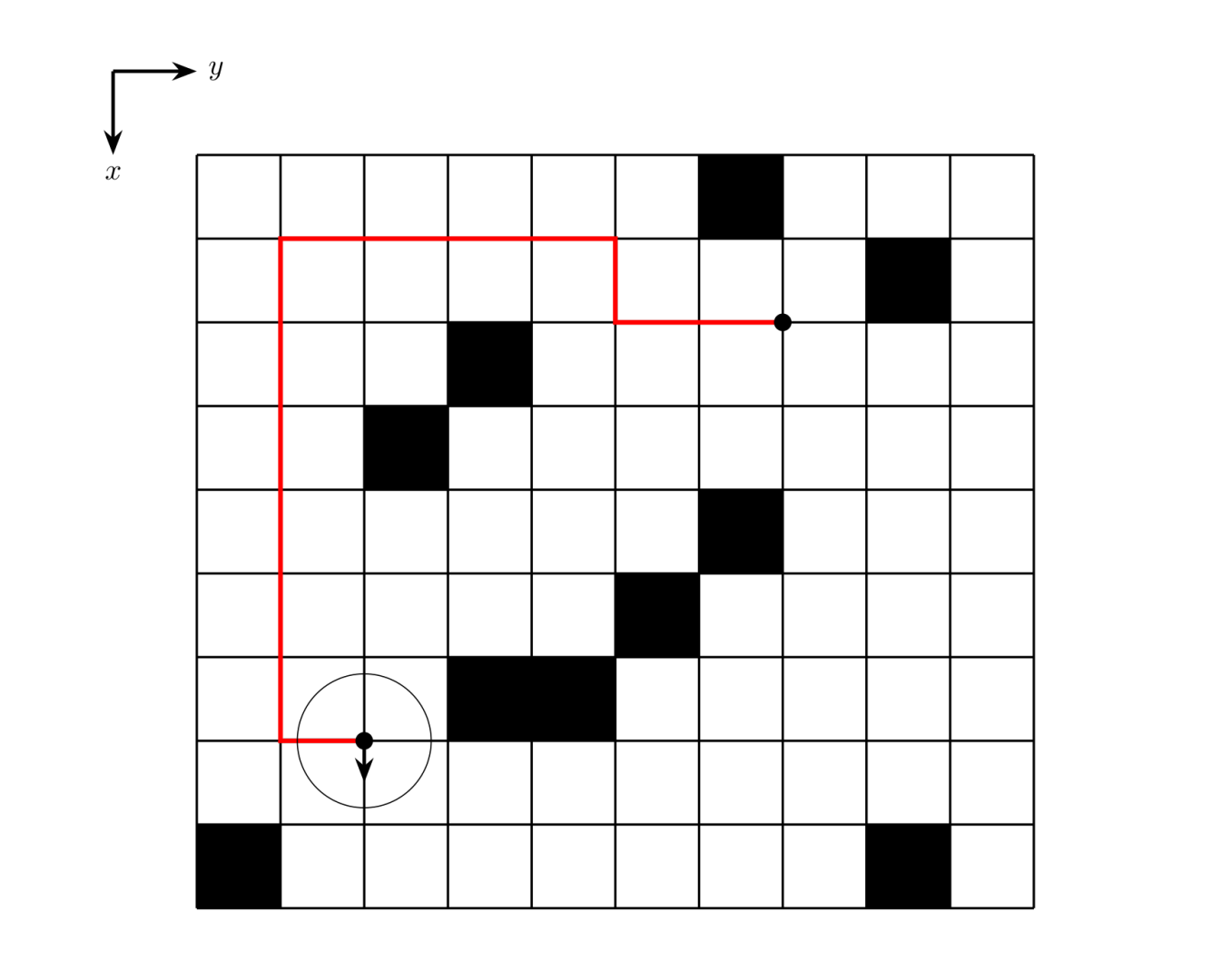
模型是这样的:在直角坐标系上,从原点出发,每次可以从 \((n, m)\) 走到 \((n + 1, m \pm 1)\),但不能越过 \(x\) 轴,即从 \((n, 0)\) 只能走到 \((n + 1, 1)\)。这也叫 Dyck 路。我们的目的是计数从原点出发、到达 \((n, m)\) 的路径。
我们接下来的重点就是 Knuth 所使用的推导方法。不妨建立生成函数 \(f_m(z)\),其中 \([z^n]f_m(z)\) 是我们的目标。那么立得如下的递归关系:
\[\begin{aligned}
f_m(z) &= zf_{m-1}(z) + zf_{m + 1}(z), \qquad m\ge 1 \\
f_m(z) &= 1 + zf_{1}(z)
\end{aligned}
\]
随后引入 \(F(z, x) = \sum_{m\ge 0} f_m(z) x^m\),那么据递推,写出
\[F(z,x) = zx F(z,x) + \dfrac zx \left[F(z,x) - f_0(z) - xf_1(z) \right] + f_0(z)
\]
化简得到(\(f_0(z) = F(z, 0)\))
\[F(z,x) = zx F(z, x) - \dfrac zx\left[F(z, x) - F(z_0)\right] + 1
\]
据此 \(F(z,x) = \dfrac{z F(z, 0) - x}{zx^2 - x + z}\)。我们不能朴素地带入 \(x = 0\) 来解出 \(F(z,0)\),因为这只会得到恒等式。但分解分母为 \(z\left(x - r_1(z)\right)\left(x - r_2(z)\right)\),其中
\[r_{1,2}(z) = \dfrac{1 \mp \sqrt{1 - 4z^2}}{2z}
\]
注意到 \(x,z\to 0\) 时 \(x - r_1(z) \sim x - z\),故 \(F(z,x)\) 的因式 \(\left(x - r_1(z)\right)^{-1}\) 在 \((0, 0)\) 的邻域内没有幂级数展开式,但 \(F(z,x)\) 必然有,故这个“劣”的因式实际上必然不存在,即 \(x - r_1(z)\) 也是分子的因式。那么将分子视作 \(f(x)\),则自然有 \(f(r_1(z)) = 0\),从而得到 \(z F(z,0) - r_1(z) = 0\),因此约掉共同的 \(x-r_1(z)\) 得到
\[F(z,x) = \dfrac{-1}{z(x-r_2(z))} = \dfrac{2}{1-2xz+\sqrt{1-4z^2}}
\]
那么显然地,走到 \((2n, 0)\) 的方案数,或 Catalan 数,即
\[[z^{2n}]F(z,0) = \dfrac 1 {n + 1} \binom{2n}n
\]
相似地,到达 \((n, m)\)(显然应有 \(n\equiv m \pmod 2\))的方案数为
\[[x^mz^n] F(z,x) = [z^{n + 1}] \left(\dfrac{2z}{1+\sqrt{1-4z^2}}\right)^{m + 1} = \dfrac{m+1}{n+1} [z^{n-m}] (1+z^2)^{n+1} = \dfrac{m + 1}{n+1} \binom{n+1}{\frac{n-m}{2}}
\]
\(2.\) Knödel 游走
Knödel 构造了一个简单的装箱问题,其形式可以转化为特殊图上的随机游走。有大小为 \(1\) 的箱子,以及随机到来的大小为 \(\frac{k}{d}, k = 1,\dots,d-1\) 的物品,以及一个在线的、目的是尽可能装满更多箱子的策略。这个问题可以用“状态”来描述,每个状态都编码了某个特定时刻中部分装满的箱子。我们在下面处理了 \(d = 3,4\) 的情况。更大的 \(d\) 会导出十分复杂的情况,我们不处理。
在最简单的版本里,箱子的大小为 \(1\),物品的大小为 \(\frac 13\) 或 \(\frac 23\),两种物品随机到来。有一个人想要在线地装满尽可能多的箱子,这样本质上会剩下一系列装了 \(\frac 23\) 的箱子,我们会将其减少或增加到 \(1\)。这个模型可以自然地被抽象为在一个特殊的无穷图上、从状态 \(0\)(下层最左侧的节点)开始的随机游走(又名 Knödel 游走,以纪念其创造者)。上述特殊图是
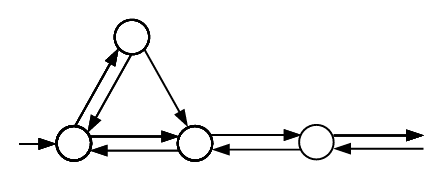
在这个情况中,会有一个特殊的状态 \(\beta\)(上层的唯一节点),表示一个装了 \(\frac 13\) 的箱子。
我们的目的是找到一个二元生成函数,其系数编码了在图上游走的步数与随机游走最终到达的状态。从这里,可以得到每个状态未利用的空间:状态 \(0\) 为 \(0\),状态 \(\beta\)(一个装了 \(1/3\) 的箱子)为 \(2/3\),状态 \(k\)(\(k\) 个装了 \(2/3\) 的箱子)为 \(k / 3\)。
令 \(f_a(z)\) 为生成函数,其中 \([z^n] f_a(z)\) 计数了所有走了 \(n\) 步、终止于状态 \(a\)(\(a \in \mathbb N\) 或 \(a = \beta\))的游走路径。图上的边表示了所有可能的转移,走一步在生成函数上表示为乘 \(z\),立得
\[\begin{aligned}
f_k(z) & = z f_{k - 1} (z) + z f_{k + 1}(z) , \quad k\ge 2 \\
f_1(z) & = z f_0(z) + z f_\beta(z) + z f_2(z) \\
f_0(z) & = 1 + z f_1(z) + z f_\beta(z) \\
f_\beta(z) & = zf_0(z)
\end{aligned}
\]
引入二元生成函数 \(F(z,x) = \sum_{m\ge 0} f_m(z) x^m\),那么使用 \(1.\) 中的 \(r_{1,2}(z)\) 的定义有
\[\begin{aligned}
F(z,x) & = zxF(z,x) + \dfrac zx \left[F(z,x) - f_0(z)\right] + 1 + (1 + x) z f_\beta(z) \\
& = zxF(z,x) + \dfrac zx \left[F(z,x) - F(z,0)\right] + 1 + (1 + x) z^2 F(z, 0) \\
& = \dfrac{z(1 - x(1 + x)z) F(z,0) - x}{zx^2 - x + z} = \dfrac{z(1 - x(1 + x)z) F(z,0) - x}{z\left(x - r_1(z)\right)\left(x - r_2(z)\right)}
\end{aligned}
\]
同上作代换 \(x = r_1(z)\) 得到 \(z(1 - r_1(z)(1 + r_1(z))z) F(z,0) - r_1(z) = 0\),故 \(f_0(z) = F(z, 0) = \dfrac{r_1(z)}{z(1+z)(1-r_1(z))}\),\(f_\beta(z) = z f_0(z)\),进一步有
\[F(z,x) = \dfrac{r_1(z)(1 + xz r_1(z))}{z(1+z)(1-r_1(z))(1-xr_1(z))}
\]
从这个式子中得到 \(\forall k \ge 1, f_k(z) = \dfrac{r_1^{k + 1}(z)}{z(1 - r_1(z))}\)。作为检验,化简 \(f_\beta(z) + \sum_{m\ge 0} f_i(z)\) 得到 \((1-2z)^{-1}\),这与其组合意义相符。
要对 \(m\ge 1\) 的情况计算 \([z^n x^m] F(z,x)\),使用另类拉格朗日反演,得到
\[[z^n] \dfrac{r_1^{m + 1}(z)}{z(1 - r_1(z))} = [z^{n + 1}] \dfrac{z^{m + 1}}{1-z} (1-z^2) (1 + z^2)^n = [z^{n - m}] (1 + z) (1 + z^2)^n = \binom{n}{\left\lfloor \frac{n-m}{2} \right\rfloor}
\]
由于 \((1 + z^2)^n\) 只有偶数处有值,最后一步讨论了 \(n - m, n - m - 1\) 的奇偶性。此外,我们也可以对任意的 \(n, m\) 计算 \(F\) 的系数,繁而不难,从略。
下一个模型包含大小为 \(1\) 的箱子,以及随机到来的大小为 \(\frac 14,\frac 12, \frac 34\) 的物品。这一次我们能得到两个状态组成的无穷序列,分别表示 \(i\) 个装了 \(\frac 34\) 的箱子,以及 \(i\) 个装了 \(\frac 34\) 的箱子加上一个装了 \(\frac 12\) 的箱子。相关的图如下:
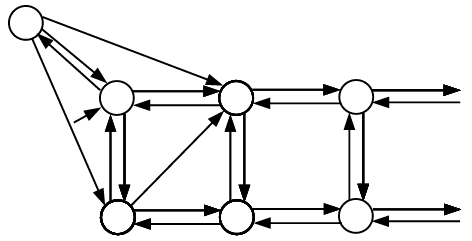
考虑生成函数:\(f_k(z)\) 计数了 \(k\) 个装了 \(\frac 34\) 的箱子的状态,\(g_k(z)\) 计数了 \(k\) 个装了 \(\frac 34\) 的箱子、一个装了 \(\frac 12\) 的箱子的状态,\(h(z)\) 计数了一个装了 \(\frac 14\) 的箱子的状态。据图立得
\[\begin{aligned}
f_{0}(z) & =1+z f_{1}(z)+z g_{0}(z)+z h(z), \\
g_{0}(z) & =z f_{0}(z)+z g_{1}(z)+z h(z), \\
f_{1}(z) & =z f_{0}(z)+z f_{2}(z)+z g_{0}(z)+z g_{1}(z)+z h(z), \\
f_{i}(z) & =z f_{i-1}(z)+z f_{i+1}(z)+z g_{i}(z), \quad i \ge 2, \\
g_{i}(z) & =z g_{i-1}(z)+z g_{i+1}(z)+z f_{i}(z), \quad i \ge 1, \\
h(z) & =z f_{0}(z)
\end{aligned}
\]
令 \(F(z,x) = \sum_{k\ge 0} f_k(z) x^k,G(z,x) = \sum_{k\ge 0} g_k(z) x^k\),有
\[\begin{aligned}
F(z,x) &= 1 + zx F(z,x) + \frac zx \left[F(z,x) - f_0(z)\right] + z G(z,x) + zxg_0(z) + z(1 + x) h(z) \\
G(z,x) &= zF(z,x) + zxG(z,x) + \frac zx \left[G(z,x)-g_0(z)\right] + zh(z)
\end{aligned}
\]
生成函数的形式可能可以直接写出。注意到上面两个式子中 \(F, G\) 的系数是对应的,那么这里设 \(A(z,x) = F(z,x) + G(z,x), B(z,x) = F(z,x) - G(z,x)\),据上得到
\[\begin{aligned}
A(z,x) &= \dfrac{x-z\left[f_0(z) + g_0(z)\right] +zx^2g_0(z) + z^2x(2+x) f_0(z)}{(1-z)x - zx^2 - z} \\
B(z,x) &= \dfrac{x-z\left[f_0(z) + g_0(z)\right] +zx^2g_0(z) + z^2x^2 f_0(z)}{(1+z)x - zx^2 - z}
\end{aligned}
\]
令 \(r_{1,2}(z) = \dfrac{1-z \mp \sqrt{1-2z-3z^2}}{2z}\) 为 \((1-z)x-zx^2 - z = 0\) 的二解,显然 \(-r_{1,2}(-z)\) 为 \((1+z)x-zx^2 - z = 0\) 的二解。又,\(x - r_1(z)\) 和 \(x + r_1(-z)\) 均需要从分母中约去。分别带入 \(x = r_1(z), x = -r_1(-z)\),我们有
\[\begin{aligned}
r_1(z)-z\left[f_0(z) + g_0(z)\right] +zr_1^2(z)g_0(z) + z^2r_1(z)(2+r_1(z)) f_0(z) = 0 \\
-r_1(-z)-z\left[f_0(z) + g_0(z)\right] +zr_1^2(-z)g_0(z) + z^2r_1^2(-z) f_0(z) = 0
\end{aligned}
\]
解得
\[\begin{aligned}
f_{0}(z) & =\frac{r_{1}(z)-r_{1}(-z)+r_{1}^{2}(z) r_{1}(-z)+r_{1}(z) r_{1}^{2}(-z)}{z\left(2-2 z r_{1}(z)-(1+z) r_{1}^{2}(z)+(1-z) r_{1}^{2}(-z)-2 z r_{1}(z) r_{1}^{2}(-z)\right)} \\
g_{0}(z) & =\frac{r_{1}(z)+r_{1}(-z)-2 z r_{1}(z) r_{1}(-z)-z r_{1}^{2}(z) r_{1}(-z)-z r_{1}(z) r_{1}^{2}(-z)}{z\left(2-2 z r_{1}(z)-(1+z) r_{1}^{2}(z)+(1-z) r_{1}^{2}(-z)-2 z r_{1}(z) r_{1}^{2}(-z)\right)}
\end{aligned}
\]
进一步原则上可以解得 \(F(z,x), G(z,x)\) 的表达式,但其实在过于繁琐,不再列出。我们可以用这结果做些事情,例如计算接收 \(n\) 件物品后平均浪费的空间。答案的生成函数即
\[\sum_{k\ge 0} \dfrac{k}{4} f_k(z) + \sum_{k\ge 0} \left(\dfrac{k}{4} + \dfrac 12\right)g_k(z) + \dfrac 34 h(z) = \dfrac{1}{4}\left.\left[\dfrac{\partial}{\partial x}\left(F(z,x) + G(z,x)\right)\right]\right\rvert_{x = 1} + \dfrac{G(z,1)}{2} + \dfrac 34
\]
符号计算可以生成与其等价的表达式。尽管并不好看,但我们还是可以得到在其主导奇点(dominant singularity)\(z = \frac 13\) 周围的展开:
\[\dfrac{\sqrt 3}{12} \left(1 - 3z\right)^{-3/2} + \left( \dfrac{\sqrt 3}{24} + \dfrac 18 \right) \left(1 - 3z\right)^{-1} + \cdots
\]
从中我们可以用生成函数的奇点分析得到平均浪费的空间
\[W_n = \frac 16 \sqrt{\dfrac{3n}{\pi}} + \dfrac{3 + \sqrt 3}{24} + O(n^{-1/2})
\]
如有需要也可以展开更多项。(在 \(z = -\frac 13\) 处也有一个奇点,但其只会贡献阶 \(n^{-1/2}\) 的项)
\(3.\) 卫生纸问题
一个 Knuth 引入的流行主题。考虑两卷卫生纸,分别有 \(m, n\) 张,以及随机的使用者们。每个使用者有 \(p\) 的概率在更大的卷里撕下一张使用,有 \(q = 1 - p\) 的概率使用更小的卷。我们关注的是当小卷卫生纸用完时,大卷卫生纸还剩下的(平均)张数。令 \(m\) 是大卷卫生纸的张数,\(n\) 是小卷的。那么令 \(M_{m,n}\) 为期望剩下的张数,递归如下:
\[\begin{aligned}
M_{m,0} &= m \\
M_{m,m} &= M_{m,m-1}, \quad m \ge 1 \\
M_{m,n} &= p M_{m - 1, n} + q M_{m, n - 1}, \quad m > n > 0
\end{aligned}
\]
上面的二维状态转移都有一个性质:我们可以将各个状态分割成不同的层,转移是在层间进行的,我们可以对层建立生成函数。在这里,我们可以斜着分层,这启发我们首先定义
\[f_0(z) = \sum_{m \ge 0} M_{m,m} z^m, \quad f_1(z) = \sum_{m \ge 1} M_{m,m - 1} z^m
\]
显然 \(f_0 = f_1\)。进一步的,定义
\[F(z,x) = \sum_{m\ge n \ge 0} M_{m,n}z^m x^{m - n}
\]
那么
\[\begin{aligned}
F(z,x) &= \sum_{m > n > 0} M_{m,n} z^m x^{m - n} + \sum_{m\ge 0} M_{m,0}z^m x^m + \sum_{m\ge 0} M_{m,m}z^m
\\ &= \sum_{m > n > 0} \left[p M_{m - 1, n} + q M_{m, n - 1}\right] z^m x^{m - n} + \dfrac{zx}{(1-zx)^2} + f_0(z)
\\ &= pzx \left[F(z,x) - \sum_{m\ge 0} M_{m,0} z^m x^m\right] + \dfrac{q}{x} \left[F(z,x) - x f_1(z) - f_0(z)\right] + \dfrac{zx}{(1-zx)^2} + f_0(z)
\\ &= \left(pzx + \dfrac qx\right) F(z,x) + \dfrac{zx(1-pzx)}{(1-zx)^2} + \left(1 - q - \frac qx\right) f_0(z)
\end{aligned}
\]
自然得到
\[F(z,x) = \dfrac{(q - px) f_0(z) - \frac{zx^2(1-pzx)}{(1-zx)^2}}{pzx^2 - x + q}
\]
同样地,令分母为 \(pz(x - r_1(z))(x - r_2(z))\),其中
\[r_{1,2}(z) = \dfrac{1\mp \sqrt{1-4pqz}}{2pz}
\]
那么同样地,\(x - r_1(z)\) 必为分子的因式,得到
\[(q - pr_1(z)) f_0(z) - \frac{zr_1^2(z)(1-pzr_1(z))}{(1-zr_1(z))^2} = 0
\]
解得
\[f_0(z) = \dfrac{z\left(q - C(pqz)\right)}{q(1-z)^2}, \quad \text{where } C(z) = \dfrac{1 - \sqrt{1 - 4z}}{2}
\]
注意 \(r_1(z) = C(pqz) / pz, 1/r_2(z) = C(pqz) / q\)。这个例子的渐进分析没看懂,不看了。
\(?.\) 总结
虽然原文还有一半,以及五个例子,但我想就此打住,因为上面的例子已经很好地描述了这个方法。
对二元生成函数的处理大致是这样的:通过组合结构推导出一个分式结构,其中分母完全已知,且分子中包含目前无法求得的部分;将分母因式分解,逐个检查因式;由于所求得的函数在 \((0, 0)\) 周围可以展开为幂级数,这个点不能是奇点,若分母的一个因式在 \((0, 0)\) 处收敛到 \(0\),则其也应当是分子的因式,从而解出分子中无法求得的部分。
好像有点感性,但原论文也没有讲分析相关的原因,或者推广。原论文里所有的例子都是分母关于 \(x\) 的度小于等于 \(2\) 的情况,那么直接求根公式套上去解决。至于更复杂的情况……留待后续的博客说吧。