读算法简史：从美索不达米亚到人工智能时代06人工智能现身

1. 人工智能现身

1.1. 在20世纪四五十年代，计算机在本质上被看成一种快速计算器

• 1.1.1. 主机一个接一个地运行大量的数据处理作业(job)，不与用户发生交互

• 1.1.2. 最终的大量打印结果由操作员按批次(batch)展示给他们心怀感激的客户

1.2. 在工业级算术的扩张过程中，个别有远见的人想知道计算机是否能做得更多

• 1.2.1. 计算机从本质上来说是符号操纵机

• 1.2.1.1. 符号可以代表任何信息

• 1.2.2. 如果对这些符号的操纵是正确的，计算机甚至可以执行在此之前必须人类智能才能做的任务

2. 克里斯托弗·斯特雷奇

2.1. 人工智能先驱

2.2. 1916年，斯特雷奇出生于一个富裕的知识分子家庭

• 2.2.1. 毕业于剑桥大学国王学院，获得物理学学位

• 2.2.2. 后来成为牛津大学首位计算机科学教授

• 2.2.3. 于1975年去世，终年58岁

2.3. 自动计算机(Automatic Computing Engine，ACE)

• 2.3.1. ACE原本应该成为英国的第一台通用计算机

• 2.3.2. 一项简单得多的设计——Pilot ACE最终在1950年投入使用

• 2.3.2.1. 大多数初学者是从简单的编程任务开始

2.4. 美国国家研究开发公司(National Research and Development Corporation，NRDC)

• 2.4.1. NRDC的职责是将政府部门的新技术转让给私营机构

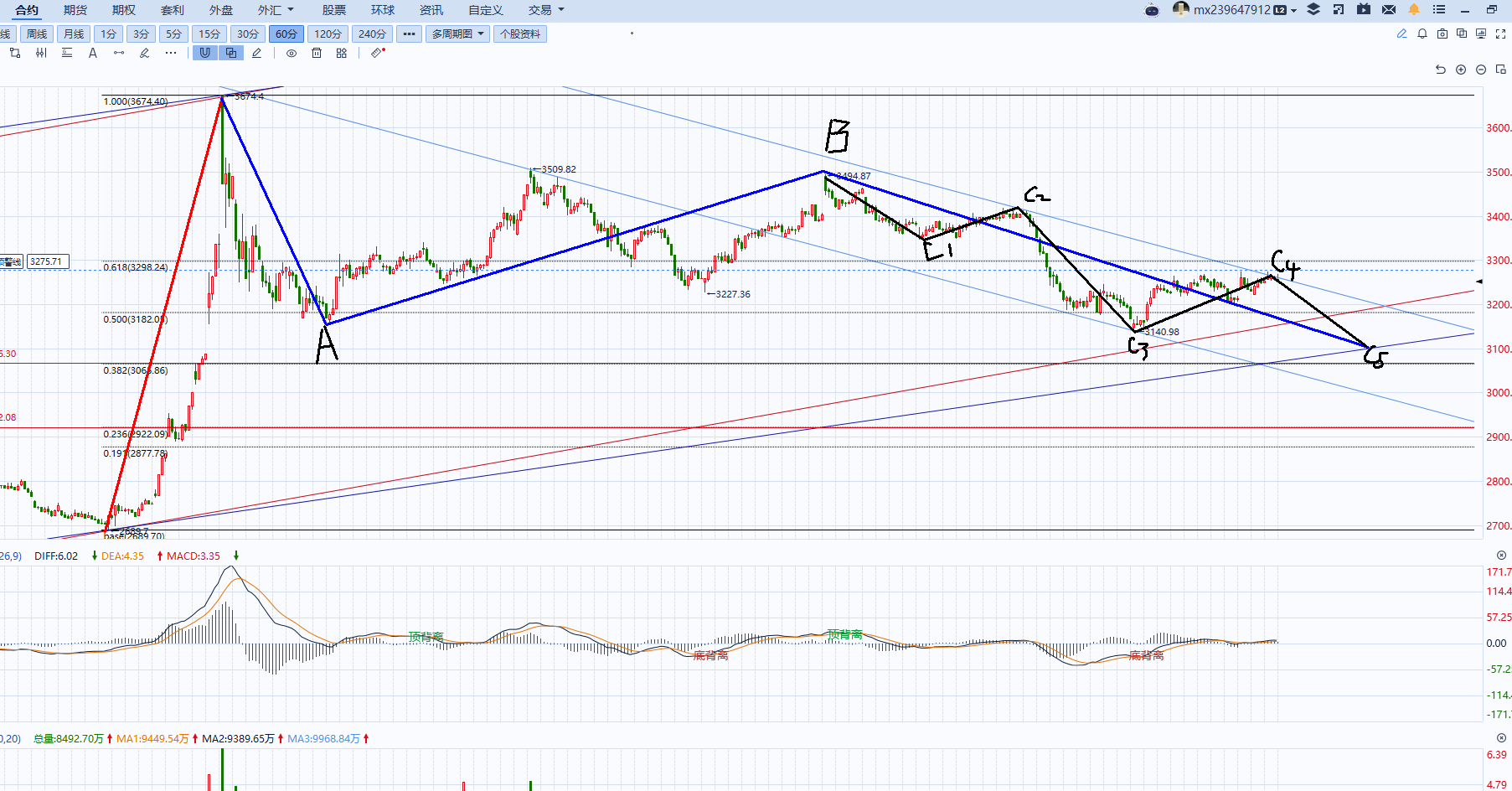
2.5. 斯特雷奇最终在1952年完成了他的国际跳棋程序，并在一篇题为《逻辑或非数学程序》(Logical or Non-Mathematical Programmes)的论文中描述了它

• 2.5.1. 游戏的目标是清除对手所有的棋子

• 2.5.2. 斯特雷奇的算法用数字来记录棋局

• 2.5.3. 轮到己方走棋时，算法会计算所有可能的下一步棋（走法平均有10种）

• 2.5.4. 一个回合(move)包含两次走棋，每个玩家各走一次

• 2.5.5. 单次走棋（或称半个回合）被称为一步(ply)

• 2.5.6. 对于下一回合的每一种可能，算法都会评估对手的潜在应对方式

• 2.5.7. 每一个棋局都是树上的一个节点(node)，或称为分支点

• 2.5.8. 前瞻预测的范围越大，树中的层就越多

• 2.5.8.1. 对于前瞻预测结束时的节点，算法会计算每个玩家在棋盘上得以留存的棋子的数量

• 2.5.8.2. 它以树的根部为起点，选择最优走法，该走法能为计算机在前瞻预测结束时带来最大的数值优势

2.6. 事后看来，该程序的前瞻预测深度不足，决策逻辑缺乏复杂性，对棋局的评估也不准确

• 2.6.1. 计算机只用来制霸算术的局面已经被打破了

• 2.6.2. 这是人工智能(artifi cial intelligence，AI)的第一个实例

2.7. 玩国际跳棋需要逻辑推理和预见能力

• 2.7.1. 斯特雷奇的成果就从手写的笔记转变成了一个可以运行的千行程序

• 2.7.1.1. 这个程序解出了图灵设定的问题，并在完成后用计算机音响播放了英国国歌

• 2.7.1.2. 这是由计算机播放出的第一首音乐

2.8. 尽管斯特雷奇是一位颇受尊敬的学者，但由于他对发表学术论文并不积极，他后来的许多工作并未得到认可

3. AI的麻烦

3.1. 1955年，约翰·麦卡锡(John McCarthy)在向洛克菲勒基金会提交的一份提案中创造了“人工智能”一词

3.2. 大多数人会认同执行一个算法不需要智能

• 3.2.1. 当下棋的算法未知时，玩跳棋需要智能

• 3.2.2. 一旦知道了跳棋的算法，玩跳棋就不再需要智能了

3.3. 麦卡锡所定义的人工智能一直是未能解答的难题

• 3.3.1. 一旦算法被知晓，解决这个问题就不再需要智能了

• 3.3.2. 我们感觉智能应该是用来解决计算机无法解决的智力任务的

• 3.3.3. 在某些方面，人工智能类似于舞台魔术

• 3.3.3.1. 一旦我们知道魔术是如何做到的，它就不再是魔术了

3.4. 人类的智能是多方面且通用的，意思是我们的智能有很多方面的体现

• 3.4.1. 我们可以学习、回忆、多任务并行、发明、应用专业知识、想象、感知、抽象等

• 3.4.2. 人类的智能是通用的，因为我们可以执行各种各样的任务

3.5. 与人类智能类似的那种智能，其恰当的术语是“人类级别的人工通用智能”(human-level artifi cial general intelligence，HLAGI)

• 3.5.1. AI是一个科学事实，与HLAGI相去甚远

3.6. 麦卡锡AI定义的一个重要方面是，他从输出结果的角度来描述AI

• 3.6.1. 只要机器产出了比得上人类的结果，那么他就认为人工智能达到了人类智能的水平

3.7. 如果有外星人来到地球，我们会仅仅因为它们是硅基生命，而非碳基生命就认为它们不能思考吗

• 3.7.1. 思考的先决条件是智能加上意识

• 3.7.2. 意识，即具有能自我感知的状态，允许有知觉的生物能“听到”自己在“思考”

• 3.7.3. 对于图灵来说，如果机器的行为与人类的智能无法进行区分，那么我们就可以得出结论说机器能“思考”​

3.8. 机器是否“有感觉”这一点意义重大

• 3.8.1. 如果机器有意识和情感，那么毫无疑问，我们对它负有道德责任

• 3.8.2. 随着技术的进步，这样的问题会越来越重要

4. 艾伦·纽厄尔和赫伯特·西蒙与机器推理

4.1. 代数是研究包含未知值方程的数学分支

• 4.1.1. 几千年来，操纵方程都是数学家的工作

• 4.1.2. 这是算盘、计算器和早期计算机程序无法做到的

4.2. 兰德公司

• 4.2.1. 在20世纪50年代，兰德公司的头号客户是美国空军

• 4.2.2. 兰德公司是研究人员的天堂：学术自由、聪明的同事、充裕的预算、不需要教学

• 4.2.3. 兰德公司的计算机JOHNNIAC是基于IAS蓝图搭建的

4.3. 两名美国科学家艾伦·纽厄尔(Allen Newell)和赫伯特·西蒙(Herbert Simon)公布了一种可以执行代数运算的计算机程序

• 4.3.1. 通过代数的方法，可以对这样的方程进行操作，从而体现变量之间新的关系

• 4.3.2. 从一组初始方程得出结论的一系列运算称为证明(proof)

• 4.3.3. 其思想是，如果初始方程组是有效的，并且运算法则应用得当，那么结论也必然是有效的

• 4.3.4. 开始的方程称为前提(premise)，最后的结论称为推论(deduction)

• 4.3.5. 程序回溯并输出连接推论到初始前提的那个方程转换链，将转换链作为证据呈现给用户

4.4. 开发了一个名为“逻辑理论家”的人工智能程序

• 4.4.1. 由于CIT没有计算机，两人在教室里召集了一组学生，让他们模拟计算机的行为，以此来测试他们的程序

• 4.4.2. 1955年12月15日，该团队宣布“逻辑理论家”可以运行

• 4.4.3. 逻辑理论家”为经典教材《数学原理》(Principia Mathe-matica)中52个定理中的38个提供了一步一步的证明

• 4.4.3.1. ​“逻辑理论家”的其中一个证明比教科书版本的更为优雅

4.5. 1959年，纽厄尔、肖和西蒙推出了一项新计划：​“通用问题求解者”

• 4.5.1. “通用问题求解者”算法并不会尝试所有可能的操作

• 4.5.2. 它对与期望推论相似的方程进行优先处理

• 4.5.2.1. 这意味着它在探索无用的路径上花费的时间更少

• 4.5.2.2. 由于速度快，规则引导搜索或者说启发式搜索(heuristic search)目前被广泛使用

• 4.5.3. “通用问题求解者”模仿了人类的推理过程

• 4.5.3.1. 人类有时通过试错得出正式的数学证明的方式与此确有相似之处

• 4.5.3.2. 人类的推理似乎比“通用问题求解者”的推理方式更直觉化，也更不严谨

4.6. 人工智能的一整个子领域（符号推理，symbolic reasoning）都起源于将逻辑语句处理为符号列表的概念

4.7. 1967年，CIT与梅隆学院合并，成立了卡内基梅隆大学(Carnegie Mellon University，CMU)

• 4.7.1. 纽厄尔和西蒙随后在CMU建立了世界领先水平的人工智能研究小组

• 4.7.2. 1975年，他们因在AI和认知心理学方面的工作被授予图灵奖

• 4.7.3. 3年后，西蒙因在微观经济学领域的贡献获得了诺贝尔奖，这是他的另一个研究兴趣所在

4.8. 纽厄尔于1992年去世，享年65岁

4.9. 西蒙于2001年去世，享年84岁

5. 亚瑟·塞缪尔与机器学习

5.1. 学习能力是人类智能的核心

• 5.1.1. 学习能力是人类智能的核心

• 5.1.2. 孩子通过模仿大人和反复试错来学习走路

5.2. 1956年2月24日，第一个用来展示学习能力的计算机程序在公共电视节目上公布

• 5.2.1. 这个程序是由IBM的亚瑟·塞缪尔(Arthur Samuel)编写的

• 5.2.2. 塞缪尔的程序和斯特雷奇的一样，也是玩国际跳棋

• 5.2.3. 电视演示给人们留下了深刻的印象，IBM的股价在第二天上涨了15个点

5.3. 1959年，塞缪尔终于发表了一篇论文，描述他的新国际跳棋程序

• 5.3.1. 这篇文章的低调标题——《利用跳棋游戏进行机器学习的一些研究》(Some Studies in Machine Learning using the Game of Checkers)——掩盖了其思想的重要性

• 5.3.2. 塞缪尔的算法比斯特雷奇的算法更为全面

• 5.3.3. 它通过一种巧妙的评分算法来实现这一点

• 5.3.3.1. 算法对各种会用到的特征(feature)进行打分

• 5.3.3.2. 特征是指任何表明一个棋局的长处或弱点的东西

• 5.3.3.3. 其中一个特征是两个对手棋盘上棋子数量的差异

• 5.3.3.4. 权重决定了每个特征的相对重要性

>  5.3.3.4.1. 负权重意味着该特征降低了计算机获胜的可能性>  5.3.3.4.2. 权重越大，说明某一特征对总分的影响力越大

5.4. 塞缪尔的棋局评价方法工作原理

• 5.4.1. 以一个棋局作为输入

• 5.4.2. 将总分设置为零

• 5.4.3. 对每个特征重复以下步骤

• 5.4.3.1. 测量棋盘上的某个特征

• 5.4.3.2. 计算该特征的得分

• 5.4.3.3. 乘以特征的权重

• 5.4.3.4. 把计算结果加到总分中

• 5.4.3.5. 当所有特征都评分完成后，停止重复

• 5.4.4. 输出总分

5.5. 随着游戏的进行，算法会调整权重，以便计算出的分数能更准确地预测游戏的结局

• 5.5.1. 任何起到负面作用的权重都将降低

• 5.5.1.1. 这强化(reinforce)了获胜行为

5.6. 与人工选择权重相比，塞缪尔的算法具有两方面的优势

• 5.6.1. 计算机永远不会忘记

• 5.6.1.1. 每一步棋都会影响到权重

• 5.6.2. 计算机可以与自己进行多次游戏，远远超过人类能玩的次数

• 5.6.3. 在学习过程当中可以获得更多的信息

5.7. 塞缪尔对机器学习的开发是颠覆性的

• 5.7.1. 塞缪尔的程序所做的决策是由权重控制的，权重是简单的数值

• 5.7.2. 程序的行为可以通过改变权重来调整

• 5.7.3. 程序代码不需要修改

• 5.7.4. 更改程序代码很困难，但更改几个权重数值是很容易的

5.8. 塞缪尔还加入了一个极小化极大(minimax)步骤来选择走法

• 5.8.1. 在真实的游戏中，不太可能出现一些最高得分的棋局，因为它们是由对手特别糟糕的表现造成的

• 5.8.2. 轮到自己走棋时，回溯算法会选择能够获得最高得分的走法

5.9. 极小化极大步骤

• 5.9.1. 以可能走法的树作为输入

• 5.9.2. 从倒数第二个层级开始

• 5.9.3. 对每一层级重复以下步骤

• 5.9.3.1. 对该层级的每个节点重复如下操作

>  5.9.3.1.1. 如果轮到计算机走棋，那么就选择得分最高的走法，否则选择得分最低的走法>  5.9.3.1.2. 将极小化极大得分值复制到当前节点>  5.9.3.1.3. 检查完这一层级中的所有节点后，停止重复

• 5.9.3.2. 当到达树的根部时停止重复

• 5.9.4. 输出具有最大回溯分数的走法

5.10. 为了高效利用可用的计算时间，塞缪尔的程序会根据一组规则（使用启发式搜索）调整前瞻预测的深度和宽

• 5.10.1. 对解题过程进行剪枝(pruning)，可以为评估更可能出现的场景让出更多的时间

• 5.10.2. 为了进一步加快处理速度，塞缪尔的程序存储了常见棋局的极小化极大分数

• 5.10.2.1. 这些分数不需要在程序运行期间重新计算，因为单纯从表里查找就足够了

5.11. 1966年，塞缪尔从IBM退休，进入斯坦福大学担任研究教授职位

• 5.11.1. 在85岁高龄时仍在编程，但帕金森病最终迫使他停止工作

• 5.11.2. 塞缪尔于1990年去世

5.12. 当今世界最先进的棋盘游戏算法的雏形可以在塞缪尔20世纪50年代的工作中找到

• 5.12.1. 极小化极大、强化学习和自对弈几乎是所有现代国际跳棋、国际象棋和围棋AI的基础

• 5.12.2. 在很多应用中，机器学习已被证明在处理复杂的数据分析问题时极其有效

6. AI寒冬

6.1. 为什么那么多杰出的思想家都大错特错了？

• 6.1.1. 预测没有一个成真

• 6.1.2. 最简单的答案就是傲慢

• 6.1.3. 这些人都是数学家。对他们来说，数学是智能的巅峰

• 6.1.4. 他们没有认识到现实世界的可变性和人类大脑的复杂性

• 6.1.5. 事实证明，处理图像、声音和语言比处理方程式要复杂得多

6.2. 考虑到计算机性能的局限性，一些科学家尝试开发快速算法来解决重要但需要复杂计算的问题