被迫卷入了一场决定一切的 Nim 游戏。
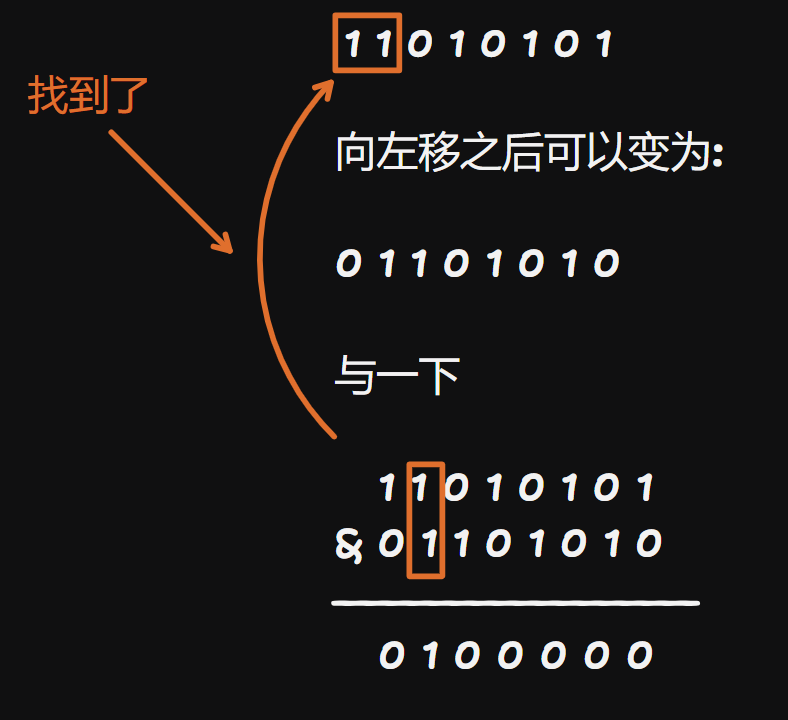
先简化操作:我们每一次可以选择一个数将其第 \(i\) 位从 \(0\) 变成 \(1\),更低位清零。
下面成一个数做上面的那个事情为“执行操作”。
考虑从高位到低位操作。每次选择一些数执行操作,使得这一位的异或和变成零。因为对一位操作不会影响更高位,所以这样顺序做是对的。
设第 \(i\) 位对 \(len_i\) 个数执行了操作。
贪心结论: \(a_1 = 0\) 时,\(len_i\) 一定小于 \(1\)。
\(a_1 = 0\) 是特殊性质 B。这时不会出现 \(n\) 为奇数且这一位全为 \(1\),使我们无法操作的情况。这种情况后面再看(
上面结论证明:这一位为偶数时,不妨选 \(len_i = 2\),若选了 \(x,y\) 两个数,代价为 \(2^{i+1} - x - y\),对后面的影响为 \(x \oplus y\)。相当于我们在后面用 \(x \oplus y\) 的代价可以达到相同的效果。显然 \(x + y + x \oplus y \le 2 \times 2^{i-1} < 2^{i+1}\)(对每一位考虑,\(x \oplus y\) 的第 \(i\) 位为 \(1\) 时,\(x,y\) 第 \(i\) 位一定不全为 \(1\)),所以一定不优。
这一位为奇数时,一定要选一个数执行操作。后面就是偶数的情况。不会多选了。
用上面的结论可以暴搜或 DP,获得一些分数。
贪心结论: \(len_i = 1\) 时,选择更低位更大的数一定不劣。
这是我考场上没有意识到的。证明非常简单。如果选小的数更优,将大的数执行操作,然后把小的数增加到大的数,也能有同样的效果。
这样每一轮要执行操作时我们都对这一位排序,选出其中更低 \(i-1\) 位中最大的那个数就行了。可以 \(O(n \log n \log V)\) 算出 B 性质的答案。
搜方案需要精细实现。DFS。按后 \(i-1\) 位从大到小排序,每次方案满 \(m\) 个了或者说搜到错误答案就立即返回即可。可以获得 \(72pts\)。
贪心结论: 当一位全是 \(1\) 且 \(n\) 为奇数时,会在一个更高位进行 \(len_i = 2\) 的操作。其他位不变。
首先一定要有一位进行了 \(len_i = 2\) 的操作。所以一定是正确的。且进行操作后,更低位都不会有上述全 \(1\) 的问题了。枚举哪一位进行了该操作即可。根据实现复杂度带 \(2\) 到 \(3\) 只 \(\log\)。