该部分主要通过对比Torch和Numpy基础知识,方便大家了解PyTorch。Numpy是处理数据的模块,处理各种矩阵的形式来多核加速运算。
Torch自称为神经网络界的Numpy,因为它能将torch产生的tensor(张量)放在 GPU 中加速运算(前提是你有合适的 GPU),就像Numpy会把array放在CPU中加速运算。所以神经网络的话,当然是用Torch的tensor形式数据最好,就像Tensorflow当中的tensor一样。
当然,我们对Numpy还是爱不释手的,因为我们太习惯numpy的形式了。不过torch看出来我们的喜爱,他把torch做的和numpy能很好的兼容。
下面来看如何自由地转换numpy array和torch tensor。
import torch
import numpy as np#定义
np_data = np.arange(6).reshape((2,3))
torch_data = torch.from_numpy(np_data)
print("numpy:\n", np_data)
print("torch:\n", torch_data)tensor2array = torch_data.numpy()
print("tensor2array:\n", tensor2array, "\n")
其运行结果如下所示:

接着介绍PyTorch的各种运算符号。
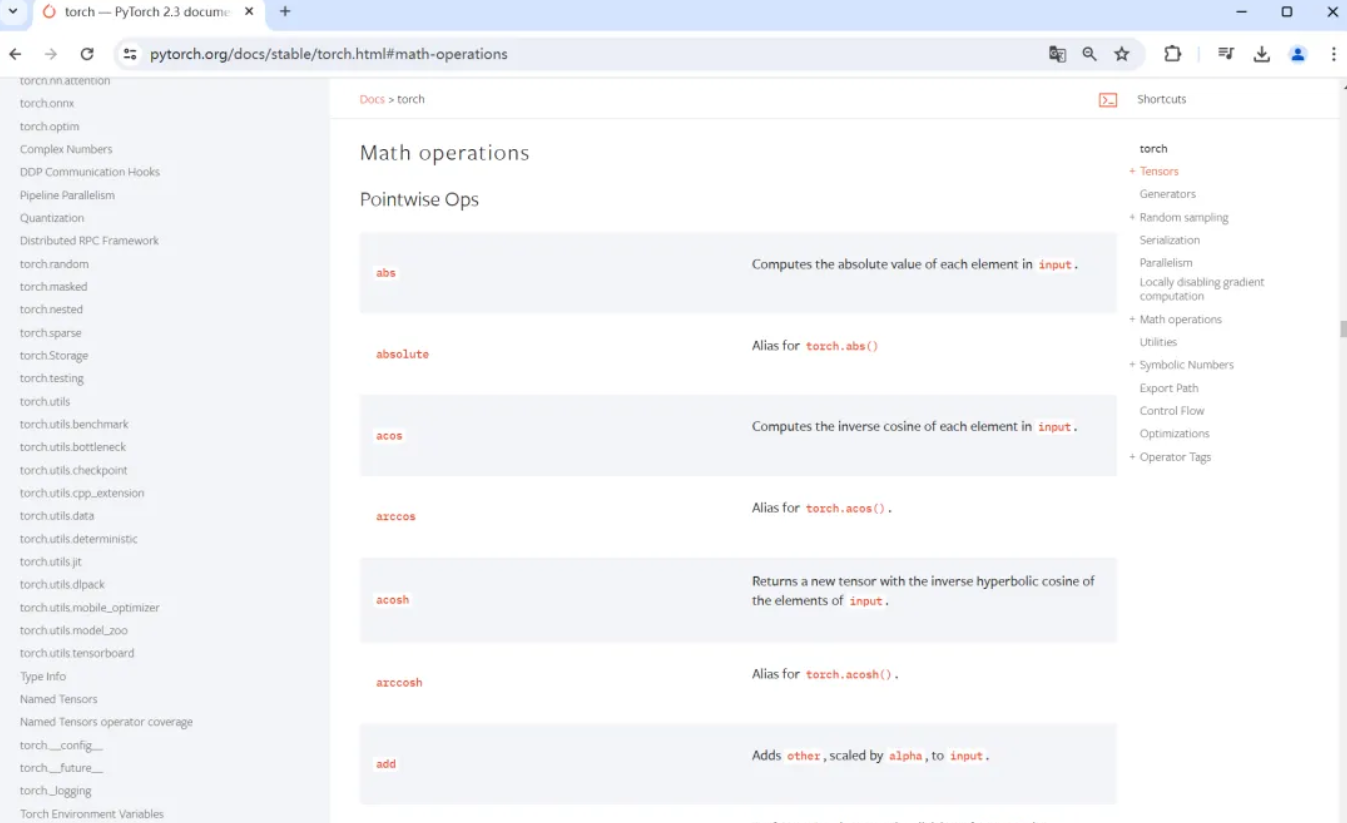
可以通过如下网站看到各种运算符号,方便大家学习。
https://pytorch.org/docs/stable/torch.html#math-operations
import torch
import numpy as np#abs
data = [-1, -2, 1, 2]
tensor = torch.FloatTensor(data) #32bit
print("numpy:", np.abs(data)) #[1 2 1 2]
print("torch:", torch.abs(tensor)) #[1 2 1 2]print("numpy:", np.sin(data))
print("torch:", torch.sin(tensor))print("numpy:", np.mean(data))
print("torch:", torch.mean(tensor), "\n")
运算结果如下所示:

最后介绍矩阵运算。矩阵相乘在Numpy中可以使用np.matmul和dot实现,但Torch的dot会将矩阵展平,其输出结果为9。
import torch
import numpy as np#矩阵
data = [[1,2], [3,4]]
tensor = torch.FloatTensor(data) #32bit floating point
data = np.array(data)
print("numpy:", data.dot(data))
print("torch:", torch.mm(tensor, tensor))A = torch.tensor([1, 1, 1])
B = torch.tensor([2, 3, 4])
print("torch:", torch.dot(A, B))
print("torch:", torch.mul(A, B))
输出结果如下图所示:

注意:pytorch0.3之后,tensor.dot()方法进行了更新,只能对1维的tensor进行点成运算
矩阵计算如下所示:
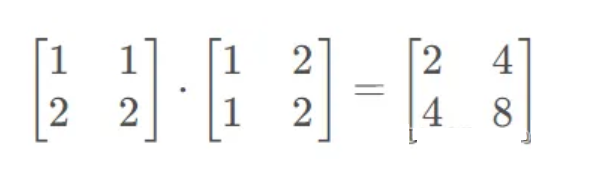
在深度学习中,我们通常需要训练一个模型来最小化损失函数。这个过程可以通过梯度下降等优化算法来实现。梯度是函数在某一点上的变化率,可以告诉我们如何调整模型的参数以使损失函数最小化。自动求导是一种计算梯度的技术,它允许我们在定义模型时不需要手动推导梯度计算公式。PyTorch 提供了自动求导的功能,使得梯度的计算变得非常简单和高效。
下面给出一段示例代码:
import torch# 创建一个变量
x = torch.tensor(1., requires_grad=True)# 执行一些操作
y = x ** 2# 反向传播
y.backward()# 输出结果
print(x.grad) # 输出x相对于自身的梯度,即2*x
在这个例子中,我们首先创建了一个变量x,并设置了requires_grad=True以启用自动求导。然后我们计算了x的平方y,接着调用backward()方法进行反向传播,这将自动计算y相对于创建时所用操作(这里是乘法操作)的梯度,并将梯度结果存储在x.grad中。