基础实验:训练温度传感器数据预测模型
任务描述:LM35是科创作品制作中常用的温度传感器(1)已知电压值,
如何得出实际温度值?(2)输出电压(Sensor)和真实温度(Temperature)有什么关
系?
请借助大模型生成这两列数据的关系图
/目录
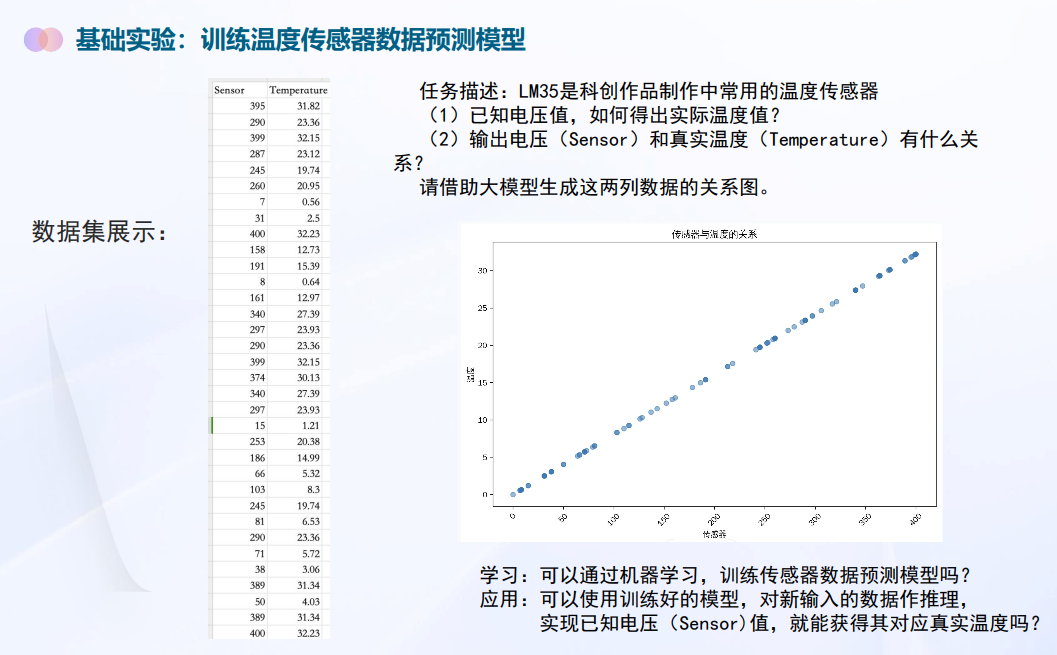
学习:可以通过机器学习,训练传感器数据预测模型吗?应用:可以使用训练好的模型,
对新输入的数据作推理,实现已知电压(Sensor)值,就能获得其对应真实温度吗?

回归任务是预测连续值的任务。
例如,根据房屋面积、房屋年龄等特征预测房屋价格;根据学生的平时成绩、
学习时间等特征预测学生的期末分数;根据上一年的产量、天气和农场员工数等属性来预测下一年玉米农场的产量。
回归任务可以被分为线性回归和非线性回归两种。线性回归是假设输入特征和目标变量之间存在线性关系的回归任务,
而非线性回归是假设输入特征和目标变量之间存在非线性关系的回归任务。
1. 概念
-
回归任务:泛指所有用于预测连续数值输出的任务。它不局限于任何特定的模型,只要目标是预测一个连续的数值,都可以称为回归任务。
-
线性回归:是一种具体的回归模型,假设输入特征与输出目标之间存在线性关系。它通过建立一个线性方程来预测目标值。
2. 模型形式
-
回归任务:可以使用多种模型,包括线性回归、非线性回归、决策树回归、支持向量机回归等。
-
线性回归:模型形式为 y=β0+β1x1+β2x2+⋯+βnxn+ϵ,其中 y 是预测值,xi 是输入特征,βi 是模型参数,ϵ 是误差项。
3. 假设条件
-
回归任务:不同的回归模型有不同的假设条件。例如,线性回归假设特征与目标之间存在线性关系,而非线性回归则可以处理更复杂的关系。
-
线性回归:假设输入特征与输出目标之间存在线性关系,并且误差项服从独立同分布的正态分布。
4. 应用场景
-
回归任务:适用于所有需要预测连续数值的场景,如房价预测、温度预测、销售量预测等。
-
线性回归:适用于数据之间存在明显线性关系的场景,例如根据房屋面积和位置预测房价。
5. 模型复杂度
-
回归任务:可以根据任务的复杂性选择不同的模型。例如,对于简单的线性关系可以使用线性回归,对于复杂的非线性关系可以使用多项式回归或神经网络。
-
线性回归:模型相对简单,计算效率高,但只能处理线性关系,对非线性关系的拟合效果较差。
6. 损失函数
-
回归任务:常用的损失函数包括均方误差(MSE)、平均绝对误差(MAE)等。
-
线性回归:通常使用均方误差(MSE)作为损失函数,通过最小化预测值与真实值之间的平方差来优化模型参数。
总结
回归(Regression)的含义及由来
-
回归的含义
-
从统计学角度:回归是一种统计方法,用于研究一个或多个自变量(特征)与因变量(目标)之间的关系。其目的是通过建立一个数学模型,根据自变量的值来预测因变量的值。例如,预测房价(因变量)与房屋面积、位置、房间数量等特征(自变量)之间的关系。
-
从机器学习角度:回归任务是机器学习中的一个核心任务,目标是预测一个连续的数值输出。与分类任务(预测离散的类别)不同,回归任务的输出是连续的,如预测温度、房价、销售额等。
-
-
回归名称的由来
-
历史背景:回归一词最早由英国生物学家和统计学家弗朗西斯·高尔顿(Francis Galton)在19世纪末提出。他在研究父母身高与子女身高之间的关系时发现,子女的身高趋向于回归到人群的平均身高,即“回归到中庸”(regression to the mean)。他将这种现象称为“回归”。
-
数学背景:在高尔顿的研究中,他通过建立数学模型来描述这种“回归”现象,即子女的身高与父母身高之间的关系。这种模型后来被发展为线性回归模型,成为回归分析的基础。
-
线性关系(Linear Relationship)的含义及理解
-
线性关系的定义
-
数学定义:线性关系是指两个变量之间的关系可以用一条直线来表示。如果变量 y 与变量 x 之间存在线性关系,可以表示为 y=ax+b,其中 a 是斜率,表示 x 每变化一个单位时 y 的变化量;b 是截距,表示当 x=0 时 y 的值。
-
几何意义:在二维平面上,线性关系表示为一条直线。如果在三维空间中,线性关系可以表示为一个平面。
-
-
如何理解线性
-
简单直观的理解:线性关系意味着变量之间的变化是均匀的、成比例的。例如,如果 y 与 x 成线性关系,当 x 增加1个单位时,y 会增加一个固定的量(斜率 a)。这种关系可以用一条直线来描述。
-
多变量情况:在多变量的情况下,线性关系可以表示为 y=a1x1+a2x2+⋯+anxn+b,其中 x1,x2,…,xn 是自变量,a1,a2,…,an 是对应的系数,b 是截距。这种关系可以用一个超平面来表示。
-
与非线性关系的对比:非线性关系则意味着变量之间的变化不是均匀的、成比例的。例如,y=x2 或 y=ex 都是非线性关系,因为它们的变化率不是固定的。
-
总结
-
回归:是一种统计和机器学习方法,用于研究变量之间的关系并预测连续的数值输出。名称来源于高尔顿对“回归到中庸”现象的研究。
-
线性关系:是一种简单的、均匀变化的关系,可以用一条直线或超平面来表示。它是最基本的数学关系之一,也是线性回归模型的基础。
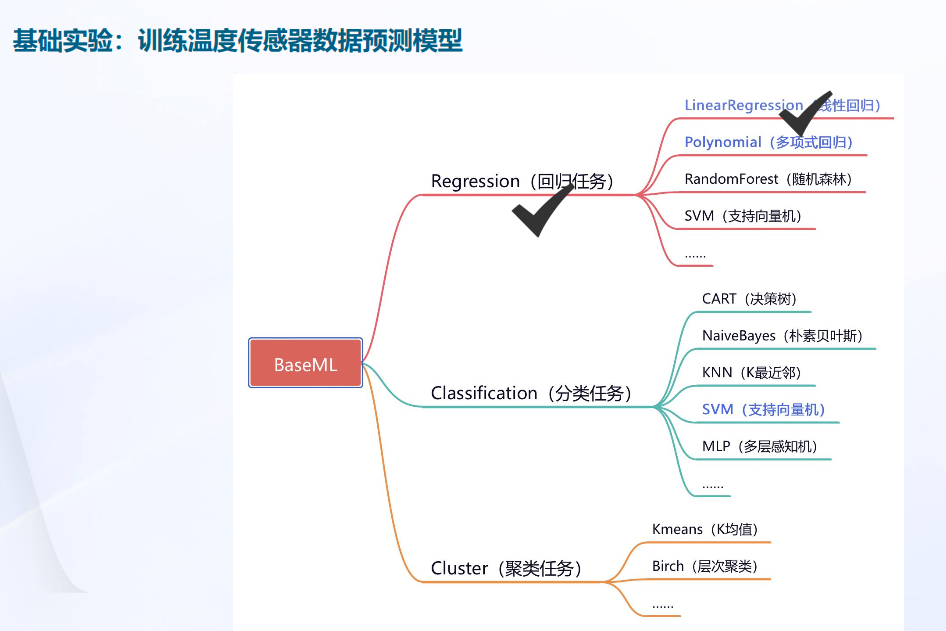
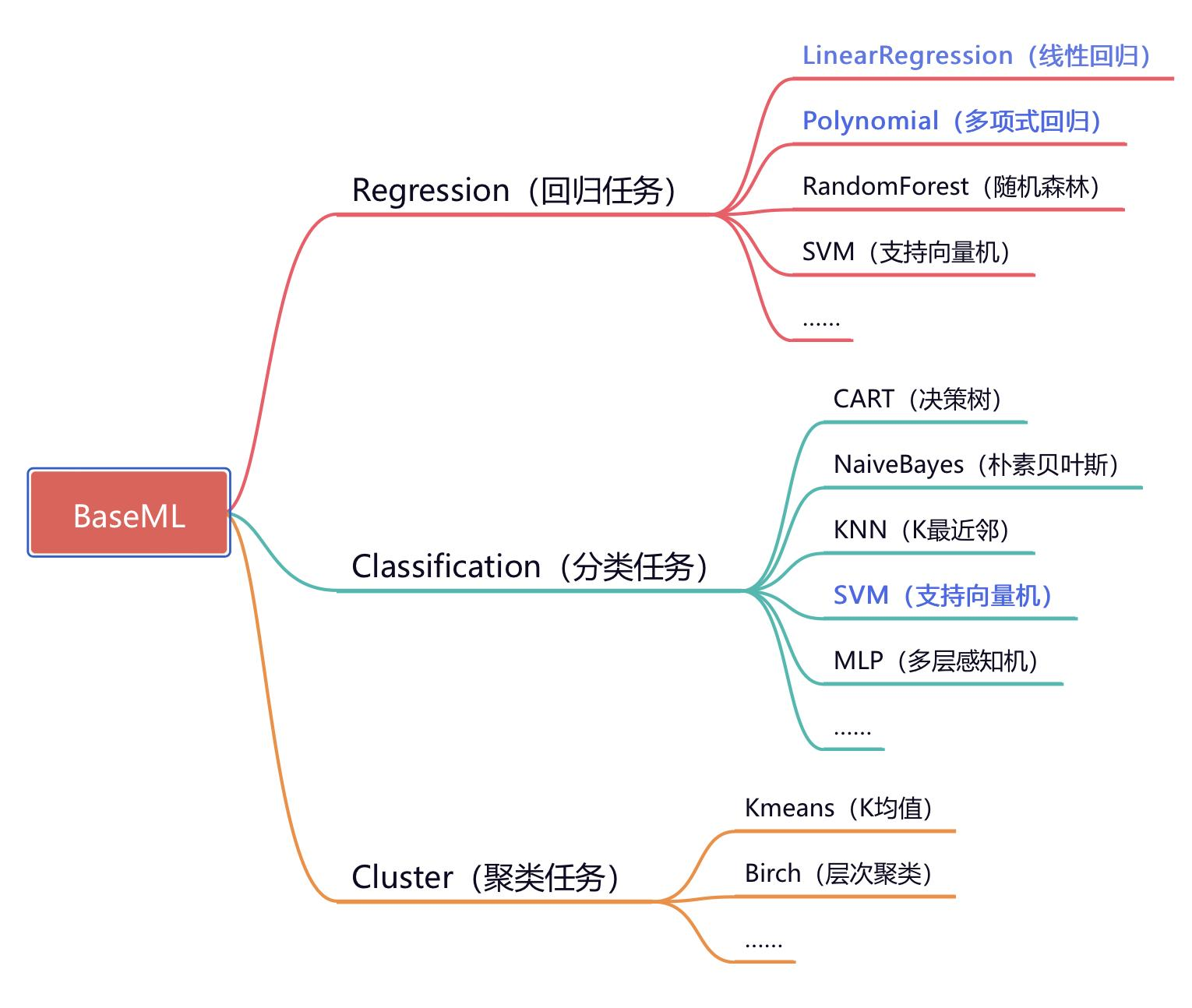

基础实验:训练温度传感器数据预测模型
在准备训练前,先完成数据集划分,即将数据集拆分为训练集和验证集,训练集用于训练模型,验证集用于评估模型的性能
此步骤可以手动完成,也可以用代码完成:借助XEdu的数据处理库BaseDT,指定csv文件路径以及划分比例,将特征数据集划分为训练集(makesensor_train.csv)和验证集(make sensor val.csv)。

步骤1:数据准备(选做)
实验需要用到的数据集在data下面的make_sensor.csv中。这些数据是LM35传感器的测量结果(DFRobot的LM35传感器和行空板),可以将它下载下来看一下具体数据。
步骤2:借助BaseDT划分数据集
在准备训练前,先完成数据集划分,即将数据集拆分为训练集和验证集,训练集用于训练模型,验证集用于评估模型的性能。此步骤可以手动完成,也可以用代码完成:借助XEdu的数据处理库BaseDT,指定csv文件路径以及划分比例,将特征数据集划分为训练集(make_sensor_train.csv)和验证集(make_sensor_val.csv)。
# 更新库文件 !pip install --upgrade BaseDT from BaseDT.dataset import split_tab_dataset # 指定待拆分的csv数据集 path = "data/make_sensor.csv" # 指定特征数据列、标签列、训练集比重 tx,ty,val_x,val_y = split_tab_dataset(path,data_column=range(0,1),label_column=1,train_val_ratio=0.8)

步骤3:加载模型
首先我们需要导入必要的库文件并构建线性回归模型。LinearRegression用于线性回归,它可以帮助我们建立和分析线性模型,从而预测变量之间的关系。
步骤4:训练模型
将数据集载入模型,进行模型训练,并将模型保存至指定路径。
# 导入库文件,选择回归模块
from BaseML import Regression as reg
# 构建线性回归模型
model = reg(algorithm = 'LinearRegression')
# 从data/sensor_train.csv路径载入数据集
model.load_tab_data('data/make_sensor_train.csv')
# 训练模型
model.train()
# 将模型保存至checkpoints/sensor.pkl
model.save('checkpoints/sensor.pkl')

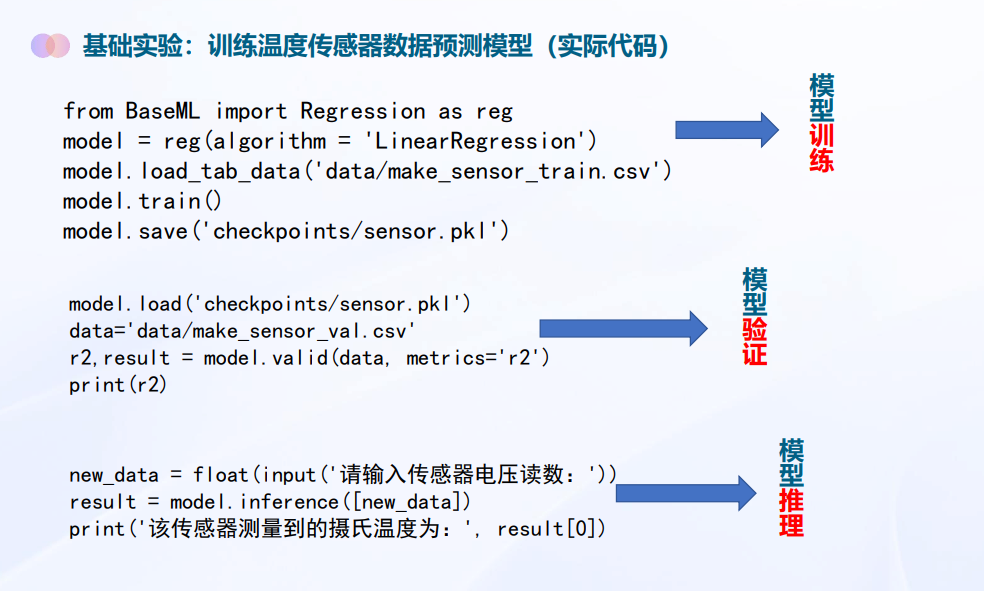
步骤4:验证模型
模型训练完成,但是该模型效果如何?R的平方值可以评价回归模型的准确度。因此,我们可以根据以下的代码进行模型验证。
model.load('checkpoints/sensor.pkl')
data='data/make_sensor_val.csv'
# 读取验证集进行验证并计算R平方值
r2,result = model.valid(data, metrics='r2') # 载入验证数据
# 输出评估指标计算结果
print(r2)

步骤5:应用模型
模型验证后我们就可以应用模型啦。输入模拟引脚数值,测试输出的摄氏温度是否正确。
new_data = float(input('请输入传感器电压读数:'))
result = model.inference([new_data])
print('该传感器测量到的摄氏温度为:', result[0])