前言
Manacher 算法是最好写的字符串算法。——教练
暴力求法
给出一个只由小写英文字符 \(\texttt a,\texttt b,\texttt c,\ldots\texttt y,\texttt z\) 组成的字符串 \(S\),求 \(S\) 中最长回文串的长度 。
暴力算法 \(1\):
枚举左右端点,\(O(n)\) 判断是否为回文串,时间复杂度 \(O(n^3)\)。
暴力算法 \(2\):
枚举中间点(包括字符与字符之间的空隙),根据回文串的性质,向左右两边扩展。如果左右并不相等,立即结束并更新答案;否则将左右各推一个字符,当前答案自增。时间复杂度 \(O(n^2)\)。
但是,此题的数据范围是 \(1\le |S|\le 1.1\times 10^7\)。
Manacher 算法
预处理
Manacher 算法是基于暴力算法 \(2\) 的再优化,由于回文串的对称中心有可能会在两个字符之间的空隙处,所以我们可以插入一些特殊字符,例如 #。为了避免越界,我在字符串开头也插入了一个特殊字符 !。
下标从 \(1\) 开始。
由于格式影响,代码中与 \(\LaTeX\) 公式相冲突的字符改为了 !。
scanf("%s",stri);
int l=strlen(stri);
str[0]='!';
for(int i=0;i<l;i++){str[i*2+1]='#';str[i*2+2]=stri[i];}
str[l*2+1]='#';
l=l*2+1;
最长回文延伸长度
以 \(i\) 为中心的最长回文延伸长度,记作 \(p[i]\)。
例如,字符串 abaaabaa 的 p 数组:
| a | b | a | a | a | a | b | a | a | |
|---|---|---|---|---|---|---|---|---|---|
| \(p[i]\) | \(1\) | \(2\) | \(1\) | \(2\) | \(2\) | \(1\) | \(3\) | \(1\) | \(1\) |
注意一个字符也算回文串,所以 \(p[i]\) 的最小值为 \(1\)。
可以知道,对于每个位置 \(i\),以 \(i\) 为中心的最长回文串的起始位置为 \(i-p[i]+1\),结束位置为 \(i+p[i]-1\)。
算法流程
由于回文串在回文中心左右的部分完全对称,我们可以考虑从这一点来优化算法,进行递推。Manacher 算法的递推方向就是从左到右。(下标从 \(1\) 开始)
\(1\):最理想的情况
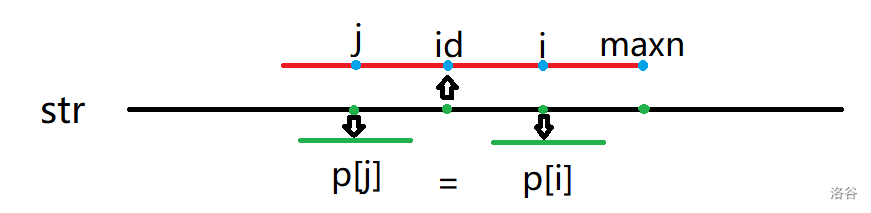
(自绘插图,略显粗糙)
如图,\(maxn\) 表示目前求出的回文串中最远延伸的点,而 \(id\) 表示这个字符串的对称中心。点 \(i\) 是我们正在求的点,点 \(j\) 是关于 \(mid\) 的对称点。由回文串的对称性可以得出 \([id-p[id]+1,id]\) 和 \([id,id+p[id]-1]\) 两段一定完全相等,进一步推出以 \(j\) 为回文中心的串一定与以 \(i\) 为回文中心的串完全相等,所以 \(p[i]=p[j]\)。
因为 \(j\) 一定在 \(i\) 之前,符合递推的条件。\(j\) 的坐标可以 \(O(1)\) 求出,由坐标中点公式得出 \(j=id\times 2-i\),整个这种情况下的转移就可以 \(O(1)\) 实现了。
\(2\):不是很理想的情况
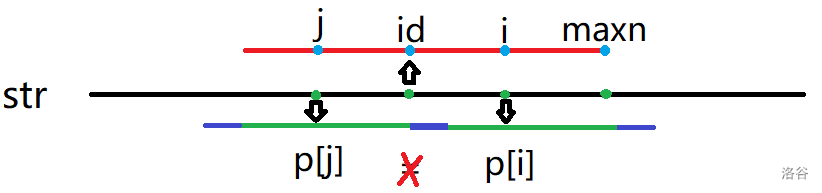
\(p[j]\) 出界的部分不能保证与 \(p[i]\) 出界的部分完全相同,此时 \(p[i]\) 不一定等于 \(p[j]\)。但是我们可以知道在 \([id-p[id]+1,id+p[id]-1]\) 这个范围内的部分完全相等,也就是说,在不超过这个范围的部分,以 \(j\) 为回文中心的串一定与以 \(i\) 为回文中心的串完全相等,观察以下图,其实就是 \(maxn-i+1\)。剩下的,就朴素吧。
由于每次朴素之后会把 \(maxn\) 往后推,所以时间复杂度还是 \(O(n)\)。
\(3\):很不理想的情况

无能为力了,只能朴素了。由于每次朴素之后会把 \(maxn\) 往后推,所以时间复杂度还是 \(O(n)\)。
具体实现的时候,可以首先判定是否为情况 \(3\),然后可以直接用一个 \(min\) 函数处理出情况 \(1\) 和情况 \(2\)。因为当处于情况 \(2\) 时,情况 \(2\) 的数值小于情况 \(1\);而处于情况 \(1\) 时,情况 \(1\) 的数值小于情况 \(2\)。最后在结合插入字符,朴素比较即可,注意更新 \(maxn\) 和 \(id\)。
这里实现时,\(maxn\) 的值是 \(i+p[i]\),是可以取到的最后一个位置的后一个位置,是不能取到的。所以代码中才写 \(maxn>i\),\(maxn-i\),这样写是为了节约一点点码量,但实际中不建议这么写,容易被误解。
p[1]=1;maxn=0;id=0;
for(int i=1;i<=l;i++){if(maxn>i)p[i]=min(p[id*2-i],maxn-i);else p[i]=1;while(str[i-p[i]]==str[i+p[i]])p[i]++;if(i+p[i]>maxn)maxn=i+p[i],id=i;}
由于插入字符的影响,我们注意到 \(p[i]-1\) 就是以 \(i\) 为中心的最长回文子串的长度,直接遍历一遍求最大值,就在 \(O(n)\) 的时间内解决了问题。
例题
例题 \(1\) :
P3805 【模板】manacher 算法
Manacher 模板题,不多赘述。
#include <bits/stdc++.h>
using namespace std;
int p[22000010],maxn=0,id=0,ans=0;
char stri[11000010],str[22000010];
int main()
{scanf("%s",stri);int l=strlen(stri);str[0]='!';for(int i=0;i<l;i++){str[i*2+1]='#';str[i*2+2]=stri[i];}str[l*2+1]='#';l=l*2+1;p[1]=1;maxn=0;id=0;for(int i=1;i<=l;i++){if(maxn>i)p[i]=min(p[id*2-i],maxn-i);else p[i]=1;while(str[i-p[i]]==str[i+p[i]])p[i]++;if(i+p[i]>maxn)maxn=i+p[i],id=i;}for(int i=1;i<=l;i++)ans=max(p[i]-1,ans);printf("%d",ans);return 0;
}
例题 \(2\) :
P1659 [国家集训队]拉拉队排练
看到题目中提到了回文串,自然联想到 Manacher 算法。
首先,如果一个回文串的长度为 \(n\)(\(n\) 为奇数且 \(n\ge1\)),则这个串同样也可以算作一个长度为 \(n-2\) 的回文串。因为这个回文串可以删去其最左右两边的两个字符,变成长度为 \(n-2\) 的串。由于原串是回文串,所以删去的字符相同,新串依旧是回文串。
有了这点,我们很容易得到一个思路:首先求出每个位置的最长回文子串,用一个桶记录下来。然后降序枚举(保证从高到低)最长回文子串长度,并进行数量累加,结果累乘,然后用快速幂求出值即可。
#include <bits/stdc++.h>
using namespace std;
long long p[2000020],t[2000020],maxn=0,id=0,ans=1,l=0,k=0,tj=0,tu=0,now=0,mod=19930726;
char stri[1000010],str[2000020];
long long power(long long a,long long p,long long m)
{long long x=a,ans=1;while(p){if(p%2==1)ans=ans*x%m;p/=2;x=x*x%m;}return ans;
}int main()
{scanf("%lld%lld",&l,&k);scanf("%s",stri);str[0]='!';for(int i=0;i<l;i++){str[i*2+1]='#';str[i*2+2]=stri[i];}str[l*2+1]='#';l=l*2+1;p[1]=1;maxn=0;id=0;for(int i=1;i<=l;i++){if(maxn>=i)p[i]=min(p[id*2-i],maxn-i);else p[i]=1;while(str[i-p[i]]==str[i+p[i]])p[i]++;if(i+p[i]>maxn)maxn=i+p[i],id=i;}for(int i=1;i<=l;i++)p[i]--;for(int i=1;i<=l;i++)t[p[i]]++;for(int i=1000020;i>0;i--){if(i%2==1){tj+=t[i];if(tj==0)continue;if(now+tj<=k)ans=ans*power(i,tj,mod)%mod,now+=tj;else {ans=ans*power(i,k-now,mod)%mod;printf("%lld",ans);return 0;}}}return 0;
}
例题 \(3\) :
P5446 [THUPC2018]绿绿和串串
由翻转操作的定义,得知翻转后的字符串一定是长度为奇数的回文串,再次联想到 Manacher。由于回文串长度为奇数,所以不用在空隙处插入字符。
性质 \(1\):如果一个位置 \(i\),其最长回文串延伸到字符串末尾,那么这个位置一定可以取到。
证明:
设字符串为 \(S\),如果这个位置可以取到,最终翻转形成的串一定为 \(Q+S_i+Q\)(\(Q\) 为 \(i\) 前所有字符组成的字符串)。因为其最长回文串延伸到字符串末尾,设不算位置 \(i\) 的单边的回文部分为 \(H\),则原字符串可以写作:(\(Q_0=Q-H\))
最终翻转形成的串可以写作:
因为给出的字符串可以是最终翻转形成的字符串的前缀,对比二式发现给出的字符串一定为最终翻转形成的字符串的前缀,所以这个位置可以取到,结论得证。
性质 \(2\):在不属于性质 \(1\) 的前提下,如果一个位置 \(i\),其最长回文串向左延伸到字符串第一个字符,向右延伸到可以取到的位置,那么这个位置一定可以取到。
证明:
由于不属于性质 \(1\),所以必须回文串从头开始,否则无法保证回文部分之前的字符与之后的字符完全相等,所以要求最长回文串向左延伸到字符串第一个字符。
如果最长回文串向右延伸到可以取到的位置,那么相当于再翻转后的字符串是符合要求的,所以这个能翻转出符合要求的字符串的位置也是符合要求的。又因为最长回文串向左延伸到字符串第一个字符,所以不会对再翻出的符合要求的字符串造成影响,结论得证。
因此,我们可以结合上面两条性质,从右往左进行递推。对于每一个点,首先判断其是否符合性质 \(1\),然后判断其是否符合性质 \(2\)。同时为了方便计算性质 \(2\),可以用一个数组记录每个位置是否可行。最后遍历一遍,输出可行的位置即可。
upd on 2024/8/9:更新了代码,原本的代码会被 hack。
#include <bits/stdc++.h>
using namespace std;
long long t,p[6000000],maxn=0,id=0,ans=0,book[6000000];
char s[6000000];
int main()
{scanf("%d",&t);while(t--){scanf("%s",s+1);s[0]='$';long long l=strlen(s);for(int i=1;i<=l;i++)p[i]=book[i]=0;s[l+1]='#',l--,p[1]=1,maxn=0,id=0;for(int i=1;i<=l;i++){if(maxn>i)p[i]=min(p[id*2-i],maxn-i);else p[i]=1;while(s[i-p[i]]==s[i+p[i]])p[i]++;if(i+p[i]>maxn)maxn=i+p[i],id=i;}for(int i=l;i>0;i--)if(i+p[i]==l+1)book[i]=1;else if(i==p[i])book[i]=book[i+p[i]-1];for(int i=1;i<=l;i++)if(book[i])printf("%d ",i);printf("\n");}return 0;
}后记
算法只是工具,现在很少直接考单纯的算法。Manacher 的题目重要的不是 Manacher 算法本身,而是其后的思维难度。——教练