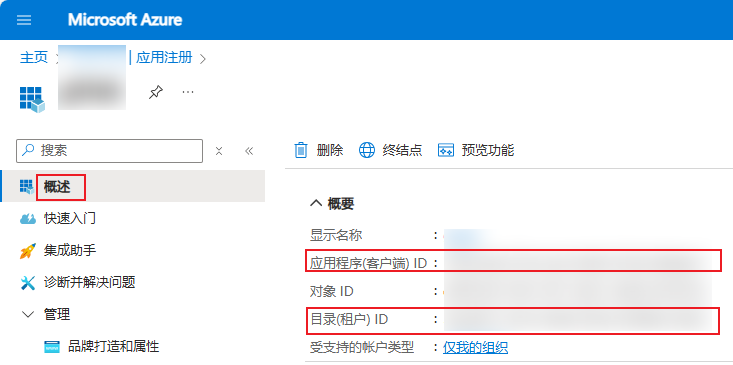
用多项式回归分析简单投掷数据-训练投石机数据预测模型

用多项式回归分析简单投掷数据

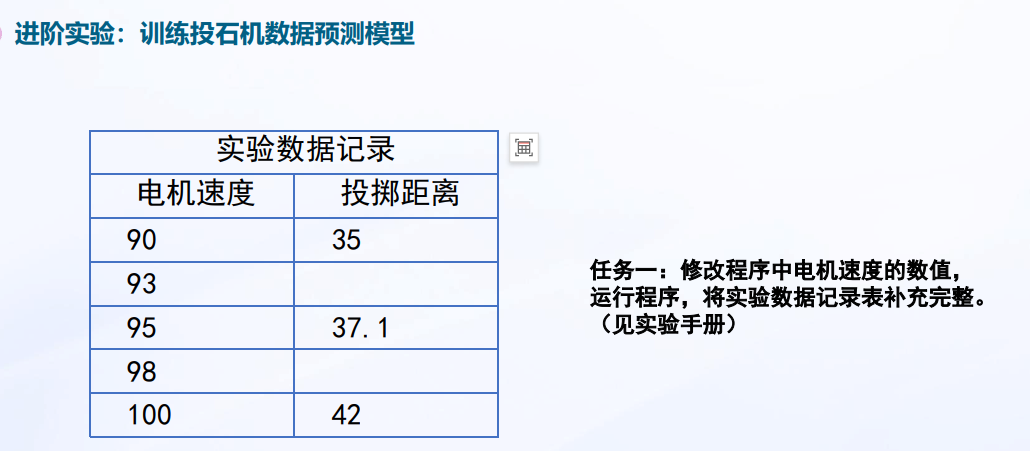
 进阶实验:训练投石机数据预测模型

问题描述:

 

(1)投掷角度不变，已知电机速度，如何得出实际投掷距离?

 

(2)其电机速度(motor_speed)和投掷距离(distance)的对应关系有什么关系?

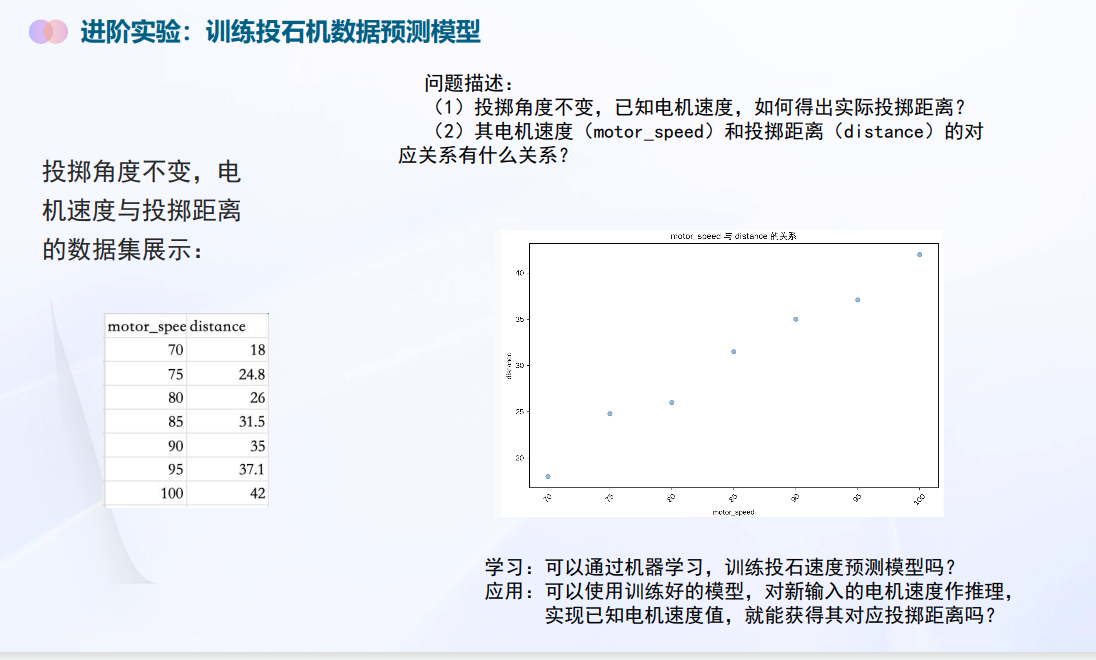
 投掷角度不变，电 机速度与投掷距离 的数据集展示：

 

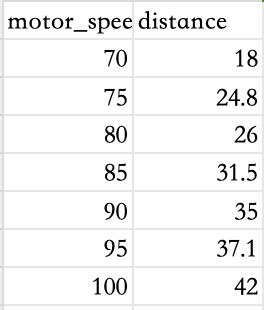
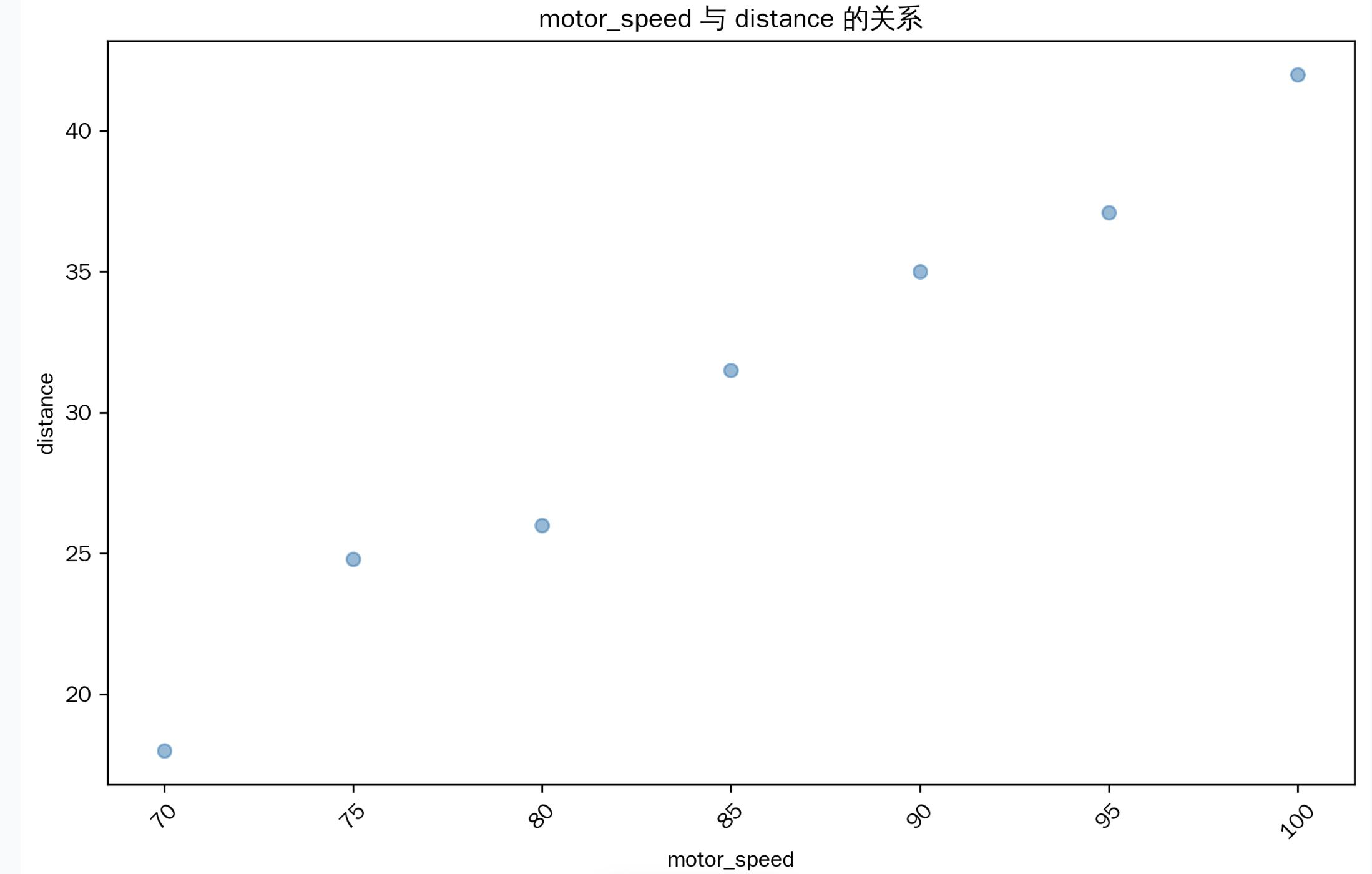
学习:i可以通过机器学习，训练投石速度预测模型吗?应用:可以使用训练好的模型，

对新输入的电机速度作推理实现已知电机速度值，就能获得其对应投掷距离吗?

 

 

 

 

 

 

 

 多项式回归

多项式回归（Polynomial Regression）是一种回归分析方法，它在模型中使用多项式方程来拟合数据。与线性回归不同，多项式回归可以捕捉变量之间的非线性关系，因此在处理更复杂的数据模式时非常有用。

多项式回归的数学形式

多项式回归的一般形式可以表示为：

y=β0​+β1​x+β2​x2+β3​x3+⋯+βn​xn+ϵ

 

其中：

• y 是因变量（目标）。
• x 是自变量（特征）。
• β0​,β1​,β2​,…,βn​ 是模型参数。
• ϵ 是误差项，通常假设为独立同分布的正态分布。

如何理解多项式回归

1. 线性回归的扩展：多项式回归是线性回归的扩展。线性回归假设变量之间的关系是线性的，而多项式回归通过引入自变量的高次项来捕捉非线性关系。
2. 拟合非线性数据：在实际应用中，数据之间的关系往往不是线性的。多项式回归通过使用多项式方程，可以更好地拟合这些非线性数据。
3. 多项式的阶数：多项式的阶数（n）决定了模型的复杂度。阶数越高，模型可以捕捉的非线性关系越复杂，但同时也可能带来过拟合（overfitting）的问题。
4. 参数估计：与线性回归类似，多项式回归的参数（β0​,β1​,β2​,…,βn​）可以通过最小化损失函数（如均方误差）来估计。

多项式回归的应用

多项式回归在许多领域都有应用，例如：

• 经济学：用于分析经济指标之间的非线性关系。
• 生物学：用于描述生物体的生长曲线。
• 工程学：用于拟合物理过程中的非线性数据。
• 机器学习：作为回归任务中的一种方法，用于预测连续的数值输出。

多项式回归的优缺点

优点：

• 可以捕捉变量之间的非线性关系。
• 模型形式灵活，可以通过调整多项式的阶数来适应不同的数据模式。

缺点：

• 阶数选择不当可能导致过拟合或欠拟合。
• 高阶多项式可能在数据的边缘区域出现较大的波动（龙格现象）。

总结

多项式回归是一种强大的回归分析工具，可以用于拟合非线性数据。通过引入自变量的高次项，它扩展了线性回归的适用范围。然而，使用多项式回归时需要谨慎选择多项式的阶数，以避免过拟合和龙格现象。

---

参考示例

• 多项式回归的数学形式：y=2+3x−0.5x2+0.1x3

• 

   

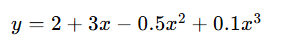
• 多项式回归的应用：假设你想分析广告支出与销售额之间的关系。通过使用多项式回归，你可以发现广告支出与销售额之间的非线性关系，从而更准确地预测销售额。

---

在选择使用线性回归还是多项式回归时，需要根据数据的特点和建模目标来判断。以下是两者的区别以及如何判断使用多项式回归的特点：

线性回归与多项式回归的区别

维度	线性回归	多项式回归
模型形式	输出是输入特征的线性组合	输出是输入特征的多项式组合
适用场景	数据呈现线性关系	数据呈现非线性关系
模型复杂度	参数少，模型简单	参数多，模型复杂
过拟合风险	容易欠拟合	容易过拟合
计算复杂度	计算速度快	随阶数增加，计算复杂度上升
解释性	易于理解和解释	解释性下降

如何判断使用多项式回归

1. 数据关系的可视化
   • 散点图：绘制自变量与因变量的散点图，观察数据点的分布。如果数据点呈明显的非线性趋势（如曲线形状），则多项式回归可能是更好的选择。
   • 残差分析：如果使用线性回归模型拟合数据后，残差图显示明显的模式（如中间有大量正残差的斑块），说明线性模型不适用，可以考虑多项式回归。
2. 数据的非线性特征
   • 当数据中存在明显的非线性关系时，线性回归可能无法很好地拟合数据，而多项式回归可以通过引入高次项来捕捉这些非线性关系。
3. 模型复杂度与泛化能力
   • 阶数选择：多项式回归的阶数越高，模型的拟合能力越强，但也更容易过拟合。通常建议从低阶多项式开始尝试，并通过交叉验证等方法选择最优的阶数。
   • 正则化：在使用多项式回归时，可以结合正则化方法（如岭回归或Lasso回归）来防止过拟合。
4. 应用场景
   • 复杂数据建模：多项式回归适用于需要捕捉复杂非线性关系的场景，如物理学中的曲线拟合、工程学中的性能曲线建模、医学研究中的剂量-效应关系等。
   • 简单数据建模：如果数据关系较为简单且呈现线性趋势，则线性回归更为合适，因为它简单、高效且易于解释。

总结

• 使用线性回归：当数据关系近似线性，且对模型的解释性和计算效率有较高要求时，线性回归是合适的选择。
• 使用多项式回归：当数据存在明显的非线性关系，且需要更灵活的模型来捕捉这些关系时，多项式回归更为适用

---

 

进阶实验：用多项式回归分析简单投掷数据

活动材料

• 多项式回归模型训练.ipynb
• data/投掷数据_速度与距离.csv
• data/投掷数据_完整.csv

活动目的

使用多项式回归算法，探究电机速度对投掷距离的影响。

背景知识

多项式回归算法是一种回归技术，相比于简单的线性回归，它可以拟合更复杂的数据模式，如投掷角度与投掷距离并非线性关系，在图表中表现为曲线而非直线。

数据说明

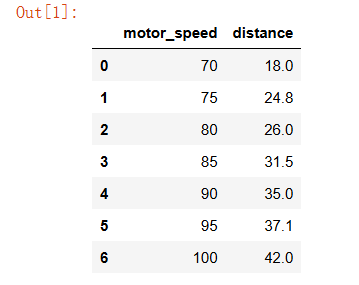
特征：motor_speed（在软件中配置的电机速度参数，无单位）

标签：distance（投掷距离，单位cm）

import pandas as pd
data = pd.read_csv('data/投掷数据_速度与距离.csv')
data

　　

 

体验步骤

1.导入库

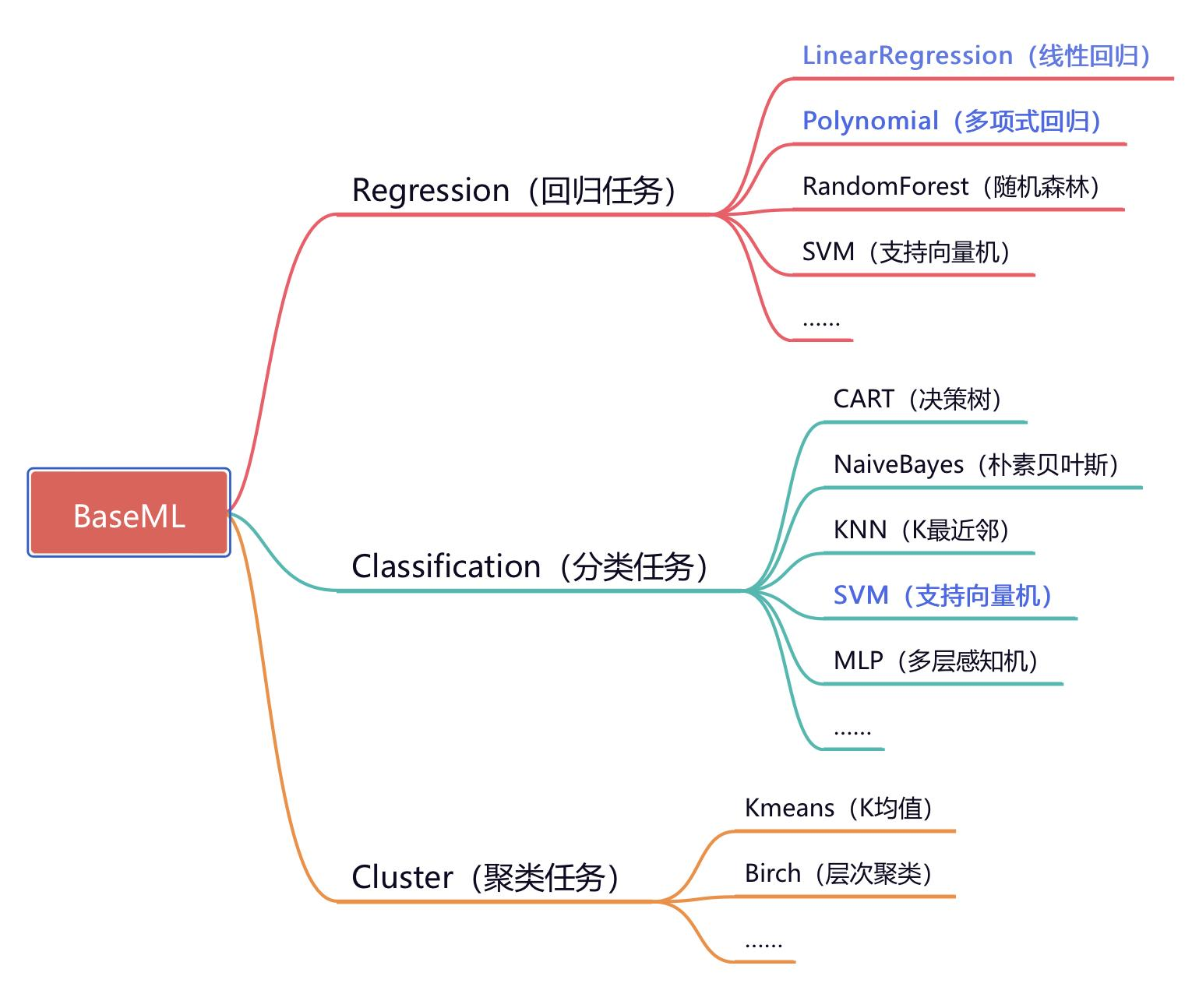
我们可以选择使用BaseML完成。

# 更新库，一个环境只需要运行一次
!pip install -U BaseML -i https://pypi.tuna.tsinghua.edu.cn/simple

　　

Looking in indexes: https://pypi.tuna.tsinghua.edu.cn/simple
Requirement already satisfied: BaseML in d:\xedu\env\lib\site-packages (0.1.5)
Requirement already satisfied: scikit-learn in d:\xedu\env\lib\site-packages (from BaseML) (1.3.0)
Requirement already satisfied: pandas in d:\xedu\env\lib\site-packages (from BaseML) (2.0.3)
Requirement already satisfied: numpy in d:\xedu\env\lib\site-packages (from BaseML) (1.24.4)
Requirement already satisfied: seaborn in d:\xedu\env\lib\site-packages (from BaseML) (0.12.2)
Requirement already satisfied: scikit-image in d:\xedu\env\lib\site-packages (from BaseML) (0.21.0)
Requirement already satisfied: matplotlib in d:\xedu\env\lib\site-packages (from BaseML) (3.3.1)
Requirement already satisfied: opencv-python>=4.1.2.30 in d:\xedu\env\lib\site-packages (from BaseML) (4.1.2.30)
Requirement already satisfied: yellowbrick in d:\xedu\env\lib\site-packages (from BaseML) (1.5)
Requirement already satisfied: certifi>=2020.06.20 in d:\xedu\env\lib\site-packages (from matplotlib->BaseML) (2023.7.22)
Requirement already satisfied: cycler>=0.10 in d:\xedu\env\lib\site-packages (from matplotlib->BaseML) (0.11.0)
Requirement already satisfied: kiwisolver>=1.0.1 in d:\xedu\env\lib\site-packages (from matplotlib->BaseML) (1.4.5)
Requirement already satisfied: pillow>=6.2.0 in d:\xedu\env\lib\site-packages (from matplotlib->BaseML) (10.0.0)
Requirement already satisfied: pyparsing!=2.0.4,!=2.1.2,!=2.1.6,>=2.0.3 in d:\xedu\env\lib\site-packages (from matplotlib->BaseML) (3.1.1)
Requirement already satisfied: python-dateutil>=2.1 in d:\xedu\env\lib\site-packages (from matplotlib->BaseML) (2.8.2)
Requirement already satisfied: pytz>=2020.1 in d:\xedu\env\lib\site-packages (from pandas->BaseML) (2023.3)
Requirement already satisfied: tzdata>=2022.1 in d:\xedu\env\lib\site-packages (from pandas->BaseML) (2023.3)
Requirement already satisfied: scipy>=1.8 in d:\xedu\env\lib\site-packages (from scikit-image->BaseML) (1.10.1)
Requirement already satisfied: networkx>=2.8 in d:\xedu\env\lib\site-packages (from scikit-image->BaseML) (3.1)
Requirement already satisfied: imageio>=2.27 in d:\xedu\env\lib\site-packages (from scikit-image->BaseML) (2.31.2)
Requirement already satisfied: tifffile>=2022.8.12 in d:\xedu\env\lib\site-packages (from scikit-image->BaseML) (2023.7.10)
Requirement already satisfied: PyWavelets>=1.1.1 in d:\xedu\env\lib\site-packages (from scikit-image->BaseML) (1.4.1)
Requirement already satisfied: packaging>=21 in d:\xedu\env\lib\site-packages (from scikit-image->BaseML) (23.1)
Requirement already satisfied: lazy_loader>=0.2 in d:\xedu\env\lib\site-packages (from scikit-image->BaseML) (0.3)
Requirement already satisfied: joblib>=1.1.1 in d:\xedu\env\lib\site-packages (from scikit-learn->BaseML) (1.3.2)
Requirement already satisfied: threadpoolctl>=2.0.0 in d:\xedu\env\lib\site-packages (from scikit-learn->BaseML) (3.2.0)
Requirement already satisfied: six>=1.5 in d:\xedu\env\lib\site-packages (from python-dateutil>=2.1->matplotlib->BaseML) (1.16.0)

 

# 导入库
from BaseML import Regression as reg
# 构建多项式回归模型
model = reg('Polynomial')
# 使用函数载入数据，并自动划分训练集和验证集
model.load_dataset('data/投掷数据_速度与距离.csv',type ='csv',split=True, x_column = [0],y_column=[1])# 训练模型
model.train()# 读取验证集进行验证并计算R平方值 此处数据量较小，数据集划分情况会在较大程度情况下影响R2值，不影响推理结果
model.valid(metrics='r2') # 载入验证数据
# 模型保存
model.save('models/model1.pkl')

　　

 

Saving model checkpoints...
Saved successfully!

7.模型应用

from BaseML import Regression as reg # 从库文件中导入回归任务模块
model = reg('Polynomial') # 构建多项式回归模型
model.load('models/model1.pkl')data = [[97]] # 指定一个不存在于数据中的电机速度result= model.inference(data)# 进行模型推理
print(f"模型返回的预测结果是：投掷距离={result[0][0]:.2f}cm")

　　

模型返回的预测结果是：投掷距离=39.30cm

 

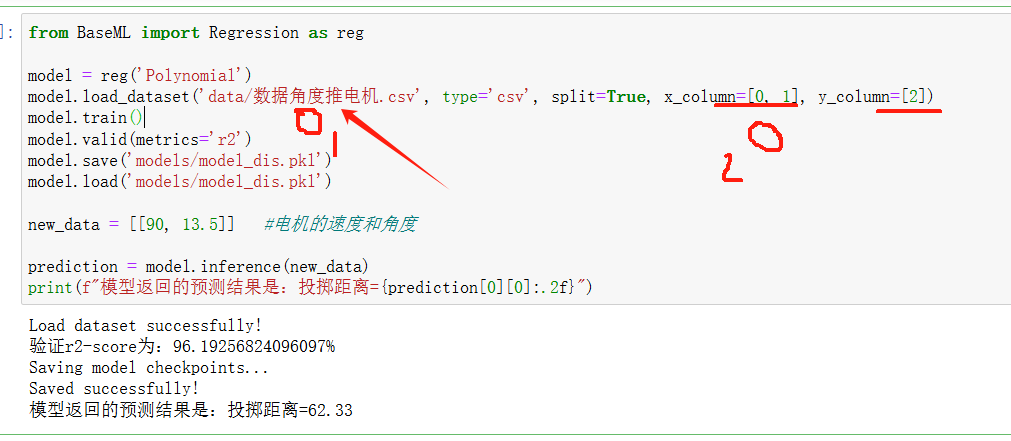
用角度和电机速度预测投掷物距离

请在csv中找到带有角度和电机速度的csv文件，并将文件名填写到填空处

from BaseML import Regression as regmodel = reg('Polynomial')
model.load_dataset('data/数据角度推电机.csv', type='csv', split=True, x_column=[0, 1], y_column=[2])
model.train()
model.valid(metrics='r2')
model.save('models/model_dis.pkl')
model.load('models/model_dis.pkl')new_data = [[90, 13.5]]   #电机的速度和角度prediction = model.inference(new_data)
print(f"模型返回的预测结果是：投掷距离={prediction[0][0]:.2f}")

　　1）可以修改，数据csv文件的列数据位置， 从0开始。

2）可以修改 x_xolumn【参数】给定的数据下标位置，  推理得到  y_column【2】 的结果。 可以修改这里的下标值，下标对应的数据库csv数据的列的序号。 从做到右，从0开始计数

 

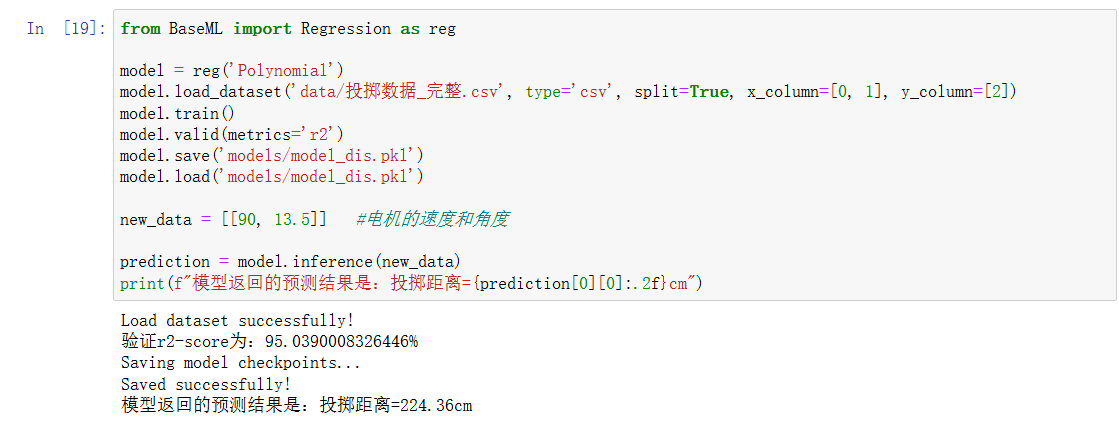
在已知目标投掷距离和发射角度的情况下，如何预测合适的电机速度？

思路提示1：修改数据集csv文件中的特征与标签，保存为新文件投掷数据2.csv并读取。

思路提示2：通过代码实现特征与标签的读取, 如下方代码实现的功能就是：读取xx.csv文件中的第0、1、2、3列作为特征，第4列作为标签。

model.load_dataset('data/投掷数据.csv', type ='csv',split=True,x_column=[0,1,2,3],y_column=[4])

from BaseML import Regression as regmodel = reg('Polynomial')
model.load_dataset('data/投掷数据_完整.csv', type='csv', split=True, x_column=[0, 1], y_column=[2])
model.train()
model.valid(metrics='r2')
model.save('models/model_dis.pkl')
model.load('models/model_dis.pkl')new_data = [[90, 13.5]]   #电机的速度和角度prediction = model.inference(new_data)
print(f"模型返回的预测结果是：投掷距离={prediction[0][0]:.2f}cm")

　　

 训练投石机数据预测模型