本文相关的TryHackMe实验房间链接:https://tryhackme.com/r/room/cryptographybasics
本文相关内容:了解关于密码学和对称加密的基础知识。

介绍

你是否想知道如何防止第三方阅读你的消息?你的应用程序或网络浏览器如何与远程服务器建立安全通道?所谓安全,是指任何人都无法读取或更改交换的数据;此外,我们可以确信我们正在与真实服务器连接。由于密码学,这些要求都得到了满足。
密码学为我们的数字世界奠定了基础。虽然网络协议使遍布全球的设备能够进行通信,但加密技术使信任这种通信成为可能。
本文是关于密码学的简单介绍。除了要求你具备使用 Linux 命令行的基本能力外,并没有其他任何先决学习条件。
Learning Objectives 学习目标
完成此房间后,你将学到以下内容:
- Cryptography key terms:密码学关键术语;
- Importance of cryptography:密码学的重要性;
- Caesar Cipher:凯撒密码(一种古老的加密算法);
- Standard symmetric ciphers:标准对称加密算法;
- Common asymmetric ciphers:常见的非对称加密算法;
- Basic mathematics commonly used in cryptography:密码学中常用的数学基础。
密码学的重要性
密码学的最终目的是确保在攻击者存在的情况下进行安全通信。术语“安全”包括所传送数据的机密性和完整性。密码学可以定义为安全通信和数据保护技术的实践和研究,我们预计攻击者和第三方的存在。换句话说,这些对手不应该能够披露或更改消息的内容。
密码学用于保护机密性、完整性和真实性。在这个时代,你每天都使用密码学,并且几乎可以肯定你是通过加密连接阅读本文的。考虑以下使用加密技术的场景:
- 当你登录 TryHackMe 时,你的凭据将被加密并发送到服务器,以便任何人都无法通过窥探你的连接来检索它们。
- 当你通过SSH连接时,你的SSH客户端和服务器会建立一条加密隧道,因此没有人可以窃听你的会话。
- 当你进行网上银行时,你的浏览器会检查远程服务器的证书,以确认你正在与银行的服务器而不是攻击者的服务器进行通信。
- 下载文件时,如何检查文件是否正确下载?密码学提供了一种通过哈希函数来确认你的文件与原始文件相同的解决方案。
正如你所看到的,你很少需要直接与密码学交互,但它的解决方案和影响在数字世界中无处不在。考虑这样的情况:一家公司想要处理信用卡信息并处理相关交易。在处理信用卡时,公司必须遵循并执行支付卡行业数据安全标准(PCI DSS-Payment Card Industry Data Security Standard)。在这种情况下,PCI DSS可确保存储、处理和传输与卡信用相关的数据的最低安全级别。如果你检查用于大型组织的PCI DSS ,你将了解到数据在存储(静态)和传输(动态)时都应该加密。
就像处理支付卡详细信息需要遵守PCI DSS一样,处理医疗记录也需要遵守各自的标准。与信用卡不同,处理医疗记录的标准因国家而异。处理医疗记录时应考虑的法律和法规示例包括:美国的HIPAA(健康保险流通和责任法案-Health Insurance Portability and Accountability Act)和HITECH(经济和临床健康健康信息技术-Health Information Technology for Economic and Clinical Health)、欧盟的GDPR(通用数据保护条例-General Data Protection Regulation)、英国的DPA(数据保护法-Data Protection Act)。尽管该列表并不详尽,但它提供了医疗保健提供者应根据其所在国家/地区考虑的法律要求的想法。这些法律和法规表明,加密技术是一种必需品,应该存在,但通常对用户的直接访问是隐藏的。
答题
处理信用卡(credit card)信息需要什么标准?
支付卡行业数据安全标准-Payment Card Industry Data Security Standard (PCI DSS).

从明文到密文
在介绍关键术语之前,让我们先从一个例子开始。我们从要加密的明文开始。明文是可读的数据;它可以是任何东西,从简单的“你好”、猫的照片、信用卡信息或医疗健康记录。从密码学的角度来看,这些都是等待加密的“明文”消息。明文与适当的密钥一起通过加密(encryption)函数;加密函数返回密文。加密函数是密码算法的一部分;密码算法是一种将明文转换为密文的算法,反之亦然。

为了恢复明文,我们必须通过解密(decryption)函数传递密文和正确的密钥,这将给我们原始的明文。如下图所示。

我们刚刚介绍了几个新术语,我们需要学习它们才能理解任何有关密码学的文本,关于这些术语的解释如下所示:
- 明文(Plaintext)是加密之前的原始可读消息或数据;它可以是文档、图像、多媒体文件或任何其他二进制数据。
- 密文(Ciphertext)是加密后消息的杂乱、不可读版本;在理想情况下,除了原始明文的大概大小之外,我们无法获得任何有关原始明文的信息。
- 密码算法(Cipher)是一种将明文转换为密文并再次转换回来的算法或方法;密码算法通常由数学家开发。
- 密钥(Key)是密码算法用于加密或解密数据的一串位;一般来说,加密所使用的密码算法是公共知识,然而,密钥必须是保密的,除非它是非对称加密中的公钥。我们将在后面的小节中介绍非对称加密。
- 加密(Encryption)是使用密码算法和密钥将明文转换为密文的过程;与密钥不同,密码算法的选择可以是公开的。
- 解密(Decryption)是加密的逆过程,使用密码算法和密钥将密文转换回明文;尽管密码算法是公开的,但是在不知道密钥的情况下恢复明文应该是不可能的(不可行)。
答题
你怎么称呼加密的明文?
Ciphertext
返回明文的过程叫什么?
Decryption

历史上的密码学
密码学的历史悠久,可以追溯到公元前 1900 年的古埃及。然而,历史上最简单的密码算法之一是公元前一世纪的凯撒密码。这个密码算法的想法很简单:将每个字母移动一定的数字来加密消息。
考虑以下示例:
- Plaintext(明文):
TRYHACKME - Key: 3 (假设是右移3)
- Cipher(密码算法): Caesar Cipher(凯撒密码)
我们很容易算出T变成W,R变成U,Y变成B,等等。正如你所注意到的,一旦到达 Z,我们就从头开始,如下图所示。因此,我们得到了WUBKDFNPH的密文。

为了解密,我们需要以下信息:
- Ciphertext(密文):
WUBKDFNPH - Key: 3
- Cipherr(密码算法): Caesar Cipher(凯撒密码)

对于加密,我们向右移动三位;为了解密,我们需要向左移动三位并恢复原始明文,如上图所示。如果有人给你一个密文并告诉你它是使用凯撒密码加密的,那么恢复原始文本将是一项微不足道的任务,因为只有25个可能的密钥。英文字母为26个字母,移位26将保持字母不变;因此,使用凯撒密码进行加密需要25个有效密钥。下图展示了如何通过尝试所有可能的密钥来成功解密;在这种情况下,我们通过Key = 5 恢复了原始消息。因此,按照今天的标准,当密码算法是公开的时,凯撒密码被认为是一种不安全的加密方式。

你会在电影和密码学书籍中发现更多的历史上的密码算法,示例包括:
- The Vigenère cipher from the 16th century:16 世纪的维吉尼亚密码;
- The Enigma machine from World War II:二战时期的恩尼格玛密码机;
- The one-time pad from the Cold War:冷战时期的一次性密码本。
答题
我们已经知道XRPCTCRGNEI是使用凯撒密码进行加密的,那么它的原始明文是多少呢?
访问:https://cryptii.com/pipes/caesar-cipher 或者 https://www.dcode.fr/caesar-cipher

ICANENCRYPT

加密类型
加密的两个主要类别是对称(symmetric)和非对称(asymmetric)。
对称加密
对称加密又被称为对称密码使用法(cryptography),它表示使用相同的密钥来加密和解密数据,如下图所示。我们必须对密钥进行保密;它也可被称为私钥密码使用法(cryptography)。此外,将密钥传达给预期的各方可能具有挑战性,因为它需要安全的通信通道。维护密钥的保密性可能是一项重大挑战,尤其是在有很多收件人的情况下。当遇到强大的攻击者时,问题会变得更加严重。例如,考虑工业间谍活动的威胁。

考虑一个简单的情况,你创建了一个受密码保护的文档以便与同事共享。你可以轻松地将加密文档通过电子邮件发送给你的同事,但很可能你无法通过电子邮件将密码发送给他们。原因是任何有权访问其邮箱的人都可以访问受密码保护的文档及其密码。因此,你需要想一个不同的方式,即通道(隧道),来共享密码。除非你想到一个安全、可访问的隧道,否则一种解决方案是亲自会面并向他们传达具体的密码。
对称加密的示例有DES(数据加密标准-Data Encryption Standard)、3DES(三重DES)和AES(高级加密标准-Advanced Encryption Standard)。
- DES于 1977 年被采用为标准,并使用 56 位密钥。随着计算能力的进步,1999 年,一个DES密钥在不到 24 小时内被成功破解,这推动了它向 3DES 的转变。
- 3DES是三次DES ;因此,尽管有效安全性为 112 位,但密钥大小为 168 位。当DES不再被认为是安全时,3DES 更像是一种临时解决方案。 3DES 已于 2019 年被弃用,由AES取代;但是,在某些遗留系统中仍然可以找到它。
- AES于 2001 年被采用为标准。其密钥大小可以是 128、192 或 256 位(bits)。
在各种应用中还有更多的对称加密密码算法;然而,它们尚未被采纳为标准。
非对称加密
与使用相同密钥进行加密和解密的对称加密不同,非对称加密使用的是一对密钥,一个用于加密,另一个则用于解密,如下图所示。为了保护机密性,非对称加密或非对称密码使用法(cryptography)将使用公钥对数据进行加密;因此,它也被称为公钥密码使用法(cryptography)。

例如 RSA算法、Diffie-Hellman算法和椭圆曲线加密(ECC)算法。该过程中涉及的两个密钥被称为公钥(public key)和私钥(private key)。使用公钥加密的数据可以使用私钥进行解密,你的私钥需要保密,因此得名。
非对称加密往往速度较慢,并且许多非对称加密密码算法会使用比对称加密更大的密钥。例如,RSA算法使用2048位、3072位和4096位密钥; 2048位是建议的最小密钥大小。 Diffie-Hellman算法还建议最小密钥大小为2048位,但它通常使用3072位和4096位密钥来增强安全性。另一方面,ECC算法可以使用较短的密钥实现同等的安全性,例如,使用256位密钥,ECC算法提供的安全级别可与3072位RSA密钥相媲美。
非对称加密基于一组特定的数学问题,这些问题很容易在一个方向上进行计算,但极难被逆转。在这里,极其困难进行逆向运算意味着实际上不可行。例如,我们可以将逆向非对称加密作为一个数学问题来看待,但使用当今的技术需要很长时间(例如数百万年)才能解决它。
我们将在其他文章中介绍各种非对称加密密码。目前,需要注意的重要一点是,非对称加密为你提供了与所有人共享的公钥和你需要保密的私钥。
术语摘要
Alice 和 Bob是密码学示例中常用的虚构人物,代表试图进行安全通信的两方。对称加密(Symmetric encryption)是一种加密和解密使用相同密钥的方法,因此,该密钥必须保持安全,并且不得泄露给除预期方之外的任何人。非对称加密(Asymmetric encryption)是一种使用两个不同密钥的方法,包括专门用于加密的公钥和专门用于解密的私钥。
答题
你应该相信 DES 吗? (是/否-Yea/Nay)
Nay
AES 何时被采用作为加密标准?
2001

密码学中的数学基础
现代密码学的基石在于数学。为了演示一些基本算法,我们将介绍在各种算法中经常被使用的两种数学运算:
- XOR Operation:异或运算
- Modulo Operation:模运算
XOR Operation 异或运算
XOR是“异或-exclusive OR”的缩写,是二进制算术中的一种逻辑运算,在各种计算和密码应用中发挥着至关重要的作用。在二进制中, XOR将会比较两个二进制位,如果位不同则返回 1(真),如果位相同则返回 0(假),如下真值表所示。该运算通常用符号⊕或^表示。
tips:同0异1。

如果这是你第一次使用真值表,那么它会显示所有可能的结果。上面的异或真值表说明了所有四种情况:0 ⊕ 0 = 0、0 ⊕ 1 = 1、1 ⊕ 0 = 1 和 1 ⊕ 1 = 0。
让我们考虑一个示例,我们要将XOR应用于二进制数 1010 和 1100。在这种情况下,我们逐位执行异或操作:1 ⊕ 1 = 0、0 ⊕ 1 = 1、1 ⊕ 0 = 1 和 0 ⊕ 0 = 0,结果是 0110。
你可能想知道XOR如何在密码学中发挥作用。 XOR有几个有趣的属性,使其在密码学和错误检测中很有用。一个关键属性是,对某个值与其自身进行异或运算会得到 0,而对任何与 0 的值进行异或运算会使其保持不变。这意味着对于任何二进制值 A,A ⊕ A = 0,并且 A ⊕ 0 = A。此外, XOR是可交换的,即 A ⊕ B = B ⊕ A。并且它还是可结合的,即 (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C)。
让我们看看如何在密码学中利用上述内容。我们将演示如何将XOR用作基本的对称加密算法。考虑二进制值 P 和 K,其中 P 是明文,K 是密钥。密文为C = P ⊕ K。
现在,如果我们知道 C 和 K,我们就可以恢复 P。我们从 C ⊕ K = (P ⊕ K) ⊕ K 开始。我们知道 (P ⊕ K) ⊕ K = P ⊕ (K ⊕ K) ,因为XOR是可结合的。此外,我们知道 K ⊕ K = 0;因此, C ⊕ K =(P ⊕ K) ⊕ K = P ⊕ (K ⊕ K) = P ⊕ 0 = P。换句话说, XOR可以作为一种简单的对称加密算法。实际上,情况比较复杂,因为此处我们需要的密钥和明文一样长。
Modulo Operation 模运算
我们在密码学中经常遇到的另一个数学运算是模运算,通常写为 % 或作为 mod 。模运算, X%Y ,就是X除以Y的余数。在日常生活计算中,我们更注重除法的结果,而不是余数的结果,但余数在密码学中发挥着重要作用。
在解决一些密码学练习时,你可能需要处理大量数字。如果你使用普通的计算器无法进行处理,我们建议使用 Python 等编程语言来完成计算过程。 Python有一个内置的int类型,可以处理任意大小的整数,并根据需要自动切换到更大的类型。许多其他编程语言都有专门的大整数库。如果你更喜欢在线的数学计算,请考虑使用WolframAlpha 。
让我们考虑以下几个例子:
- 25%5 = 0 ,因为 25 除以 5 是 5,余数为 0,即 25 = 5 × 5 + 0
- 23%6 = 5 ,因为 23 除以 6 等于 3,余数为 5,即 23 = 3 × 6 + 5
- 23%7 = 2 ,因为 23 除以 7 等于 3,余数为 2,即 23 = 3 × 7 + 2
关于模运算需要记住的重要一点是它是不可逆的。如果我们给出方程 x%5 = 4 ,则会有无限个x值将满足这个方程。
模运算始终返回小于除数的非负结果。这意味着对于任何整数 a 和正整数 n ,结果 a%n 永远在 0 到 n − 1 范围内。
答题
访问:https://www.wolframalpha.com/
异或运算1001⊕1010的结果是什么?(同0异1)
0011
模运算118613842%9091的结果是什么 ?
3565
模运算60%12的结果是什么 ?
0

本文小结
在本文内容中,我们了解了密码学的重要性以及它能够解决的一些问题。我们还简单介绍了对称和非对称加密算法。最后,我们还介绍了异或运算和模运算。在后继的学习中,我们还将学习各种非对称加密算法的运用,并了解它们将如何解决我们在数字世界中面临的问题。
在进入下一个阶段的学习之前,请确保你已记下本文内容中已经介绍的所有关键术语和概念。
 了解关于密码学和对称加密的基础知识。
了解关于密码学和对称加密的基础知识。
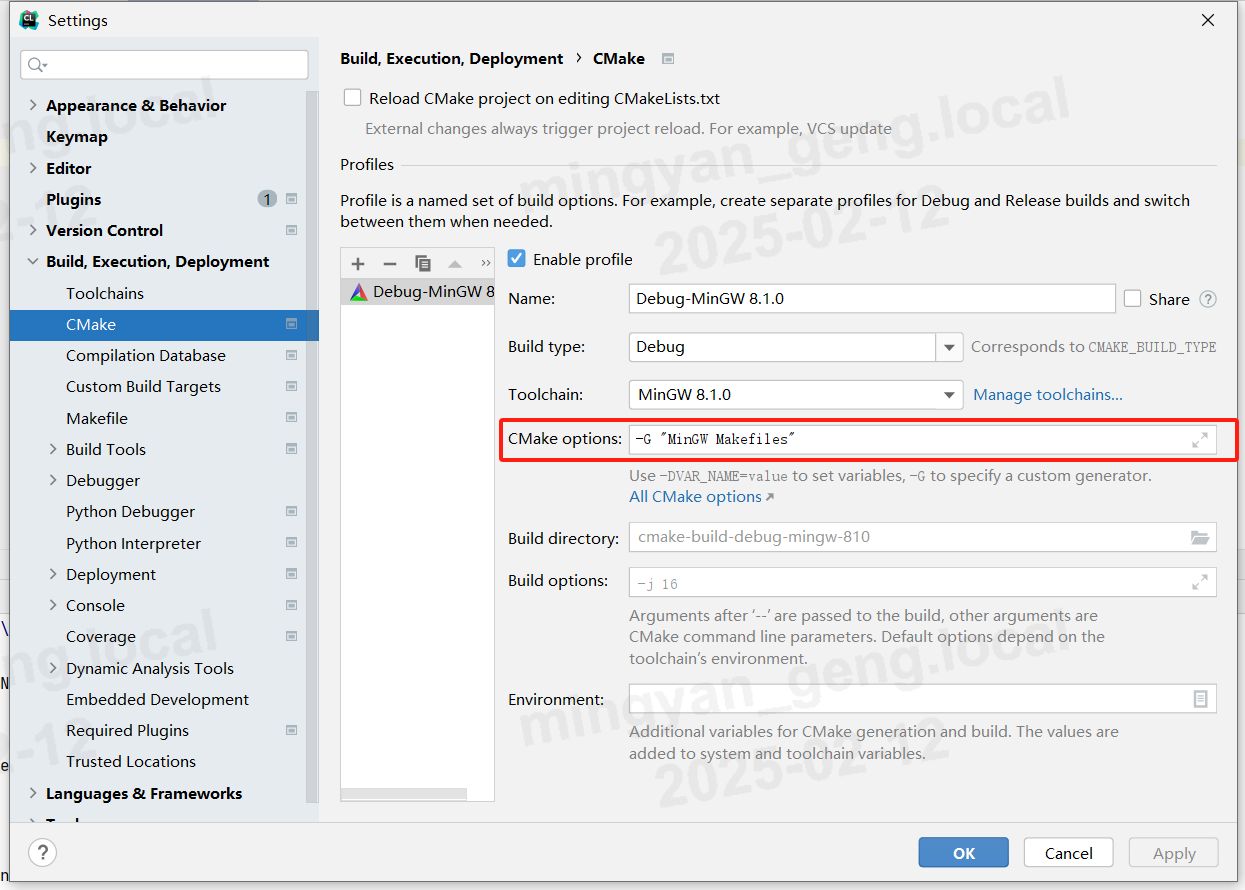
![[tldr]通过指令获取github仓库的单个文件的内容](https://img2024.cnblogs.com/blog/3573053/202502/3573053-20250212185738941-1108203471.png)