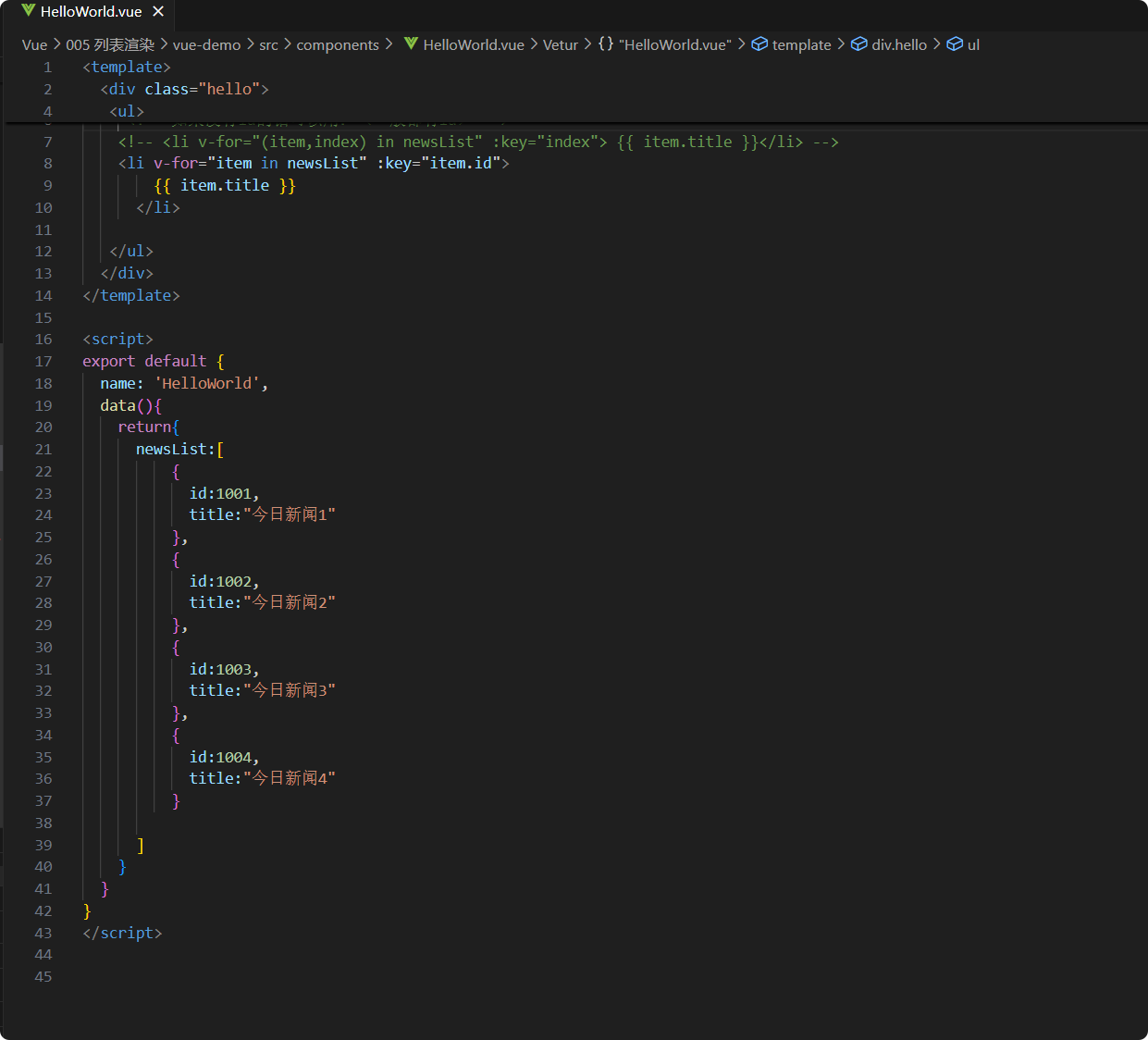
针孔相机(Pinhole camera)
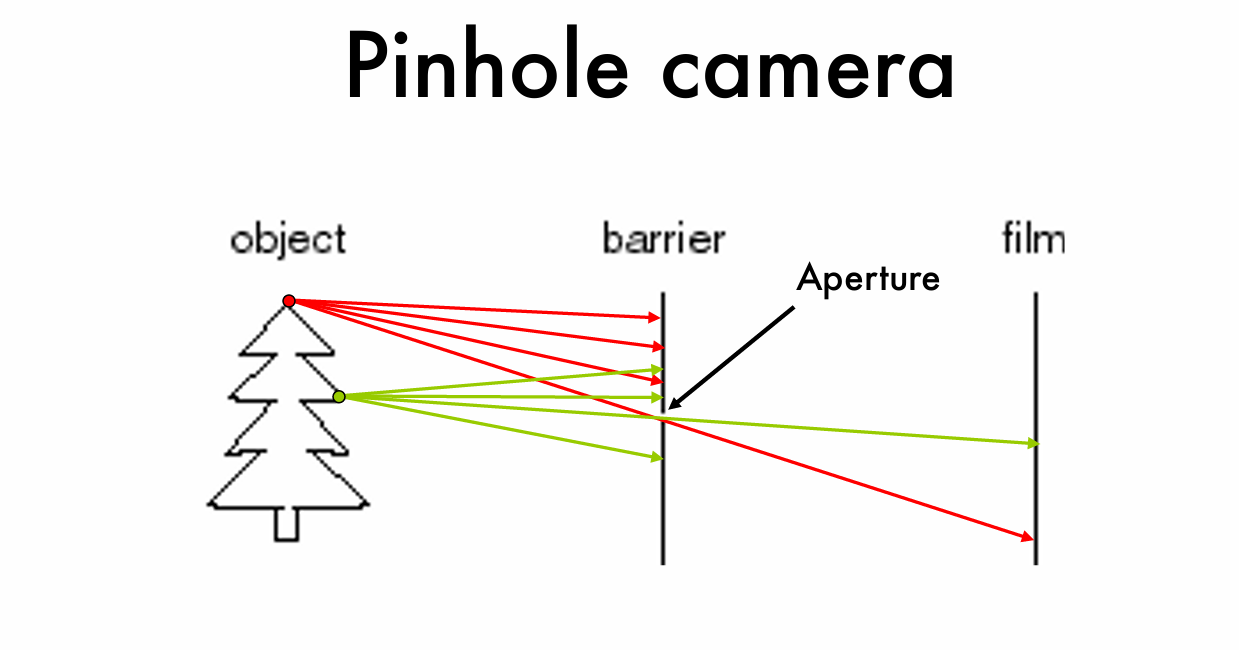
如图所示,这是一个比较简单的针孔相机模型,这里的树是我们需要拍摄的物体,记作object,从物体身上不同点发出不同颜色的光线。
barrier表示的是障碍,它位于物体和胶片之间,具有阻挡光线的作用。
Aperture 表示针孔,即障碍物上的一个小孔。光线通过这个小孔投射到胶片上。
film:表示胶片,光线最终在胶片上成像。
即针孔相机通过添加一个障碍物以阻挡大部分光线,只允许少量光线通过针孔,从而使成像更清晰,减少图像模糊。
进一步地,我们将针孔相机的模型进行简化,得到如下图所示模型:
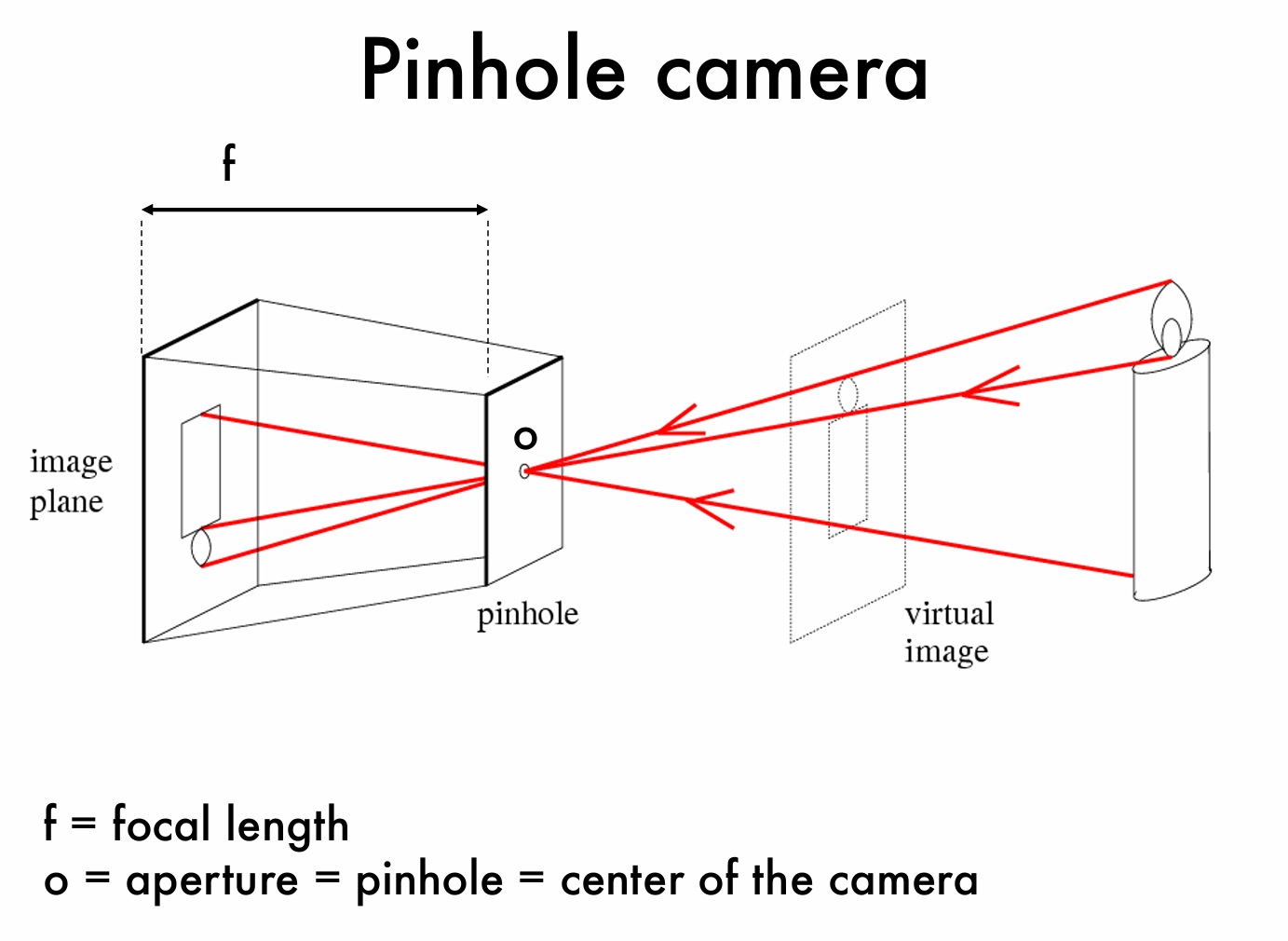
物体的光线打出来,首先形成虚像(virtual image),并通过针孔进入相机内部并在图像平面汇聚成像,从而在图像平面形成了倒立的像,我们记图像平面到针孔的距离为焦距 \(\mathbf{f}\)。
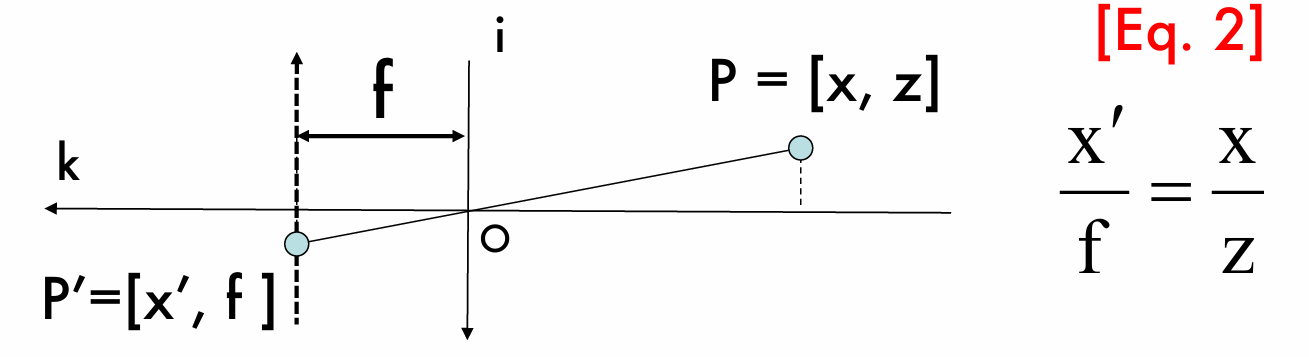
如果我们以针孔为原点建立坐标系,便能够将三维空间上的点映射到二维平面上,如图所示:

假设三维空间点的坐标为 (x, y, z) ,图像平面上成像点坐标为 (x', y') ,则我们能够通过相似三角形原理推导得出他们之间的关系,推导过程也很简单:
接下来我们需要讨论一个问题:在我们简化相机模型中,我们将针孔视为了一个点,但是在实际的相机模型中,针孔是有大小的,因此我们需要讨论一下针孔的大小对于图像的形成会有什么样的影响呢?
事实上,如果如果相机的针孔太大,将会导致形成的图像不够清晰;但针孔太小,进入相机的光线不足,可能导致成像过暗等问题,解决办法是添加镜头,通过添加镜头可以在缩小光圈保证清晰度的同时,汇聚更多光线,改善成像质量。
相机与镜头
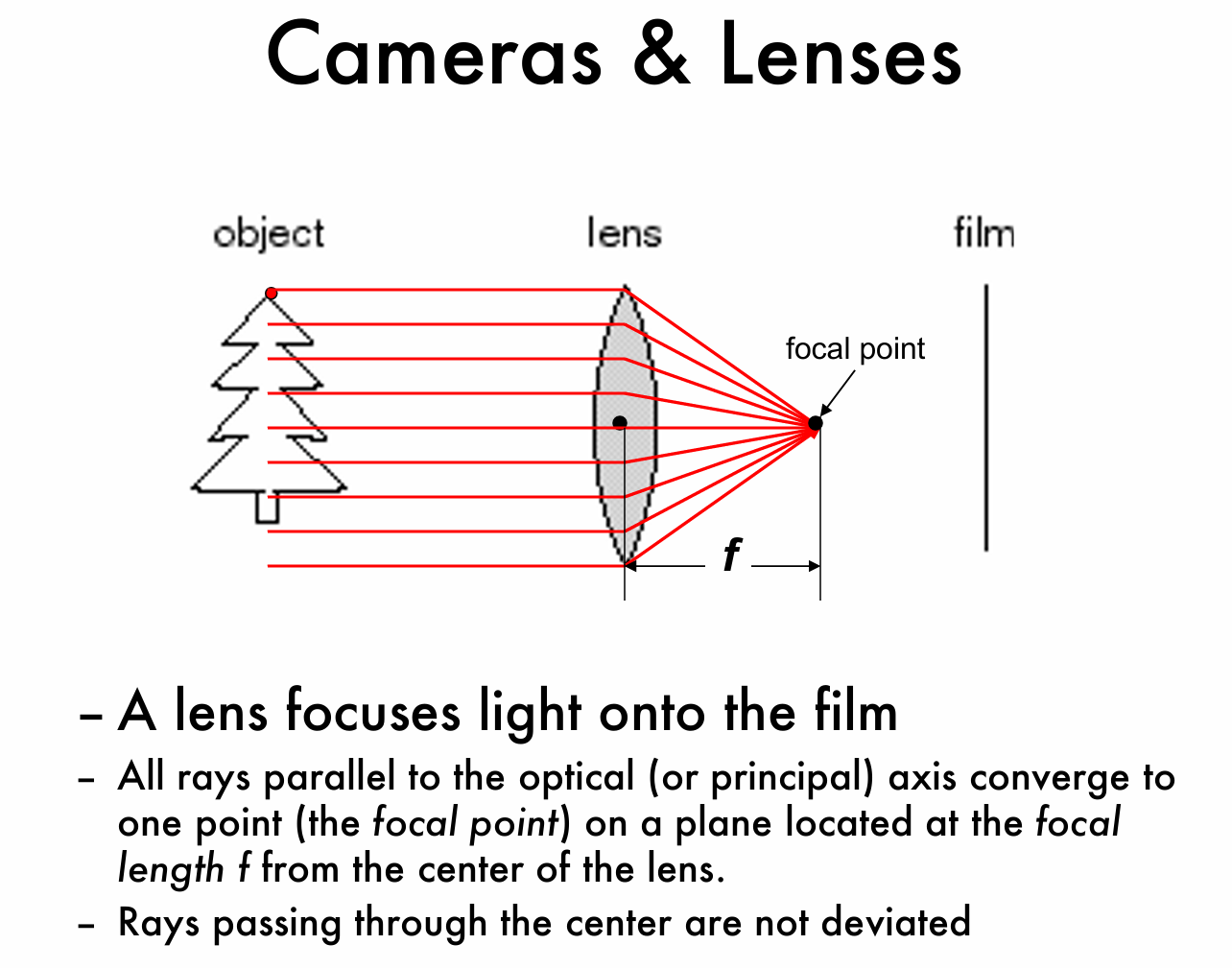
为了解决以上问题,人们想到了利用透镜作为镜头,它能够起到汇聚光线的作用,从物体上一个点发出了许多不同的光线,经过镜头又重新汇聚到图像平面的同一点,如图所示:
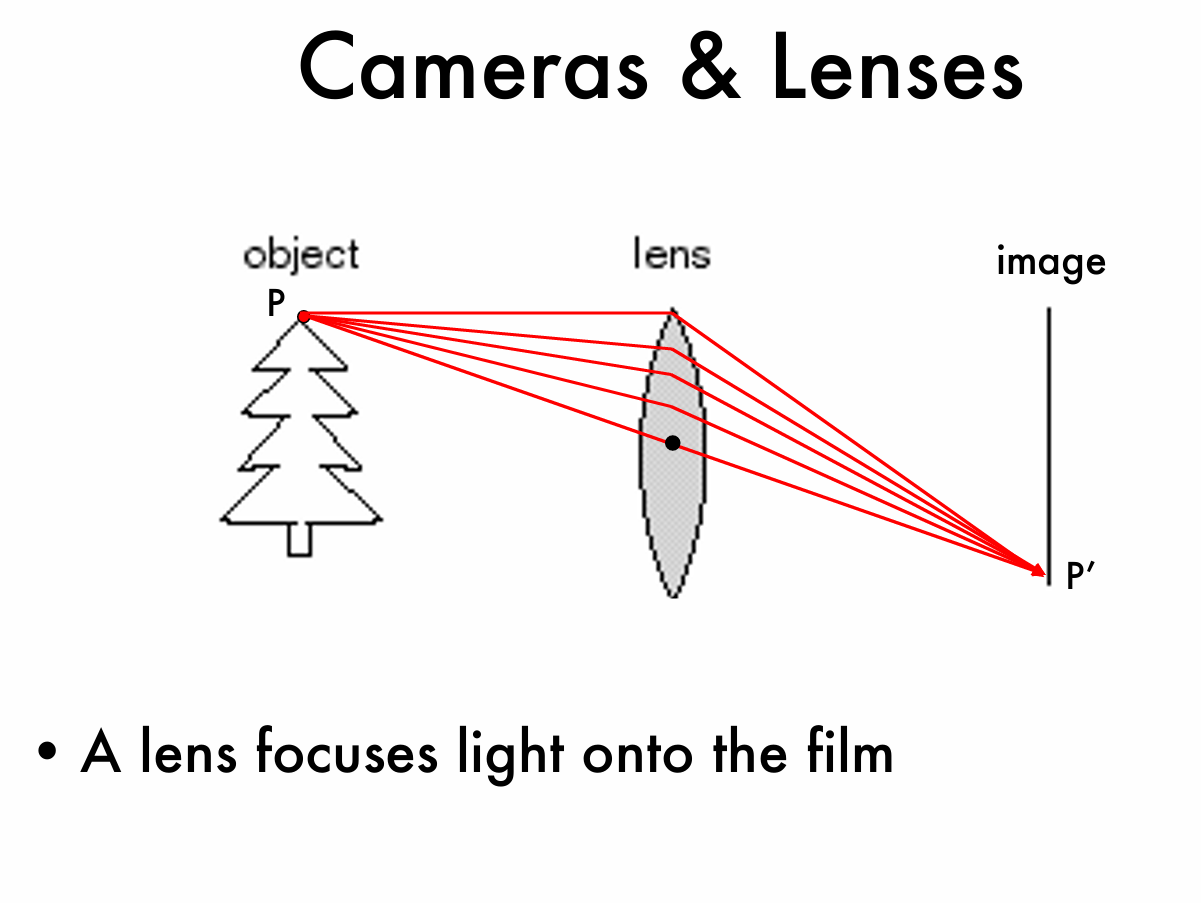
镜头在相机成像中的作用是使光线聚焦,但是只有当物体处于特定距离时,才能在成像平面上形成清晰的像,上述现象与景深概念紧密相连,景深描述了在镜头前方能够形成清晰图像的空间深度范围,如果距离太近或者太远光线无法汇聚到成像平面上,则会在平面前后发散,这种现象被称为失焦(Out of focus)。
如果从物体上一点发出多条光线都与光轴(或主轴)平行,经过镜头后汇聚到一个点,则这个点叫做焦点,焦点到镜头中心的距离叫做焦距 \(\mathbf{f}\)。并且还有一条穿过镜头中心的光线,其传播方向未发生改变。
近轴折射模型(Paraxial refraction model)

近轴折射模型也是一个将三维世界的点转化为二维图像平面的点的方法,由斯涅尔定理我们能够得到公式:
\(\begin{cases}x' = z'\frac{x}{z} \\ y' = z'\frac{y}{z} \end{cases}\),这里的 \(z'=\mathbf{f}+z_0\),但由于近轴折射模型,假设物体足够远,\(z'\) 近似等于焦距 \(\mathbf{f}\) ,此时我们就可以省略 \(z_0\) 用焦距 \(\mathbf{f}\) 来替代 \(z'\) ,从而得到了这个简化公式,即 \(\begin{cases}x' = f\frac{x}{z} \\ y' = f\frac{y}{z} \end{cases}\) 。同时课件中也给了我们计算焦距的公式,即 \(\mathbf{f} = \frac{R}{2(n - 1)}\):,其中 \(R\) 是镜头表面的曲率半径,\(n\) 是镜头材料的折射率。
径向畸变(Radial Distortion)

上图展示了相机镜头的径向畸变问题,对于穿过镜头边缘的光线,较为容易产生偏差,说明镜头的径向畸变主要是由边缘光线的偏差导致的。同时图像放大率随着与光轴距离的增加而减小。解释了径向畸变对图像放大率的影响规律。
并且,这种畸变主要表现为两种形式:
Pin cushion(枕形畸变):图像边缘向内收缩,形似枕头。
Barrel (fisheye lens)(桶形畸变,鱼眼镜头常见):图像边缘向外凸出,形似桶状。
针孔相机的几何形状(The geometry of pinhole cameras)
在之前的基础上,我们已经把三维空间的点转化到二维平面上了,现在我们需要在二维平面上重新建立坐标系,从而更好地描述图像点的性质。
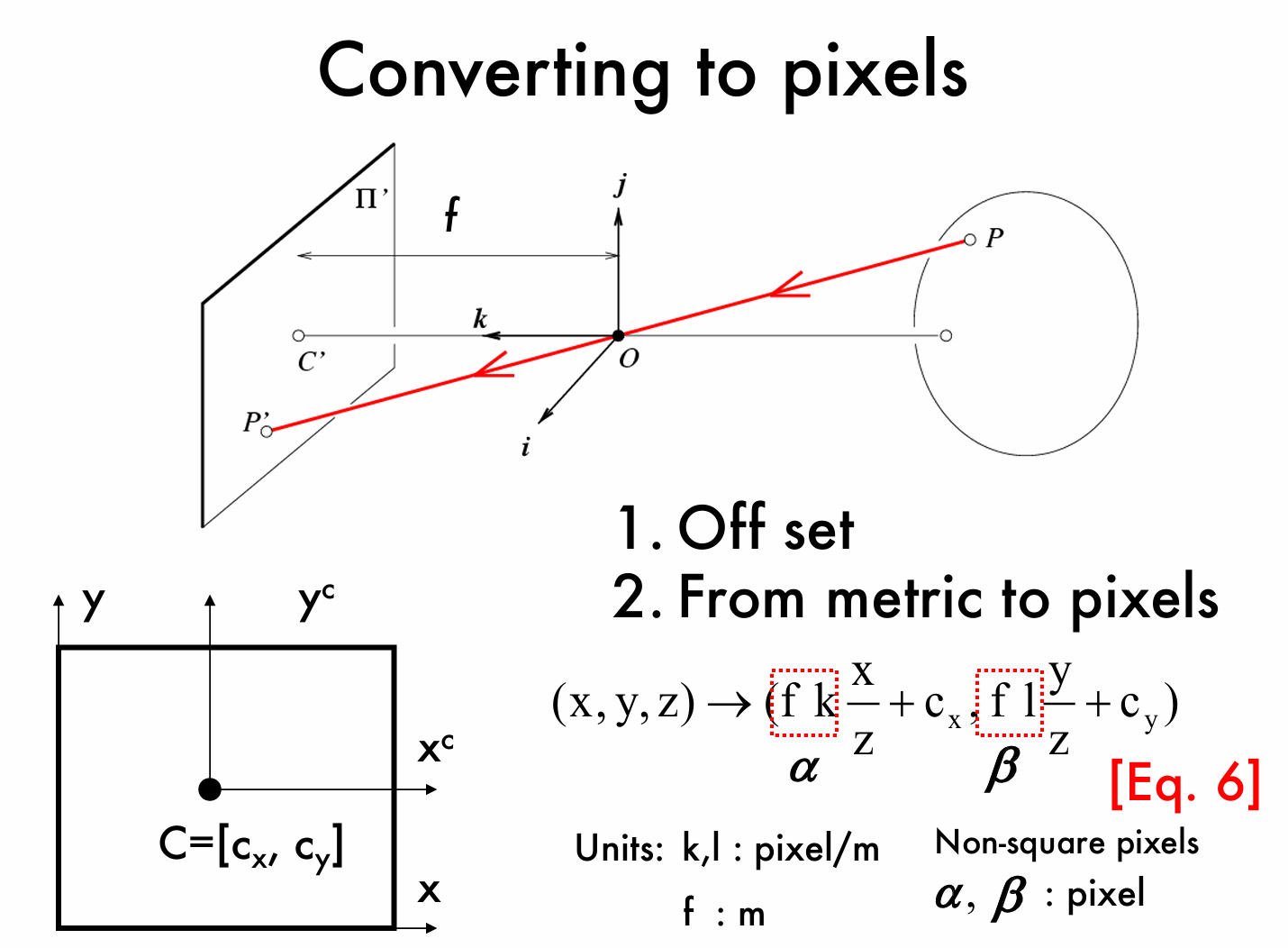
上图展示了将三维点转化为像素点的一般过程:
首先第一步我们需要根据我们在近轴折射模型中介绍的方法,先将三维世界的点转化为二维图像平面的点,然后为了方便我们对于点进行描述,我们需要对坐标进行偏移变换将原来的坐标 \(\begin{cases}x' = f\frac{x}{z} \\ y' = f\frac{y}{z} \end{cases}\) 变换为 \(\begin{cases}x' = f\frac{x}{z}+c_x \\ y' = f\frac{y}{z}+c_y \end{cases}\),其中其中 \(c_x\) 和 \(c_y\) 是偏移量,最后我们需要将单位进行转换,即从度量单位转换为像素单位,从而我们能够在像素平面描述图像点,即 \(\begin{cases}x' = fk\frac{x}{z} \\ y' = fl\frac{y}{z} \end{cases}\) 变换为 \(\begin{cases}x' = fk\frac{x}{z}+c_x \\ y' = fl\frac{y}{z}+c_y \end{cases}\),我们将 \(fk\) 记为 \(\alpha\),将 \(fl\) 记为 \(\beta\),这两个参数的单位都是像素。
我们讨论一下这样的投影变换是线性的吗?显然不是,因为线性变换需满足可加性和齐次性,而此投影变换公式中存在除以 \(z\) 的运算,不满足线性变换的性质,所以该投影变换不是线性变换。
但虽然它不是线性变换,我们依旧能够将他转化为矩阵形式,即通过齐次坐标的方法。
补充一下齐次坐标的相关知识:

对于二维坐标 \((x, y)\) ,转换为齐次图像坐标的形式为 \(\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\) ,对于三维坐标 \((x, y, z)\) ,转换为齐次场景坐标的形式为 \(\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\) 。这表明在齐次坐标系统中,通过在常规坐标的基础上增加一个维度(通常为 1)来表示坐标点。
对于齐次坐标 \(\begin{bmatrix} x \\ y \\ w \end{bmatrix}\) ,转换回二维常规坐标的形式为 \((x/w, y/w)\) ,对于齐次坐标 \(\begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix}\) ,转换回三维常规坐标的形式为 \((x/w, y/w, z/w)\) 。即通过将齐次坐标的每个分量除以最后一个分量 \(w\) ,得到对应的常规坐标。
三维世界中的点的坐标为 \(P_h=(x,y,z)\) ,将其写成齐次坐标的形式,得到 \(P_h=\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\) ,将其投影到图像平面的坐标 \(P_h'=(\alpha \frac xz+c_x,\beta \frac yz+c_y)\) 转化为齐次坐标有 \(P_h'=\begin{bmatrix} \alpha x+c_xz \\ \beta y+c_yz \\ z \end{bmatrix}\),我们惊奇地发现 \(P_h'=\begin{bmatrix} \alpha & 0 & c_x & 0 \\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}P_h\),我们将这个帮助我们实现把三维空间点投影到二维平面的矩阵称为变换矩阵,记作 \(M\)。
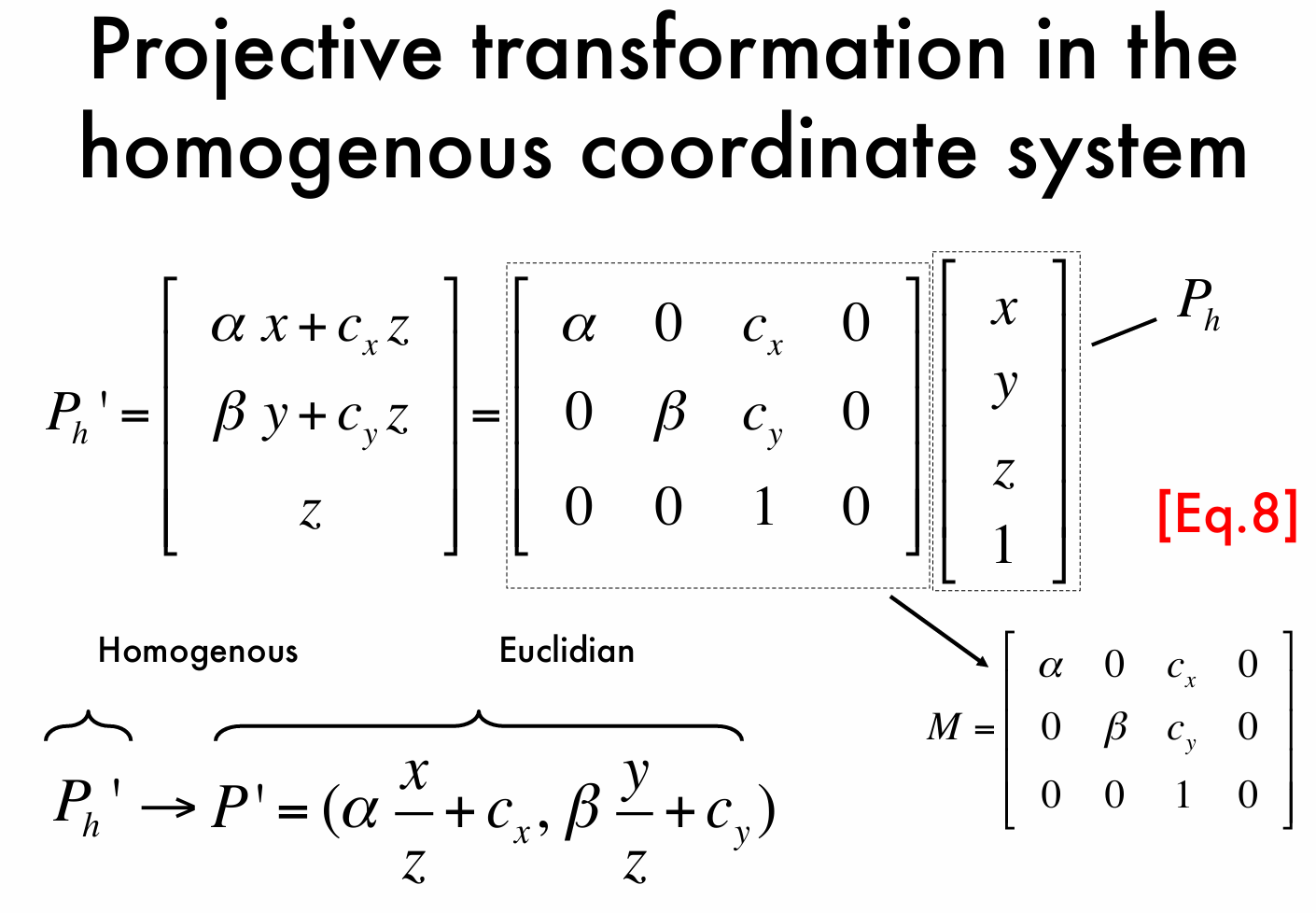
基于以上推导,我们能够得到将三维世界点转化为二维平面点的公式: \(P'=MP\),我们继续观察变换矩阵 \(M\),发现它的最后一列全为 \(0\),因此我们把 \(M\)矩阵的前三列构成的矩阵称为相机矩阵,记为 \(K\),又能把公式写做 \(P'=MP=K[I,0]P\),这里 \(K=\begin{bmatrix} \alpha & 0 & c_x \\ 0 & \beta & c_y \\ 0 & 0 & 1 \end{bmatrix}\)。
但是由于存在相机倾斜的问题,我们需要对变换矩阵 \(M\) 进行修正,修正后的 \(M=\begin{bmatrix} \alpha & -\alpha\cot\theta & c_x & 0 \\ 0 & \frac{\beta}{\sin\theta} & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}\)
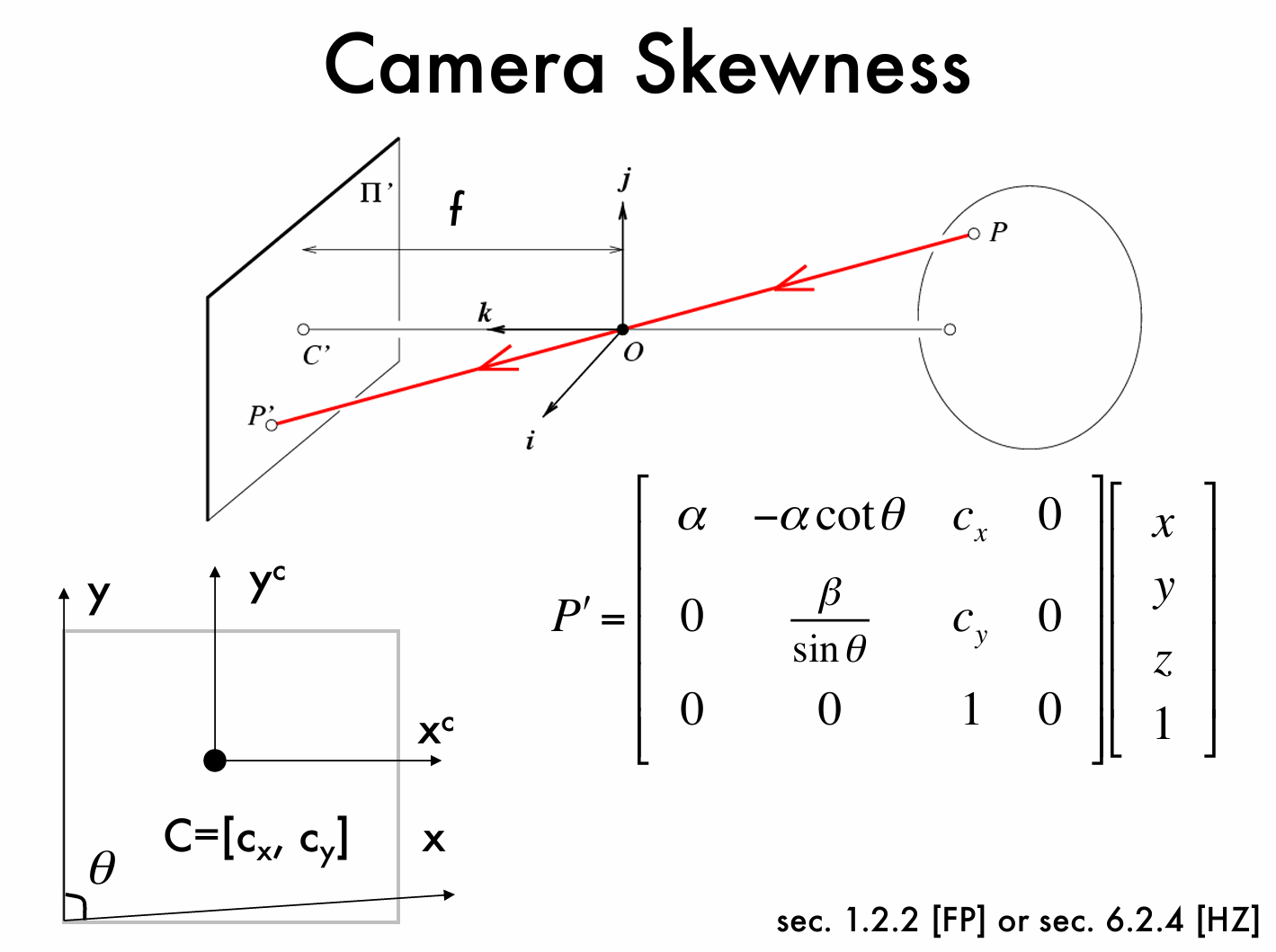
接下来我们分析一下相机矩阵 \(K\) 的自由度,在考虑相机倾斜的情况下, \(\alpha\) 和 \(\beta\) 分别表示在图像平面 \(x\) 和 \(y\) 方向上的缩放因子,这是两个独立的参数,具有两个自由度;\(c_x\) 和 \(c_y\) 分别是图像平面上 \(x\) 和 \(y\) 方向的平移量,即图像中心点的坐标偏移,也是两个独立参数,具有两个自由度; \(\theta\) 表示 \(x\) 和 \(y\) 轴之间的倾斜角度,是一个独立参数,具有一个自由度。综上所述,相机矩阵 \(K\) 共有 \(5\) 个自由度。
最后我们介绍一种投影变换的特殊形式:规范投影变换(Canonical Projective Transformation)。
规范投影变换的矩阵乘法形式为 \(P'=\begin{bmatrix} x \\ y \\ z \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\) ,此变换表示从四维齐次坐标空间 \(\mathbb{R}^4\) 到三维齐次坐标空间 \(\mathbb{R}^3\) 的投影变换(标注为 \(\mathbb{R}^4 \xrightarrow{H} \mathbb{R}^3\) ,这里的 \(H\) 代表齐次坐标变换)。经过变换,我们能够得到投影到二维平面的点坐标,将其转化为非齐次坐标的形式 \(P_i'=\begin{bmatrix} \frac{x}{z} \\ \frac{y}{z} \end{bmatrix}\),说明这是一种非常简单基础的投影变换。
世界参考系(World reference system)
之前讨论的成像等映射关系都是基于相机参考系,那么如果一个物体是在世界参考系中表示的会怎样?此时我们需要引入一个从世界参考系到相机参考系的额外映射。通过旋转和平移变换,将世界参考系下的物体坐标转换到相机参考系中,以便进行后续的成像等处理。
二维平移 (2D Translation)

将 点 \(P\) 移到 \(P'\),有平移方程 \(P' = P + t = (x + t_x, y + t_y)\) 。但是如果我们要用非齐次坐标对它进行表示,我们发现没有办法简单地将平移变换转化为一个矩阵与原来的坐标向量相乘的形式,因此我们考虑齐次坐标,这样平移后的点 \(P'\) 的齐次坐标可通过矩阵乘法得到,即 \(\begin{bmatrix} x + t_x \\ y + t_y \\ 1 \end{bmatrix}=\begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\) ,其中 \(\begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix}\) 为平移变换矩阵 \(T\),平移变换矩阵 \(T\) 也可表示为 \(\begin{bmatrix} I & t \\ 0 & 1 \end{bmatrix}\) ,其中 \(I\) 是 \(2\times2\) 的单位矩阵,\(t=\begin{bmatrix} t_x \\ t_y \end{bmatrix}\) 是平移向量,\(0\) 是 \(1\times2\) 的零向量,\(1\) 是标量。
缩放(Scaling)
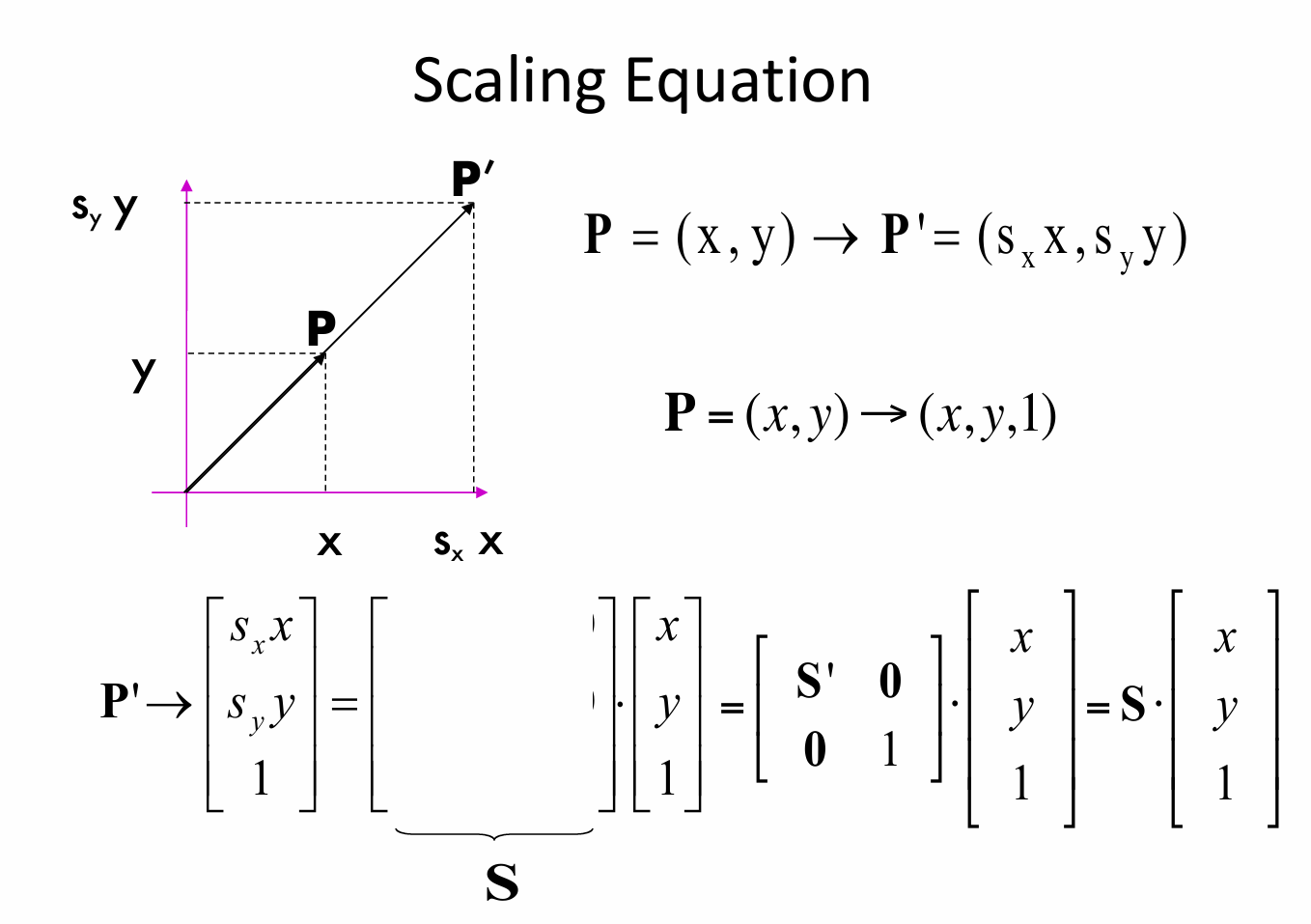
在二维平面中,点 \(P=(x, y)\) 经过缩放变换后,在常规坐标下变为 \(P'=(s_x x, s_y y)\),如果将变换写成齐次坐标的形式,有即 \(\begin{bmatrix} s_x x \\ s_y y \\ 1 \end{bmatrix}=\begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}\) ,其中 \(\begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix}\) 为缩放变换矩阵 \(S\),缩放变换矩阵 \(S\) 也可表示为 \(\begin{bmatrix} S' & 0 \\ 0 & 1 \end{bmatrix}\) ,其中 \(S'=\begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix}\) 是 \(2\times2\) 的缩放子矩阵,\(0\) 分别是 \(2\times1\) 和 \(1\times2\) 的零矩阵,\(1\) 是标量。
旋转(Rotation)
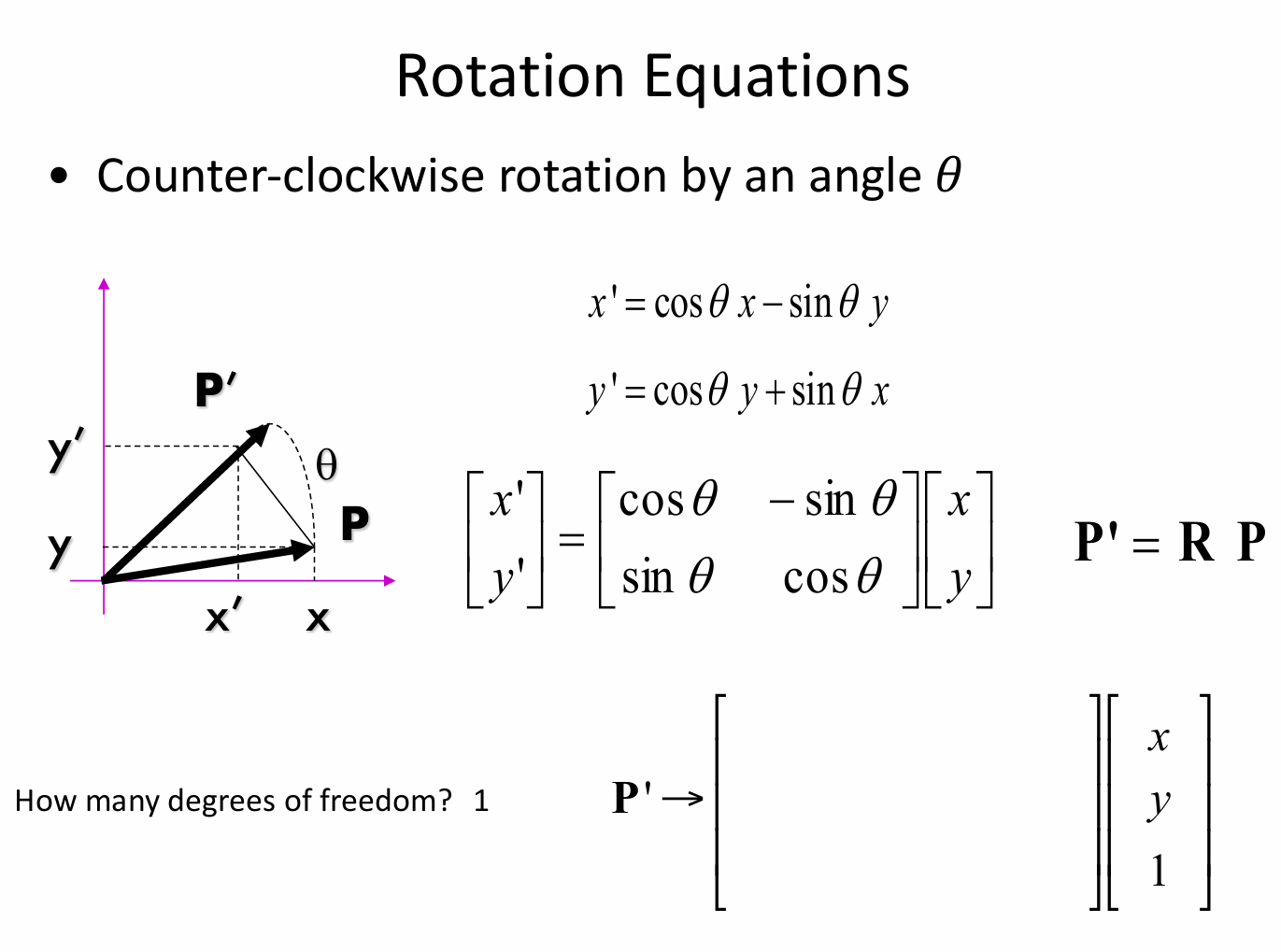
我们这里规定旋转绕原点逆时针旋转角度 \(\theta\),则有坐标变换公式:
\(x' = \cos\theta x-\sin\theta y\)
\(y' = \cos\theta y+\sin\theta x\)
写成矩阵形式:\(\begin{bmatrix} x' \\ y' \end{bmatrix}=\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}\) ,将上述坐标变换公式用矩阵乘法的形式简洁表示,其中 \(\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\) 为旋转矩阵 \(R\) ,即 \(P' = R P\) 。
这个公式的自由度是 \(1\),因为旋转角度 \(\theta\) 是唯一可以自由变化的参数,决定了旋转的具体情况。
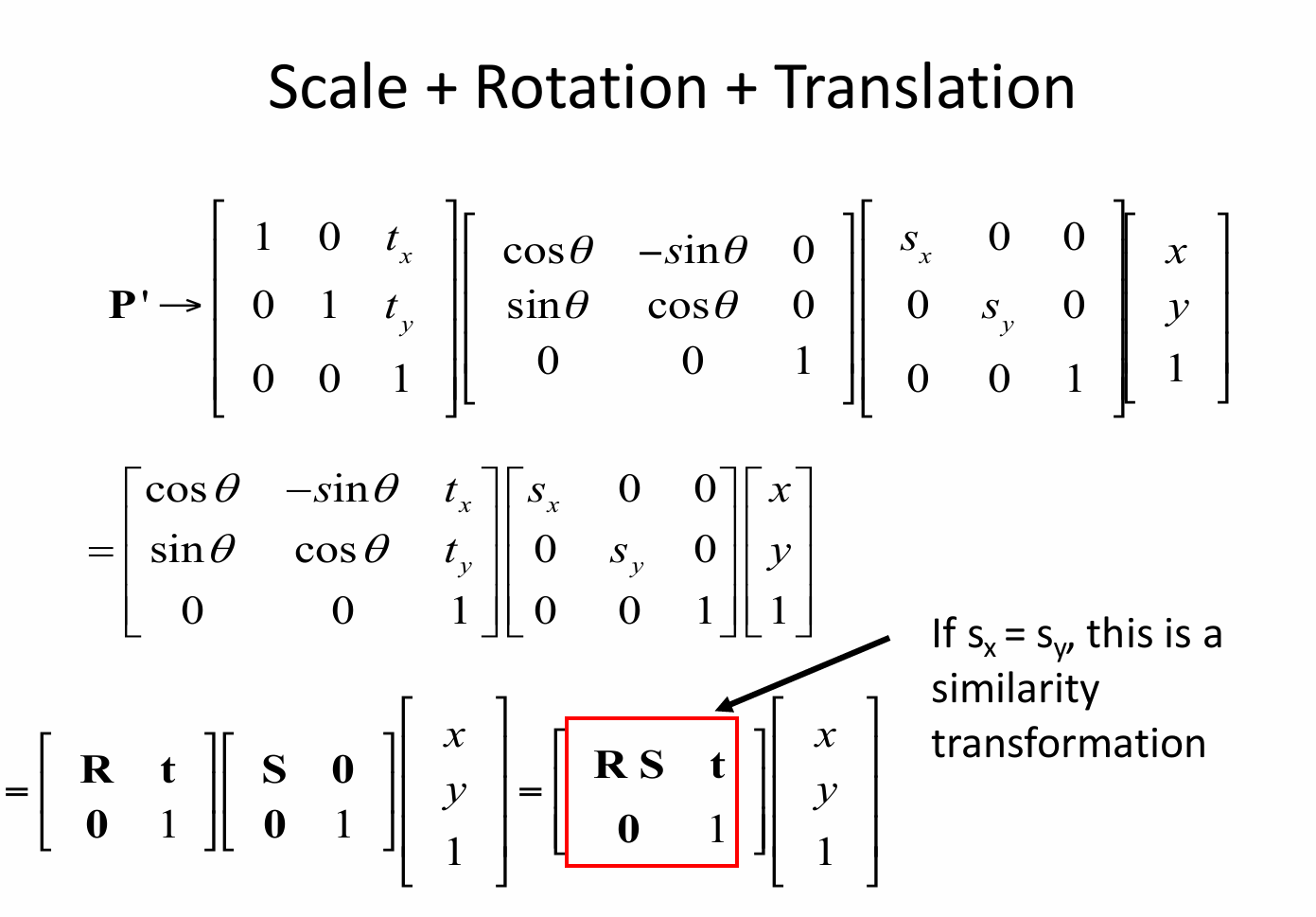
如果我们考虑综合运用这三种变换,我们只需要将三种变换矩阵依次相乘,即如下图所示。特殊的,如果 \(x\) 和 \(y\) 方向的缩放因子相等(\(s_x = s_y\) )时,这种组合变换称为相似变换。相似变换保持图形的形状不变,只改变图形的大小和位置、方向。
接下来我们介绍一下三维变换,相比于二维变换,这里主要讲的是三维变换中的平移和旋转。
三维点的平移(3D Translation of Points)
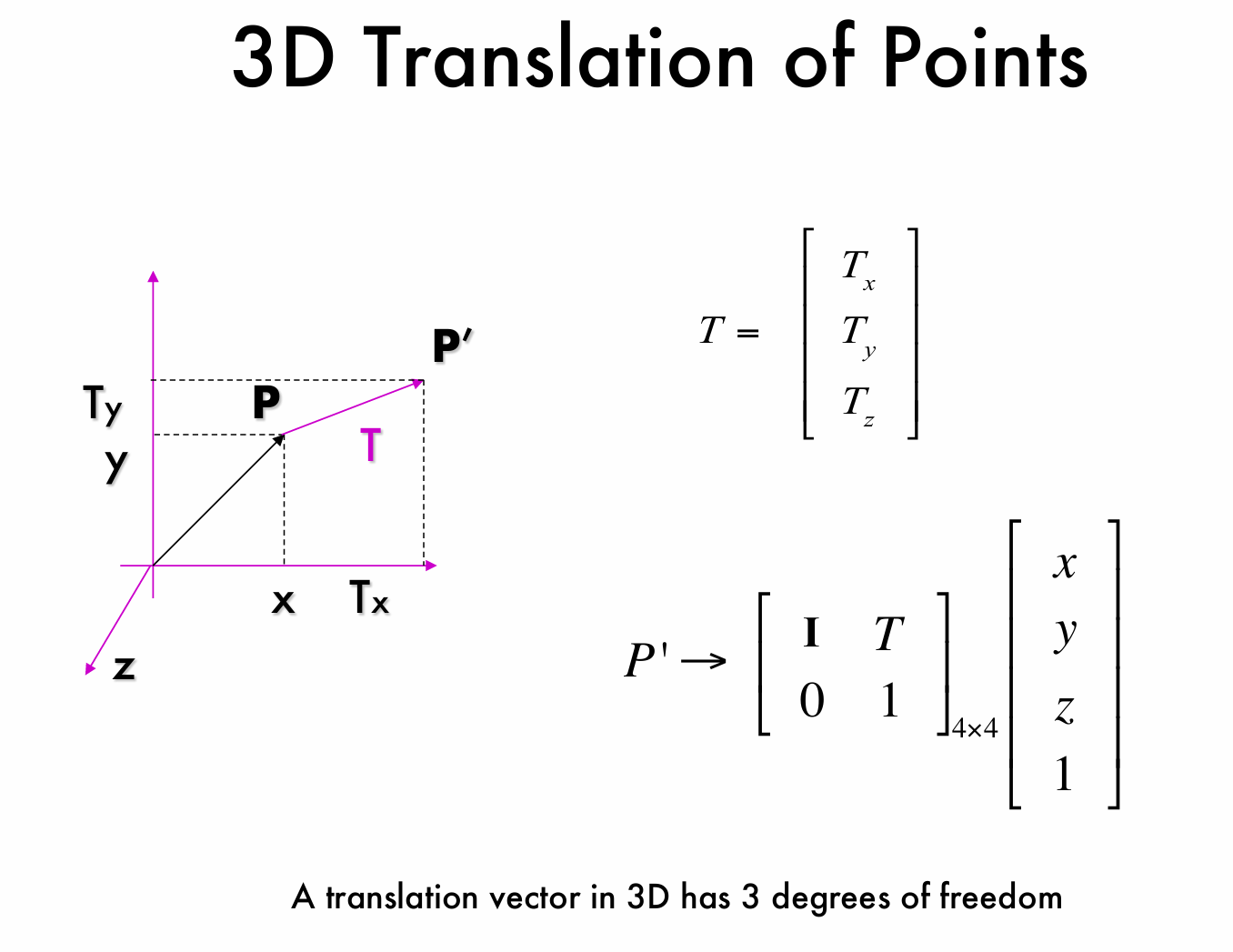
与二维点的平移十分类似,我们可以利用齐次坐标,平移后的点 \(P'\) 的坐标可通过矩阵乘法得到,即 \(P' \to \begin{bmatrix} I & T \\ 0 & 1 \end{bmatrix}_{4\times4} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\) 。
其中 \(\begin{bmatrix} I & T \\ 0 & 1 \end{bmatrix}_{4\times4}\) 是 \(4\times4\) 的平移变换矩阵, \(I\) 是 \(3\times3\) 的单位矩阵, \(T\) 是上述的三维平移向量, \(0\) 是 \(1\times3\) 的零矩阵, \(1\) 是标量。
同时三维平移向量具有 3 个自由度,因为 \(T_x\)、 \(T_y\) 和 \(T_z\) 这三个分量可以独立变化,分别决定了在 \(x\)、 \(y\)、 \(z\) 三个方向上的平移量。
三维点的旋转(3D Rotation of Points)
相比于二维点的旋转,三维点的旋转这里要复杂很多,它由三个旋转矩阵构成:
绕 \(x\) 轴旋转 \(\alpha\) 角度的旋转矩阵 \(R_x(\alpha)=\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha \\ 0 & \sin\alpha & \cos\alpha \end{bmatrix}\) 。
绕 \(y\) 轴旋转 \(\beta\) 角度的旋转矩阵 \(R_y(\beta)=\begin{bmatrix} \cos\beta & 0 & \sin\beta \\ 0 & 1 & 0 \\ -\sin\beta & 0 & \cos\beta \end{bmatrix}\) 。
绕 \(z\) 轴旋转 \(\gamma\) 角度的旋转矩阵 \(R_z(\gamma)=\begin{bmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix}\) 。
依次乘以绕 \(x\)、\(y\)、\(z\) 轴的旋转矩阵得到总的旋转效果,总旋转矩阵为 \(R = R_x(\alpha)R_y(\beta)R_z(\gamma)\) 。
旋转后的点 \(P'\) 的坐标可通过矩阵乘法得到,即 \(P' \to \begin{bmatrix} R & 0 \\ 0 & 1 \end{bmatrix}_{4\times4} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\) 。其中 \(\begin{bmatrix} R & 0 \\ 0 & 1 \end{bmatrix}_{4\times4}\) 是 \(4\times4\) 的变换矩阵, \(R\) 是上述总旋转矩阵, \(0\) 是适当维度的零矩阵, \(1\) 是标量,这种表示利用齐次坐标将三维旋转操作转化为矩阵乘法运算。
三维旋转矩阵也具有 3 个自由度,因为 $ \alpha$ 、$ \beta$ 、$ \gamma$ 这三个旋转角度可以独立变化,分别决定了绕 $ x$ 、$ y$ 、$ z$ 轴的旋转量。

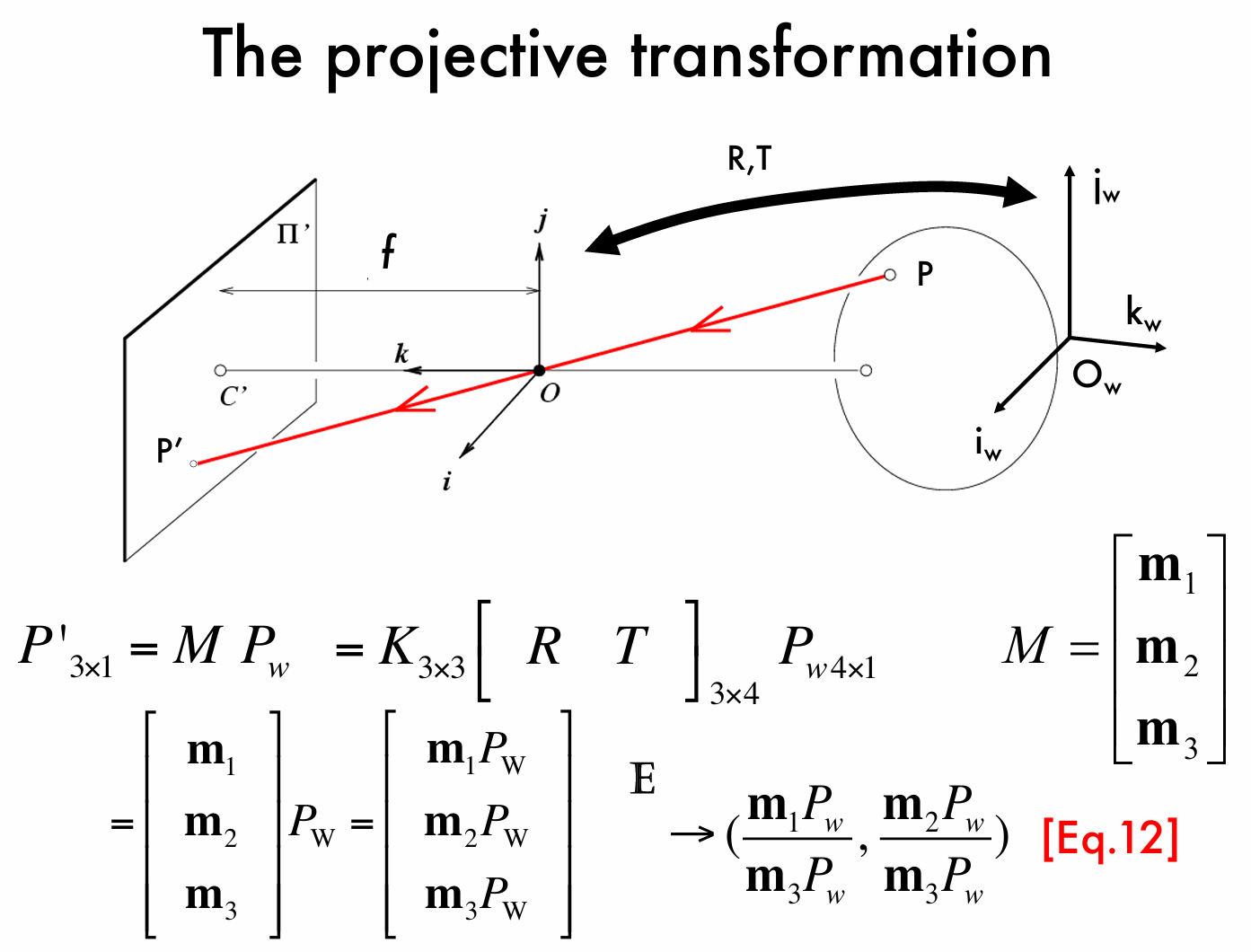
有了这些变换的帮助,我们就能够将世界坐标系下的点转化到相机坐标系:
首先我们将世界参考系下的点 \(P_w=\begin{bmatrix} x_w \\ y_w \\ z_w \\ 1 \end{bmatrix}\) 经过平移旋转变换到相机参考系下的点 \(P\) ,则有 \(P = \begin{bmatrix} R & T \\ 0 & 1 \end{bmatrix}_{4\times4} P_w\),然后我们将其带先前所述的 \(P'=K[I,0]P\),有 \(P'=K[I,0]\begin{bmatrix} R & T \\ 0 & 1 \end{bmatrix}_{4\times4} P_w\),进一步化简得到 \(P'=K[R,T]P_w\),从而展示了从世界参考系下的点 \(P_w\) 到相机成像平面上点 \(P'\) 的完整变换过程。
我们把 \(K\) 叫做相机内参矩阵(Internal parameters),它描述了相机的内部特性,如焦距、主点位置等,把 \([R,T]\) 叫做相机外参矩阵(External parameters) ,它描述了相机在世界参考系中的位置和姿态,由它们组合而成的变换矩阵 \(M\) 共有11个自由度。
如果我们将矩阵 \(M\) 分块进行表示,可分块表示为 \(M = \begin{bmatrix} \mathbf{m}_1 \\ \mathbf{m}_2 \\ \mathbf{m}_3 \end{bmatrix}\) ,投影变换可写成 \(P' = \begin{bmatrix} \mathbf{m}_1 \\ \mathbf{m}_2 \\ \mathbf{m}_3 \end{bmatrix} P_w = \begin{bmatrix} \mathbf{m}_1 P_w \\ \mathbf{m}_2 P_w \\ \mathbf{m}_3 P_w \end{bmatrix}\) 。
从而我们能够得到从齐次坐标到非齐次坐标的转换:通过公式 \((\frac{\mathbf{m}_1 P_w}{\mathbf{m}_3 P_w}, \frac{\mathbf{m}_2 P_w}{\mathbf{m}_3 P_w})\),将齐次坐标形式的 \(P'\) 转换为非齐次坐标形式,也就是实际成像平面上点的坐标表示。
投影变换的属性(Properties of projective transformations)
投影变换主要有三个比较明显的性质:
\(\bullet\) 点投影为点:即在投影变换中,三维空间中的一个点会对应到二维图像平面上的一个点。
\(\bullet\) 线投影为线:意味着三维空间中的一条直线经过投影变换后,在二维图像平面上仍表现为一条直线。
\(\bullet\) 远处的物体看起来更小:这是投影变换的一个直观特性,反映了现实世界中物体的视觉效果,距离观察者越远的物体,在图像中呈现的尺寸越小。
除此之外,投影变换也有着一些比较重要的性质,例如角度不被保留。意思是在投影过程中,三维空间中物体的角度关系在二维投影图像中一般不会保持不变;并且平行线相交! 世界中的平行线在图像中会在一个 “消失点(vanishing point)” 处相交。这是投影的一个重要特性,反映了现实世界在投影到二维平面时的视觉变化。
在下节课我们会围绕这些性质详细展开论述,这部分内容我们就先讲到这里,如有问题,请指正。



![[tldr]通过指令获取github仓库的单个文件的内容](https://img2024.cnblogs.com/blog/3573053/202502/3573053-20250212185738941-1108203471.png)