基环树 DP：学习笔记-编程知识

基环树 DP：学习笔记

news/2025/2/13 19:48:33/文章来源:https://www.cnblogs.com/jerrycyx/p/18714327

总述

定义

基环树，是一个 \(N\) 个点和 \(N\) 条边的连通图，特征是图中有且仅有一个环。特别的，如果不连通且每个连通块的点数和边数都相等，那么这就是一个基环树森林。

基环树 DP，顾名思义，就是在一个基环树上 DP，或是 DP 的结构类似基环树。相对于正常的树型 DP，一般来说基环树 DP 难度更大，代码更加复杂。

处理方法

基环树 DP 一般做的第一件事是找环，方法很多，如拓扑排序等，下面附上我一般用的方法（栈）：

bool vst[N],in_cyc[N];
int sta[N],top;
int cyc[N],cyc_idx;
void Find_cyc(int x,int fa)
{if(vst[x]){cyc[++cyc_idx]=x;in_cyc[x]=true;while(sta[top]!=x){cyc[++cyc_idx]=sta[top];in_cyc[sta[top]]=true;sta[top--]=0;}return;}vst[x]=true;sta[++top]=x;for(int i=head[x];i;i=edge[i].nxt){int y=edge[i].to;if(y==fa) continue;Find_cyc(y,x);if(in_cyc[y]) break;}sta[top--]=x;return;
}

基环树 DP 由于其比正常树多了一条边的特性，可以用以下两个视角看待：

一棵树和一条额外边

把基环树看作一棵树和一条额外的边（横叉边或后向边都有可能），在处理的时候像正常的树一样跑树型 DP，在额外边所连接的两点处做特判等特殊处理。

在这个视角下，基环树长这样：

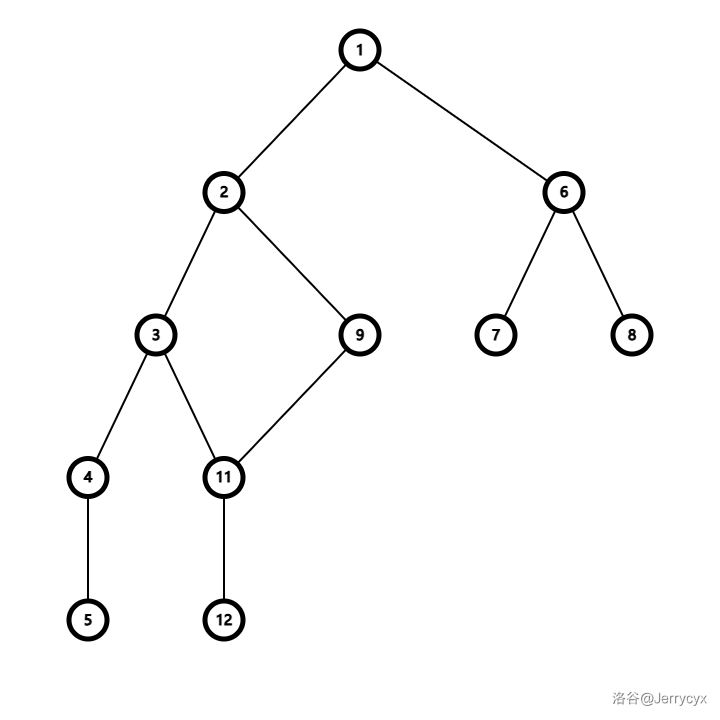
一个广义“根节点”和若干子树

把基环树的环看作一个广义的“根节点”，许多子树挂在这个环上。环上每个点都可以作为一个单独的根节点计算出各自子树的答案，最后再对整个环统一进行计算。

在这个视角下，一般会把基环树画成这样一个形态：

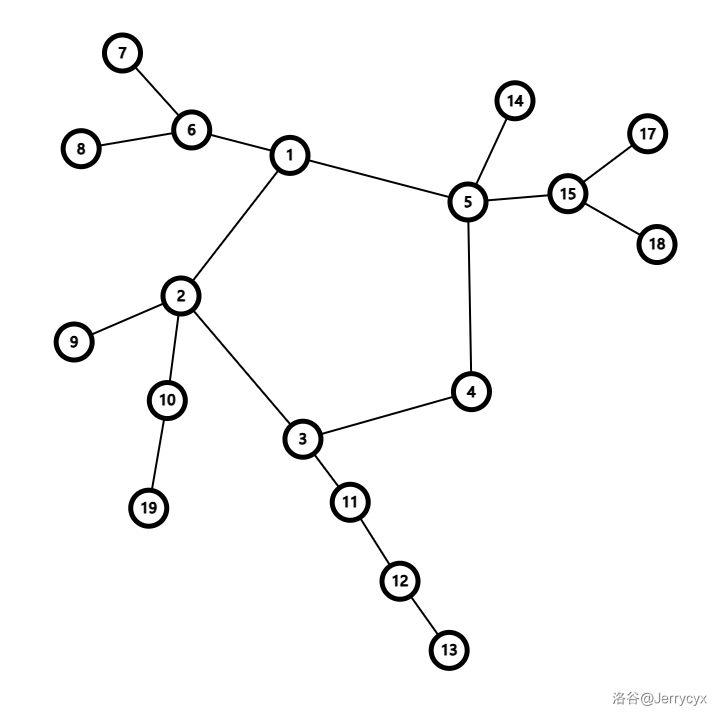
（是哪个天才说长得像细菌的？）

或者把环压平，像这样：

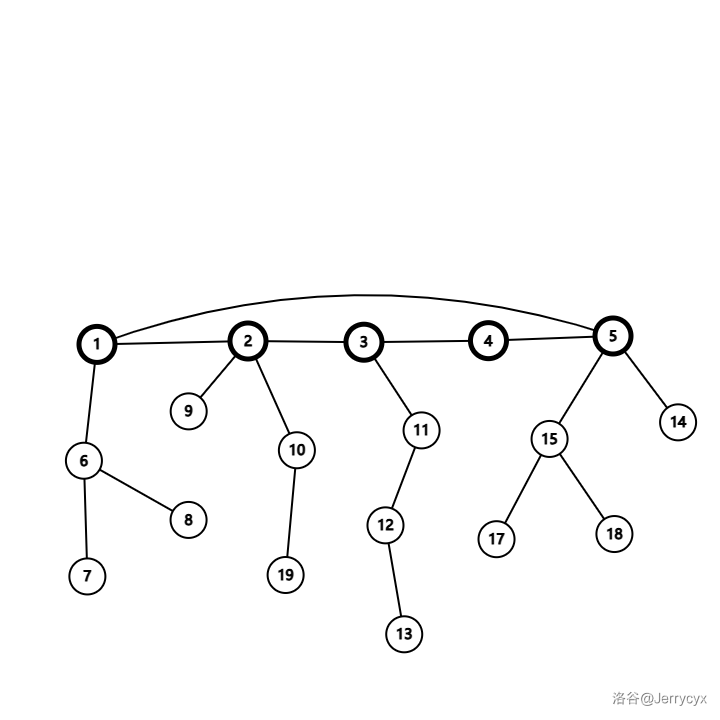
例题

P1453 城市环路

简化题意：求树上带权最大独立集（其中任意两点都没有边相连）

分别考虑用两种视角来做这道题：

视角#1：树带额外边

容易发现如果没有环，这道题和没有上司的舞会一模一样，而这条额外边只是多了一条限制而已。

首先直接遍历树，找到这条额外边所连接的两点，设其为 \(x\) 和 \(y\)。

强制 \(x\) 不能选，跑一遍普通树型 DP）；再强制 \(y\) 不能选，跑一遍普通树型 DP。两次 DP 取最大值即为答案，因为这样保证了 \(x\) 和 \(y\) 至少有一个没有选，所以不可能两个都选。

视角#2：环带若干子树

首先找出环，对环挂着的每一个子树单独跑一边树型 DP，求出根节点选或不选时的最大价值。

然后对环上所有点跑环状 DP。具体来说，设 \(f_{0/1,i,0/1}\) 表示第一个点选/不选且第 \(i\) 个点选/不选时，前 \(i\) 个点的最大价值。答案即为 \(\max\{f_{0,c,0},f_{0,c,1},f_{1,c,0}\}\)（\(c\) 表示环上点数），同样保证了第 \(1\) 个点和第 \(c\) 个点不能同时选。

（其实从本质上看，这两种方法是一样的。）

P4381 [IOI 2008] Island

简化题意：求基环树的直径。

基环树的直径定义为：树上最长链的长度。

这个题似乎只能用视角二。

把基环树上路径分成两种，不经过环的和经过环的。

不经过环的直接就是正常求树的直径，随便写写就行。

经过环的分为三段：从一棵子树开始，环上走一段，在另一棵子树结束。

预处理出每棵子树的高度 \(h_i\)，然后答案就是：

\[\max_{i \neq j}\{ h_i+h_j+dis(i,j) \} \]

前缀和搞一下可以转成：

\[\max_{i<j}\{h_i+h_j+dis_j-dis_i\} = \max_{i<j}\{h_i-dis_i + h_j+dis_j\} \]

然后有两种方法处理环上求解上述式子，这两种都建议掌握，特别是后一种虽然比较麻烦但是更为通用。

法一：拆分两种路径

同时因为环上两点间有两条路径，所以还要反过来更新一下答案（\(L\) 表示环总长）：

\[\max_{i<j}\{h_i+h_j+L-(dis_j-dis_i)\} = L+ \max_{i<j}\{h_i+dis_i + h_j-dis_j\} \]

两部分分别算一下，取个最大值就是答案。

法二：单调队列限制距离

把环从某处断开，复制一份接到末尾，这条新链上任意一条点数不超过原环点数的子区间都可以表示原环上的一段距离。

然后我们可以枚举 \(j\)。不断右移 \(j\) 的过程中 \(h_j+dis_j\) 确定，通过单调队列找到定长区间 \([j-s+1,j)\)（\(s\) 表示原环点数）内最大的 \(h_i-dis_i\)。两者相加即可更新答案。

P1399 [NOI2013] 快餐店

~~其实我觉得这应该是个紫题的~~

点名表扬这篇题解，把这道题所需结论讲正确且讲清楚了。引用一下：

我们做出答案点的最短路生成树，发现答案点也是该生成树上到其它点距离的最大值最小的点（对于该生成树的答案），于是可以考虑枚举生成树并求生成树的答案。接着又发现枚举生成树求出的答案值不会小于原图的答案值，于是算法正确性成立。

结论：本题答案为删去环上任意一条边后所得树直径的最小值的一般。不是基环树直径的一半！

本题仍然使用视角二。

虽然不能求基环树直径，但是仍然需要先找环，算出每个子树各自的直径和深度。

首先这些直径是无论如何切环都不会变的，设其中的最大值为 \(mxsub\)。然后假定环上有 \(k\) 个点，且以 \(1,2,3,\dots k\) 的顺序排列，设各个子树的深度为 \(h_i\)。

接着可以发现，上述法二刚好满足我们的需求：其框定的一块长度为 \(k\) 的区域恰好就相当于将环从区域两端点处断开。那么我们根据之前的结论可得此时答案应该是为：

\[\max_{l \le i<j \le l+k-1}\{(h_i-dis_i) + (h_j+dis_j)\} \]

而我们要在均摊 \(O(1)\) 的时间复杂度下求解这个，容易想到两个单调队列分别维护 \(h_i-dis_i\) 和 \(h_j+dis_j\) 的值。然后你就会发现：这种做法无法判断 \(i \neq j\)。

一般在这种情况下，常用的处理方法都是记录一个次大值以作备用，但是很快你就会愤怒地发现：单调队列不！能！维！护！次大值（大佬们如果知道方法麻烦告诉我一声，感激不尽）。

上面提到的题解里也发现了这个问题，他使用了一种变异的单调队列，其实是将在线转为了离线处理（普通单调队列是在线的）。本蒟蒻爆调 \(4\) 小时未能战胜，最终放弃转而采用温柔体贴的线段树，\(25\) 行就解决了，甚至比那个变异单调队列还短。

（然后这就引申处一个结论：维护次大值的时候，只有不重合的区间才可以直接合并。所以理论上 ST 表也不能直接这样求解次大值）

记每种切法（即每段区间）这样得到的答案的最小值为 \(ans\)，总答案即为 \(\max(mxsub,ans)\)。

代码在下面，有空可以参考以下，没空就算了。

#include<cstdio>
#include<algorithm>
#define LL long long
using namespace std;const int N=1e5+5;
int n;struct Allan{int to,nxt;int val;
}edge[N<<1];
int head[N],idx;
inline void add(int x,int y,int z)
{edge[++idx]={y,head[x],z};head[x]=idx;return;
}bool vst[N],in_cyc[N];
pair<int,int> sta[N]; int top;
pair<int,int> cyc[N]; int cyc_idx;
void Find_cyc(int x,int fa)
{if(vst[x]){cyc[++cyc_idx]={x,0};in_cyc[x]=true;while(sta[top].first!=x){cyc[++cyc_idx]=sta[top];in_cyc[sta[top].first]=true;top--;}cyc[1].second=sta[top].second;reverse(cyc+1,cyc+cyc_idx+1);return;}vst[x]=true;sta[++top]={x,0};for(int i=head[x];i;i=edge[i].nxt){int y=edge[i].to,z=edge[i].val;if(y==fa) continue;sta[top].second=z;Find_cyc(y,x);if(in_cyc[y]) break;}top--;return;
}LL mxdep[N],diam[N];
void Calc_diam(int x,int fa)
{for(int i=head[x];i;i=edge[i].nxt){int y=edge[i].to,z=edge[i].val;if(y==fa || in_cyc[y]) continue;Calc_diam(y,x);diam[x]=max({diam[x],diam[y],mxdep[x]+mxdep[y]+z});mxdep[x]=max(mxdep[x],mxdep[y]+z);}return;
}inline void updsec(pair<LL,int> &src1,pair<LL,int> &src2,pair<LL,int> t)
{if(t>src1) src2=src1,src1=t;else if(t>src2) src2=t;return;
}struct SegmentTree{int l,r;pair<LL,int> dat[2];
}tree[2][N<<3];
inline SegmentTree merge(SegmentTree ls,SegmentTree rs)
{SegmentTree res;res.l=ls.l,res.r=rs.r;res.dat[0]=ls.dat[0],res.dat[1]=ls.dat[1];updsec(res.dat[0],res.dat[1],rs.dat[0]);updsec(res.dat[0],res.dat[1],rs.dat[1]);return res;
}
void Build(bool op,int p,int l,int r,LL src[])
{tree[op][p].l=l,tree[op][p].r=r;if(l==r){tree[op][p].dat[0]={src[l],l};tree[op][p].dat[1]={-1e18,0};return;}int mid=l+r>>1;Build(op,p<<1,l,mid,src);Build(op,p<<1|1,mid+1,r,src);tree[op][p]=merge(tree[op][p<<1],tree[op][p<<1|1]);return;
}
SegmentTree Query(int op,int p,int l,int r)
{if(l<=tree[op][p].l&&tree[op][p].r<=r)return tree[op][p];int mid=tree[op][p].l+tree[op][p].r>>1;SegmentTree res;if(l<=mid&&r>mid) return merge(Query(op,p<<1,l,r),Query(op,p<<1|1,l,r));else if(l<=mid) return Query(op,p<<1,l,r);else return Query(op,p<<1|1,l,r);
}LL ans=1e18;
LL s[N<<1],d[N<<1],a[N<<1],b[N<<1];
void Main_Solve()
{LL mxsub=0;for(int i=1;i<=cyc_idx;i++){mxsub=max(mxsub,diam[cyc[i].first]);s[i]=mxdep[cyc[i].first];d[i]=cyc[i].second;}for(int i=1;i<cyc_idx;i++)s[cyc_idx+i]=s[i],d[cyc_idx+i]=d[i];for(int i=1;i<cyc_idx<<1;i++){d[i]+=d[i-1];a[i]=s[i]+d[i-1],b[i]=s[i]-d[i-1];}Build(0,1,1,(cyc_idx<<1)-1,a);Build(1,1,1,(cyc_idx<<1)-1,b);for(int i=1;i<=cyc_idx;i++){int l=i,r=i+cyc_idx-1;SegmentTree tmpa=Query(0,1,l,r),tmpb=Query(1,1,l,r);LL tot=tmpa.dat[0].second==tmpb.dat[0].second?max(tmpa.dat[0].first+tmpb.dat[1].first,tmpa.dat[1].first+tmpb.dat[0].first):tmpa.dat[0].first+tmpb.dat[0].first;ans=min(ans,tot);}ans=max(ans,mxsub);return;
}int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){int x,y,z; scanf("%d%d%d",&x,&y,&z);add(x,y,z),add(y,x,z);}Find_cyc(1,0);for(int i=1;i<=cyc_idx;i++)Calc_diam(cyc[i].first,0);Main_Solve();printf("%.1lf\n",ans/2.0);return 0;
}

顺便给个双倍经验。