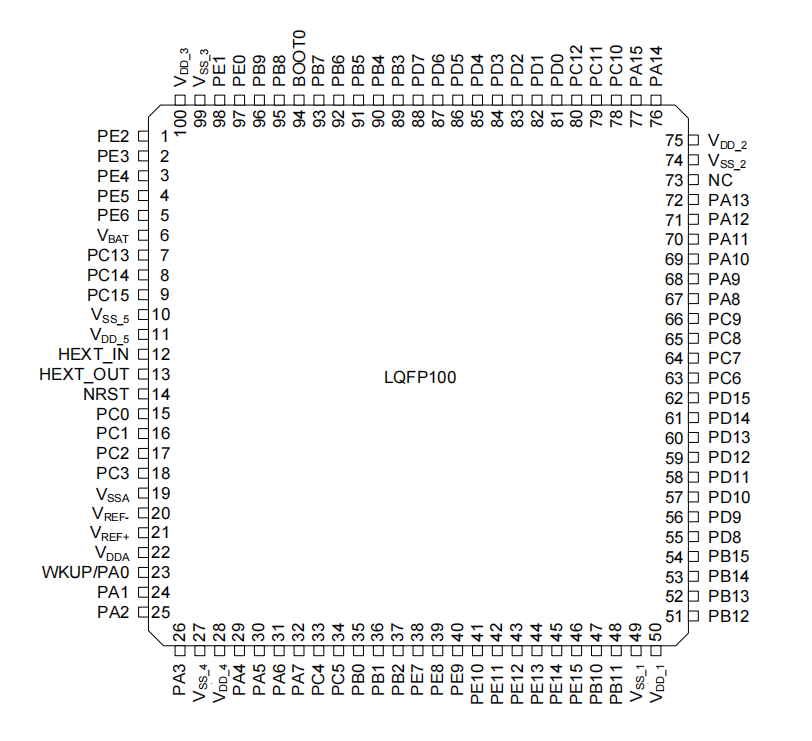
普朗克能量子
定义
普朗克认为,带电微粒(高中阶段主要研究电子)辐射或吸收能量的时候,只能辐射或吸收某个最小能量值的整数倍。这个不可再分的最小能量值就叫做能量子。
通常的,我们认为光子也是一种能量子。
能量子大小
公式:
其中,$$ε$$ 代表该能量子的能量大小,
$$ν$$ 代表电磁波的频率,
$$h$$ 代表普朗克常量,大小约是
光电效应
任何照射到金属表面的电磁波,能量被该金属表面电子吸收后,导致电子逸出的现象,称为光电效应,逸出的电子称为光电子。
实验规律
-
任何一种金属都有一个截止频率 \(ν_c\) ,入射光的频率必须大于该截止频率才能产生光电效应。若小于截止频率,则无论光强多强都不会产生光电效应。
-
入射光照射到金属上是,光电子的发射几乎是瞬时的,一般不会超过 \(10^{-9}s\) 。
重要概念
逸出功
逸出功( \(W_0\) ) 是使电子能够脱离某种金属所需的最小能量(最小做功),逸出功决定了截止频率。
光电子最大初动能
发生光电效应后,金属表面电子吸收光子后克服原子核引力逸出时,所具有的最大的动能。
爱因斯坦光电效应方程
表达式:$$E_k=hν-W_0$$
该方程表明,光电子的最大初动能与入射光的频率 \(ν\) 呈现线性关系而非正比,与光强无关。
其物理意义是:一个电子吸收光子能量后,一部分克服金属逸出功 \(W_0\) ,另一部分则变成逸出后的最大初动能。
饱和光电流

如图,向该光电管加正向电压,则随着正向电压的增大,光电流会趋向于一个饱和值,也就是在电流较小时,电流随电压增大而增大,但当电流增大到一定值,无论如何提高电压,电流都不会增大了。
产生这种现象的原因是在光强一定的情况下,光电子的供应量是有限的,就像是学校放学,学生出校门的速度是 \(100人/分钟\) ,当校门很小时,这个速度会被减小,随着校门扩大,速度逐渐提升,但是当校门扩大到一定程度,无论如何扩大都会维持在这个速度。
饱和光电流的重要前提条件:光照条件不变!
遏止电压

如图,对光电管加反向电压,在某光照环境下使得光电流正好减为零,该电压称为遏止电压( \(U_c\) )。
公式如下:$$eU_c=E_k=hν-W_0$$
其中,\(e\) 指的是电子的带电荷量。
饱和光电流、遏止电压的动态分析
光强的公式:$$I=n·hν$$
\(n\) 代表光子数目。
颜色相同、强度不同的光
他们的遏止电压相同,因为频率相同。
强光的饱和光电流大,弱光的饱和光电流小,因为光子数目减少。
颜色不同、强度相同的光
高频光的遏止电压高,饱和光电流低,
低频光的遏止电压低,饱和光电流高。
原因:光照强度相同,高频光频率高则光子数目少,而饱和光电流与光子数目有关,与频率无关。