线性基学习笔记
概述
对于一组 \(n\) 维向量张成的空间,存在一组向量能线性表示出这个空间中的所有向量,向量个数最少的向量组构成一组基底。
线性代数中,我们知道:向量排列在行上,进行消元能得到一组基,排在列上,消元能得到极大线性无关组(也是一组基)。在布尔空间中,用异或运算表示 01 向量的线性变换。
异或线性基可以解决许多问题,例如:
- 求出一组基底,极大线性无关组。
- 计算一组数选择若干异或起来的最值,第 \(k\) 大值。
- 判断一个数能否被给定的一些数异或出来,并给出方案。
构造
同线性代数,我们可以直接进行高斯消元求出线性基,对于 \(n\) 个 \(m\) 维的向量,复杂度为 \(O(nm^2)\),其中包含一个位运算的复杂度,\(m\) 很小时位运算是 \(O(1)\) 的,复杂度是 \(O(nm)\),\(m\) 较大时可以用 bitset 优化成 \(O(\frac{nm^2}{w})\)。
我们还可以贪心构造线性基,代码量小,常数比消元法小。
我们需要构造的基地满足:每个基向量的二进制最高位均不相同。由此设 \(a_i\) 为二进制最高位为 \(i\) 位的基向量是什么。插入一个向量时,从高位到低位枚举,若第 \(i\) 位存在基向量且该向量第 \(i\) 位为 \(1\),那么这一位就可以被表示出来,异或掉这一位,直到存在某一位还没有基向量,且插入向量这一位为 \(1\) ,则该向量就可以占领这一位,构成一个基向量。若插入向量最终异或到 \(0\) 了,那该向量可以被线性表示,不加入基向量。
查询某向量能否被线性表示,只需要遍历线性基判断即可,过程和插入类似。
在异或的过程中,我们记录每一个基向量是被哪些向量异或出来的,查询时记录方案即可。
bool insert(int x)
{for(int i=m;i>=0;i--){if(x>>i&1){if(a[i]>>i&1) x^=a[i];else {a[i]=x; return 1;}}}return 0;
}
性质
高斯消元构造的线性基,是行简化阶梯型,但贪心法构造的不是,下面两个例子来说明这一点(左边为消元法,右边为贪心法,重点看 \(1,2,4\) 主元列):
即,主元列上只有一个向量这一位是 \(1\) 。
简化阶梯型是个很好的性质,为了在贪心法中得到简化阶梯型,可以在最后得到的基底中再执行一次消元,把主元列多余的 \(1\) 消掉,得到行简化阶梯型。
应用
以下的应用基于满足行简化阶梯型的基底。
- 异或最值,第 \(k\) 大
最小值:若某向量能被线性表示则为 \(0\) ,否则为最低位基向量。
最大值:由于每个最高位唯一,直接把基向量全部异或起来就行。
第 \(k\) 大:主元列是唯一的,假设基底有 \(n\) 个基向量,那能得到 \(2^n\) 个值,根据高位贪心,把 \(k\) 二进制拆分,选择二进制为 \(1\) 的基向量异或起来。
例题
Extracting Weights
- 题意
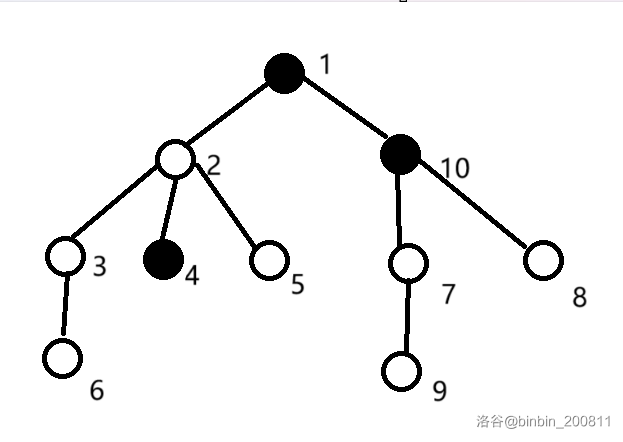
给一棵树,每个点有一个权值 \(w_i\),根节点 \(w_1=0\),最多进行 \(n\) 次询问,每次询问两点间所有点的异或值,询问要保证两点间的路径长度恰好为 \(k\),能否求出所有点的权值,如果能,和交互库交互求出权值。\(n \leq 250\)
- 题解
任意 \(n\) 个线性无关的方程组就能解出每个点的权值,其中包含 \(w_1=0\) 的方程。枚举两端点,找出方程组就行,判断线性无关用 bitset 维护线性基,复杂度 \(O(\frac{n^4}{w}+n^3)\)。
注意要提前插入 \(w_1=0\) 这个方程。