2.22总结反思

2.22总结&反思

联合省选2024Day1T1补题

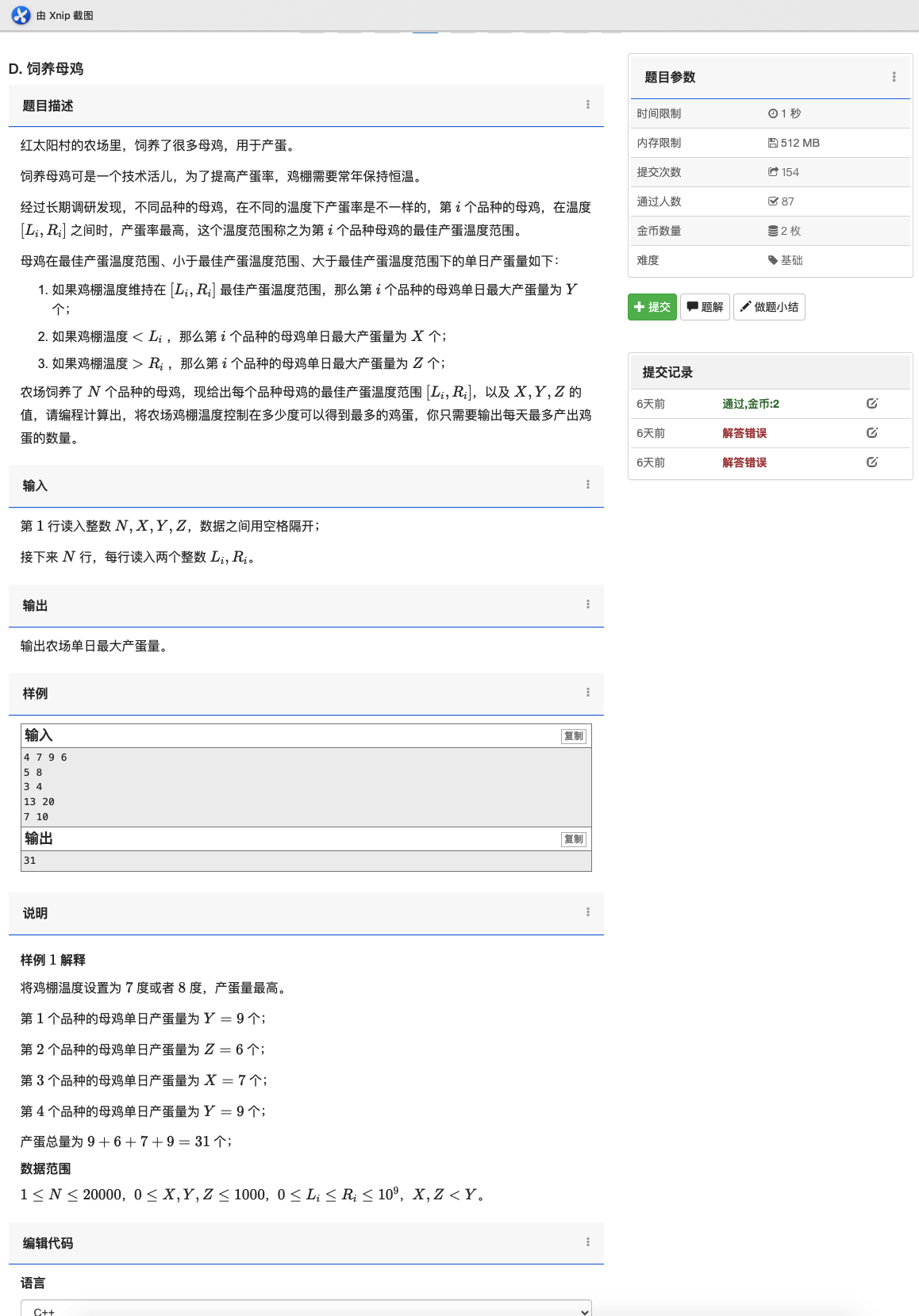
很有意思的题目，欣喜的是独立做出来了，虽然洛谷标的难度为蓝，但其实仔细一想并不困难，大致分为三步，每一步想法基本都是普及水平：

1. 想出对于特定的\(m\)如何进行简便的构造
2. 列出方程之后观察式子想好枚举什么对象（本题为模\(n\)下的值）
3. 对于每类，列出不等式即可

想法很自然，困难地方为解不等式时的细节，注意代码中的绝对值分讨，不等式变号，判0情况以及\(INF\)要开到\(10^{18}\)。

启发：

不要怕题面的复杂，一步一步自然地想做法。一定要先想出完整想法和所有情况再写代码，慢想法，快代码，不然导致细节处调代码时间很长。

摩尔投票

很好的一个小trick，对于求一个可重集合中出现次数严格大于一半的数（绝对众数）很有用，可以把每类数分为一个集合，绝对众数是最大的一个集合，如果不同集合间的数分别两两抵消，则剩下来的一定是绝对众数（可以考虑最坏情况证明），有如下性质和扩展：

• 具有结合率，故可以采用线段树维护来实现区间操作
• 可以扩展到求出现次数严格大于三分之一等等的数

云斗模拟赛round1day1T2

太绝望了，我不会。

看题解！

二分\(m\),考虑大于小于的化1和0，考虑最多可以选多少数（后判断子序列长度大小比较），所有1必选（有不选1的情况可以转换）。

考虑\(m\)增大，0化为1，考虑增多的贡献如何，然后考虑\(m\)在哪个范围可产生新贡献。

啊啊啊11点了该睡了，剩下貌似是整体二分然后推到可持久化线段树。

额额，没看完，就睡了吧，兴许在床上有基础思路后可以顺利推出😊

剩下的明天再来探索吧😋

总结

呃呃，干实事，别内耗。

做题考虑学习思考过程内化，而不是单纯知道方法，把看起来的不自然的化为自然的。