SARSA算法
SARSA(State - Action - Reward - State - Action)算法和Q - learning算法均为强化学习领域中用于学习最优策略的无模型算法,二者存在诸多区别,下面从多个方面进行详细阐述: ### 算法类型与策略特性 - **离线策略与在线策略** - **Q - learning**:属于离线策略(off - policy)算法。这意味着在学习过程中,用于生成动作数据的行为策略(通常是 $\epsilon$-贪心策略,以一定概率 $\epsilon$ 随机选择动作进行探索,以 $1 - \epsilon$ 的概率选择Q值最大的动作进行利用)和用于更新Q值的目标策略(贪心策略,即总是选择Q值最大的动作)是不同的。这种特性使得Q - learning可以直接学习到最优策略,即使行为策略是随机探索的。 - **SARSA**:是在线策略(on - policy)算法。在学习过程中,行为策略和目标策略是相同的,一般都采用 $\epsilon$-贪心策略。这使得SARSA更加保守,因为它会考虑到在探索过程中实际采取的动作带来的后果。 ### 更新公式 - **更新公式的形式** - **Q - learning**:其核心是对Q值函数进行迭代更新,更新公式为 $$Q(s,a) \leftarrow Q(s,a)+\alpha\left[r + \gamma\max_{a'}Q(s',a')-Q(s,a)\right]$$ 其中,$s$ 表示当前状态,$a$ 是当前采取的动作,$r$ 是执行动作 $a$ 后获得的即时奖励,$s'$ 是转移到的下一个状态,$\alpha$ 是学习率,控制每次更新的步长,$\gamma$ 是折扣因子,体现了对未来奖励的重视程度。$\max_{a'}Q(s',a')$ 表示在下一个状态 $s'$ 下,所有可能动作 $a'$ 对应的Q值中的最大值。这表明Q - learning在更新时总是朝着最优动作的方向进行,具有贪心的特性。 - **SARSA**:更新公式为 $$Q(s,a) \leftarrow Q(s,a)+\alpha\left[r + \gamma Q(s',a')-Q(s,a)\right]$$ 这里的 $a'$ 是在状态 $s'$ 下根据当前策略($\epsilon$-贪心策略)实际选择的动作。与Q - learning不同,SARSA使用的是实际执行的动作 $a'$ 对应的Q值 $Q(s',a')$ 来更新当前状态 - 动作对 $(s,a)$ 的Q值。 ### 探索与利用的平衡 - **对探索的处理** - **Q - learning**:由于其离线策略的特性,在探索过程中,即使采取了一些随机动作,也会尝试朝着最优策略的方向更新Q值。这可能导致在某些情况下,它会更激进地去探索可能的最优路径,甚至可能会走入一些危险区域(在环境中存在风险的情况下),因为它总是期望找到全局最优解。 - **SARSA**:在线策略使得它会更加谨慎地对待探索。因为它的更新是基于实际执行的动作序列,所以在遇到一些可能有风险的动作时,会通过更新Q值来避免再次选择类似的动作,从而表现得更加保守。 ### 收敛性与稳定性 - **收敛特性** - **Q - learning**:在一定条件下可以收敛到最优的Q值函数 $Q^*(s,a)$,从而得到最优策略。但由于其贪心更新的特点,在某些复杂环境中可能会出现收敛速度较慢或者陷入局部最优的情况。 - **SARSA**:同样在满足一定条件下可以收敛,但由于它考虑了实际执行的动作,其收敛过程相对更加稳定,对环境中的噪声和不确定性有一定的鲁棒性。不过,它收敛到的可能不是严格意义上的最优策略,而是与当前采用的策略(如 $\epsilon$-贪心策略)相关的一个较好的策略。 ### 适用场景 - **不同场景的适应性** - **Q - learning**:适用于环境相对稳定、奖励机制明确,且希望快速收敛到最优策略的场景。例如在一些棋盘游戏、确定性的路径规划问题中,Q - learning可以较好地发挥作用。 - **SARSA**:更适合于环境中存在一定风险,需要谨慎探索的场景。比如在机器人导航任务中,如果环境中存在障碍物或者危险区域,SARSA可以学习到更加安全可靠的导航策略。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/891174.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
牛客题解 | 斐波那契数列_1
牛客题库题解题目
题目链接
描述
此题是非常经典的入门题了。我记得第一次遇到此题是在课堂上,老师拿来讲“递归”的(哈哈哈)。同样的类型的题还有兔子繁殖的问题。大同小异。此题将用三个方法来解决,从入门到会做。
考察知识:递归,记忆化搜索,动态规划和动态规划的空间…
牛客题解 | 整数中1出现的次数(从1到n整数中1出现的次数)
牛客题库题解题目
题目链接
题目的主要信息:输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数举一反三:
学习完本题的思路你可以解决如下题目:
JZ17. 打印从1到最大的n位数
JZ15. 二进制中1的个数
方法一:按位统计法(推荐使用)
思路:
数字都是由位数组成,某…
牛客题解 | 数组中重复的数字
牛客题库题解题目
题目链接
题目的主要信息:一个长度为\(n\)的数组中只有0到\(n-1\)的数字
需要找出其中任意一个重复出现的数字举一反三:
学习完本题的思路你可以解决如下题目:
JZ56. 数组中只出现一次的两个数字
JZ50. 第一个只出现一次的字符
JZ75. 字符流中第一个不重复…
牛客题解 | 数据流中的中位数
牛客题库题解题目
题目链接
题目主要信息:寻找数据的中位数
数据量在不断输入增长举一反三:
学习完本题的思路你可以解决如下题目:
BM46. 最小的k个数
方法一:插入排序法(推荐使用)
知识点:插入排序
插入排序是排序中的一种方式,一旦一个无序数组开始排序,它前面部分就…
牛客题解 | 数组中出现次数超过一半的数字
牛客题库题解题目
题目链接
题目主要信息:题目给出一个长度为n的数组,其中有一个数字出现次数超过了数组长度的一半,需要我们找出这个数字
输入数组非空,保证有解,这样就不用考虑特殊情况举一反三:
学习完本题的思路你可以解决如下题目:
BM52. 数组中只出现一次的两个数字…
牛客题解 | 数值的整数次方
牛客题库题解题目
题目链接
题目的主要信息:求一个浮点数的整数次方
整数有正有负
不可以使用库函数,也不需要判断大数问题举一反三:
学习完本题的思路你可以解决如下题目:
JZ83. 剪绳子(进阶版)
方法一:直接运算(推荐使用)
思路:
既然是求次方,那我们做不断累乘就可…
支付宝 IoT 设备入门宝典(下)设备经营篇
本篇会以支付宝 IoT 设备经营为中心,介绍常见的设备相关能力和问题解决方案,帮助商户利用设备进行运营动作,让设备更好的帮助自己上篇介绍了支付宝 IoT 设备管理,但除了这些基础功能外,商户还可以利用设备进行一些运营动作,让设备更好的帮助自己,本篇就会以设备经营为中…
国家能源集团某煤矿办公网与工业网整合运维
北京智和信通智和网管平台通过跨网络的整合监控运维能力,对某煤矿中的办公网和工业网进行管理。在一个平台内根据网络类型进行区分管理,统一监控。 国家能源集团某煤矿是国家能源集团在晋陕蒙区域的典型现代化井工煤矿,具有丰富的煤炭资源和先进的生产管理模式。
项目…
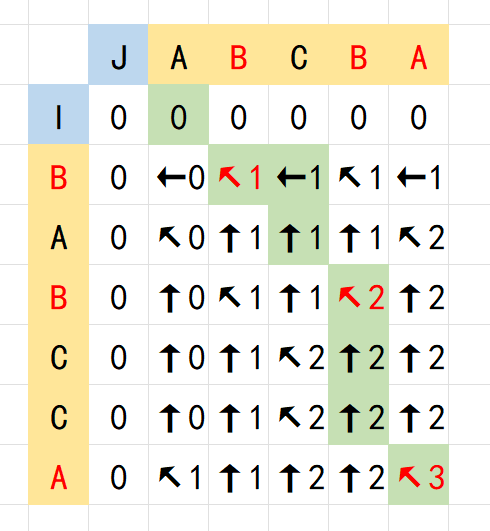
最长公共子序列LCS 笔记
最长公共子序列LCS 笔记
假设存在两个相同长度平凡的序列,我们希望找到它们最长的公共子序列,在没有其他特殊条件的情况下,利用动态规划计算的时间复杂度为 \(O(n^2)\) ,并且可以记录这个子序列
考虑两个指针作用于两个序列上,记 \(dp_{i,j}\) 表示为连续子序列 \([a_1,a_…
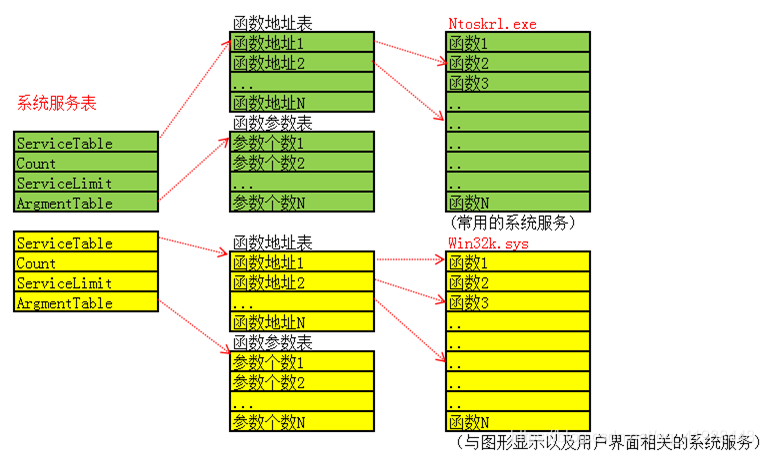
Windows 系统调用学习笔记
依然是 x86 的,照着 lzyddf 师傅的 blog 和 OneTrainee师傅的blog 学的
Windows API
Application Programming Interface,简称 API 函数。Windows API 是微软为 Windows 操作系统提供的一组函数、数据结构、常量和协议,允许开发者与操作系统进行交互。通过 Windows API,开发…
作业一:自我介绍+软工五问
作业一这个作业属于哪个课程
https://edu.cnblogs.com/campus/gdgy/SoftwareEngineeringClassof2023这个作业要求在哪里
https://edu.cnblogs.com/campus/gdgy/SoftwareEngineeringClassof2023/homework/13325这个作业的目标
学习使用github和博客园自我介绍、兴趣爱好
我叫梁鑫…
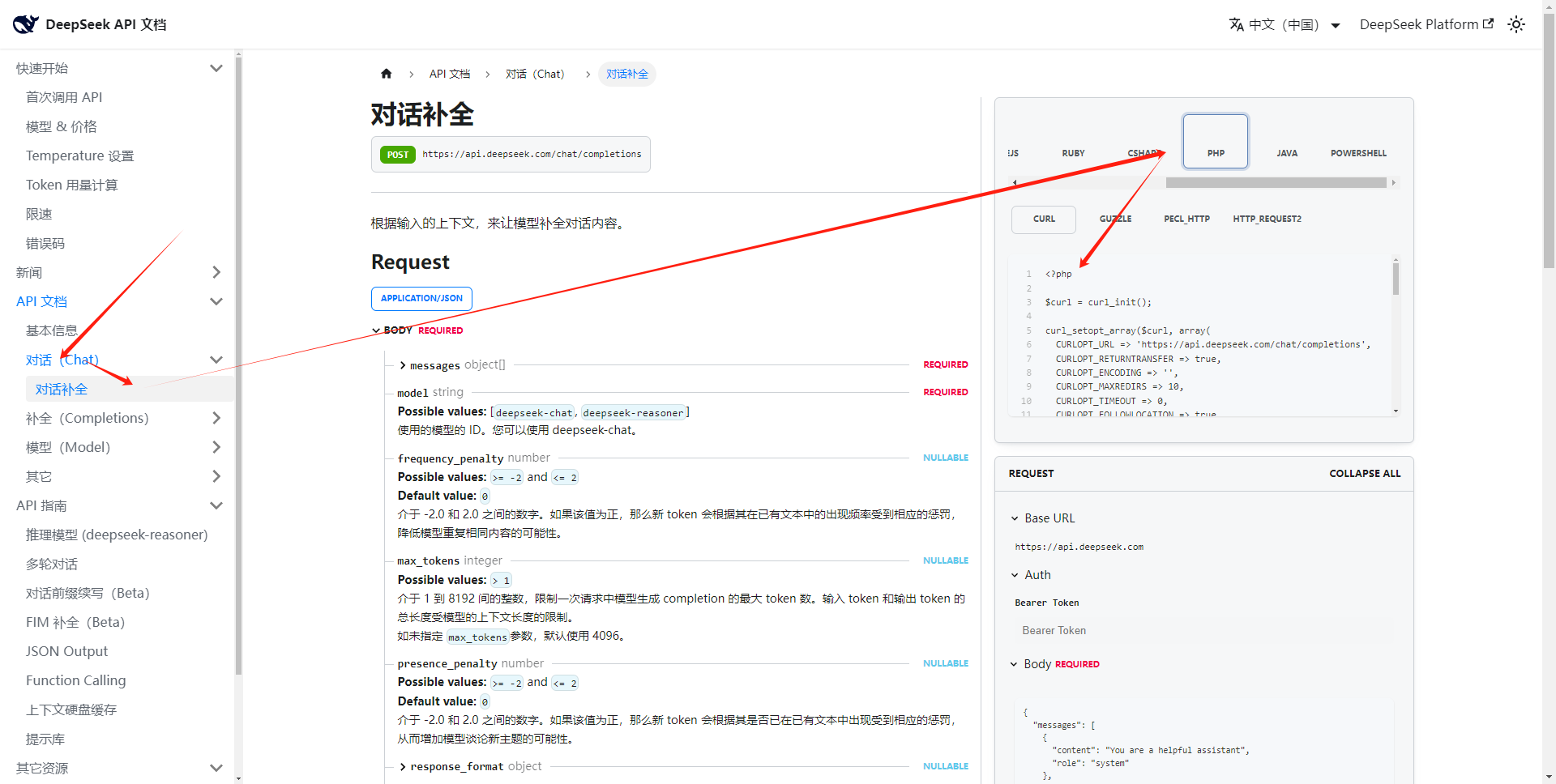
deepseek---官方API接入
最近deepseek又开放充值了,而且还大降价,果断接入:
1、首先就是去充值,然后获取key
2、打开接口文档-找到合适自己的语言接口 3、直接复制代码就能运行<?php$curl = curl_init();curl_setopt_array($curl, array(CURLOPT_URL => https://api.deepseek.com/chat/comp…